角平分线导致的三角形内外角关系
如图(b) ，\(BE\)平分\(\angle ABC\)，\(CE\)平分外角\(\angle ACM\)，试确定\(\angle A\)和\(\angle E\)的数量关系；
如图(c) ，\(BF\)平分外角\(\angle CBP\)，\(CF\)平分外角\(\angle BCQ\)，试确定\(\angle A\)和\(\angle F\)的数量关系；
解析：如图(a)，延长 \(BD\) 交 \(AC\) 于\(H\)，则\(\angle BDC=\angle BHC+\angle DCH\)，
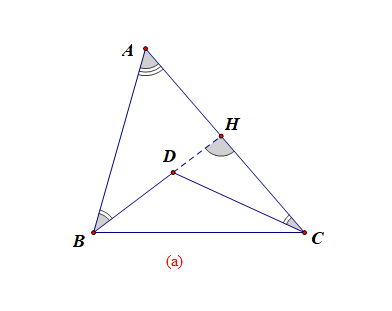
又由于\(\angle BHC=\angle A+\angle HBA\)，
则\(\angle D=\angle BDC=\angle A+\angle HBA+\angle DCH\)
又由于\(\angle HBA=\cfrac{1}{2}\angle B\)，\(\angle DCH=\cfrac{1}{2}\angle C\)，
故\(\angle BDC=\angle A+\cfrac{1}{2}(\angle B+\angle C)\)，
即\(\angle BDC=\angle A+\cfrac{1}{2}(180^{\circ}-\angle A)\)，
故\(\angle BDC=90^{\circ}+\cfrac{1}{2}\angle A\)；
即\(\angle D=90^{\circ}+\cfrac{1}{2}\angle A\)；
如图(b)，由于\(\angle ACM=\angle A+\angle B\)，
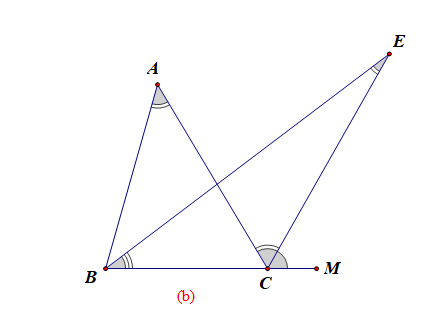
又\(\angle ECM=\cfrac{1}{2}\angle B+\angle E\)，
则\(\cfrac{1}{2}\angle ACM=\cfrac{1}{2}\angle A+\cfrac{1}{2}\angle B\)，
又由于\(\angle ECM=\cfrac{1}{2}\angle ACM\)，
则\(\cfrac{1}{2}\angle B+\angle E=\cfrac{1}{2}\angle A+\cfrac{1}{2}\angle B\)，
故\(\angle E=\cfrac{1}{2}\angle A\)；
如图(c)，由于\(\angle CBF+\angle FBC+\angle F=180^{\circ}\)，
即\(\cfrac{1}{2}(180^{\circ}-\angle ABC)+\cfrac{1}{2}(180^{\circ}-\angle ACB)+\angle F=180^{\circ}\)，
整理得到，\(\angle F=\cfrac{1}{2}(\angle ABC+\angle ACB)\)，
即\(\angle F=\cfrac{1}{2}(180^{\circ}-\angle A)=90^{\circ}-\cfrac{1}{2}\angle A\)；
