求一次函数解析式

前言

一次函数的解析式形式为\(y=kx+b(k\neq0)\)，由于我们都知道其形式，故求解一般都是待定系数法；此时只要知道两个点的坐标，代入得到方程组，解方程组即可；

如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中,路程随时间变化的图像（分别是正比例函数图像和一次函数图像）

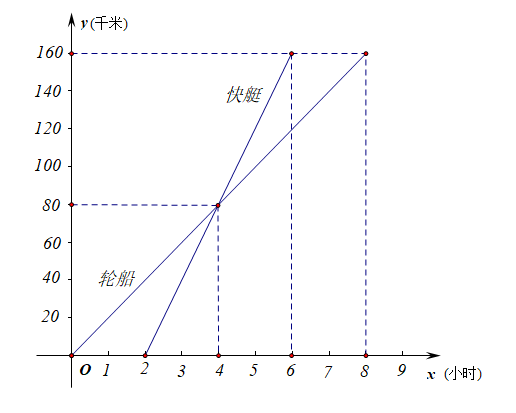
求解：（1）分别写出轮船和快艇随时间变化的函数表达式.

解析：由图可知，轮船和快艇随时间变化的图像都是直线，故可知其函数解析式为一次函数型；

设轮船的函数表达式为\(y=k_1x(k_1\neq0)\)，

由于其经过点\((4,80)\)，代入得到\(80=4k_1\)，

解得\(k_1=20\)，故轮船的函数表达式为\(y=20x(0\leqslant x\leqslant 8)\)，

设快艇的函数表达式为\(y=k_2x+b(k_2\neq0)\)，

由于其经过点\((2,0)\)，\((4,80)\)，代入得到\(\left\{\begin{array}{l}{2k_2+b=0}\\{4k_2+b=80}\end{array}\right.\)

解得\(k_2=40\)，\(b=-80\)

故快艇的函数表达式为\(y=40x-80(0\leqslant x\leqslant 8)\).

（2）经过多长时间,快艇和轮船相距20千米?

解：由(1)可知，轮船和快艇随时间的路程表达式分别为\(y=20x\)，\(y=40x-80\)，

[当我们不知道谁快谁慢的时候，我们可以用二者的差的绝对值]，故有

\(|20x-(40x-80)|=20\)，整理为\(|20x-80|=20\)，

即\(20x-80=20\)或\(20x-80=-20\)，

解得\(x=3\)或\(x=5\)，

故刚好经过三小时，轮船与快艇相距\(20\)千米，此时轮船比快艇快；

刚好经过五小时，快艇与轮船相距\(20\)千米，此时快艇比轮船快；

[难点]如图所示，在平面直角坐标系\(xOy\)中，直线\(AB\)与\(x\) 轴与\(y\) 分别交于点\(A(3,0)\)，\(B(0,4)\)，点\(C\)在\(y\) 轴的负半轴上，若将\(\triangle CAB\)沿直线\(CA\)折叠，点\(B\)恰好落在\(x\) 轴的正半轴的点\(D\)处.

(1).直接写出线段\(AB\)的长度；

分析：\(AB=\sqrt{3^{2}+4^{2}}=5\)，故答案为： \(5\)；

(2).求直线\(AB\)的函数表达式；

分析：将点 \(A\) 、\(B\) 的坐标代入一次函数表达式： \(y=k x+b\)，并解得：直线 \(AB\) 的表达式为： \(y=-\cfrac{4}{3}x+4\)；

(3).求点\(D\)和点\(C\)的坐标；

分析：由题意得: \(AD=AB=5\)， 故点\(D(8,0)\)，

设点 \(C\) 的坐标为 \((0, m)\)， 而 \(CD=BC\)， 即\(4-m=\sqrt{m^{2}+8^{2}}\)，解得: \(m=-6\)，故点 \(C(0,-6)\)；

(4).\(y\) 轴上是否存在一点\(P\) ，使得\(S_{\triangle PAB}=\cfrac{1}{2}S_{\triangle OCD}\)， 若存在，直接写出点\(P\)的坐标；若不存在，请说明理由.

分析：设点 \(P(0, n)\)，则由\(\cfrac{1}{2}S_{\triangle OCD}=\cfrac{1}{2} \times \cfrac{1}{2} \times CO \times OD=\cfrac{1}{4} \times 6 \times 8=12\)

\(S_{\triangle ABP}=\cfrac{1}{2}BP\times x_{A}=\cfrac{1}{2}\times|4-n|\times 3=12\)，解得： \(n=12\) 或 \(-4\)，

故所求点的坐标为\(P(0,12)\)或\(P(0,-4)\).