尺规作图
前言
相关定义
尺规作图(Compass-and-straightedge construction)是指用没有刻度的直尺和圆规作图。最基本,最常用的尺规作图,通常称基本作图。一些复杂的尺规作图都是由基本作图组成的。
基本作图
以下是最基本最常用的尺规作图,需要重点理解和掌握;
1、作一条线段等于已知线段;
2、作一个角等于已知角;
3、作已知线段的垂直平分线;
4、作已知角的角平分线;
5、过一点作已知直线的垂线;
经典操作
九大经典操作,需要重点理解和掌握;
(1)题目一:作一条线段等于已知线段。
已知:如图,线段\(a\).
求作:线段\(AB\),使\(AB\)=\(a\).
作法:
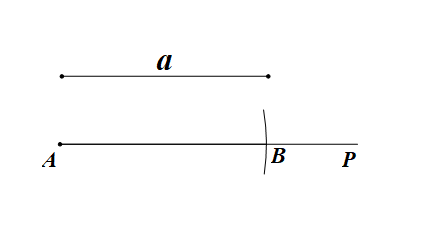
①.作射线\(AP\);
②.在射线\(AP\)上截取\(AB=a\).
则线段\(AB\)就是所求作的图形。
(2)题目二:作已知线段的垂直平分线。
已知:如图,线段\(MN\).
求作:线段\(PQ\),使\(PQ\perp MN\)且\(PQ\)平分线段\(MN\).
作法:
①. 分别以\(M\)、\(N\)为圆心,大于\(\cfrac{1}{2}MN\)的相同线段为半径画弧,两弧相交于\(P\),\(Q\);
②. 连接\(PQ\)交\(MN\)于\(O\).
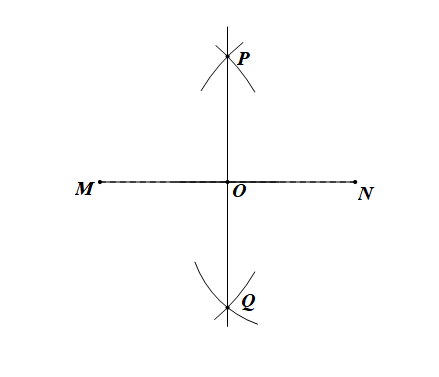
则线段\(PQ\)就是所求作的\(MN\)的垂直平分线。
(3)题目三:作已知角的角平分线。
已知:如图,已知\(\angle AOB\),
求作:射线\(OP\),使\(\angle AOP=\angle BOP\),(即\(OP\)平分\(\angle AOB\))。
作法:①.②.③.④.⑤.
①.以\(O\)为圆心,任意长度为半径画弧,分别交\(OA\),\(OB\)于\(M\),\(N\);
②.分别以\(M\)、\(N\)为圆心,大于\(\cfrac{1}{2}MN\)的线段长为半径画弧,两弧交\(\angle AOB\)内于\(P\);
③.作射线\(OP\)。
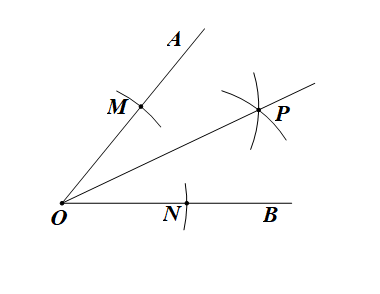
则射线\(OP\)就是\(\angle AOB\)的角平分线。
(4)题目四:作一个角等于已知角。
已知:如图,已知\(\angle AOB\),
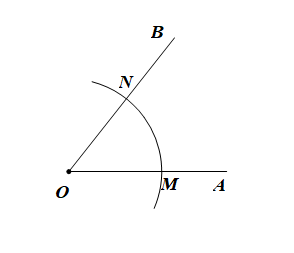
求作:\(\angle A'O'B'\),使得\(\angle AOB=\angle A'O'B'\),
作法:
①.作射线\(O'A'\);
②.以\(O\)为圆心,任意长度为半径画弧,交\(OA\)于\(M\),交\(OB\)于\(N\);
③.以\(O'\)为圆心,以\(OM\)的长为半径画弧,交\(O'A'\)于\(M'\);
④.以\(M'\)为圆心,以\(MN\)的长为半径画弧,交前弧于\(N'\);
⑤.连接\(O'N'\)并延长到\(B'\)。
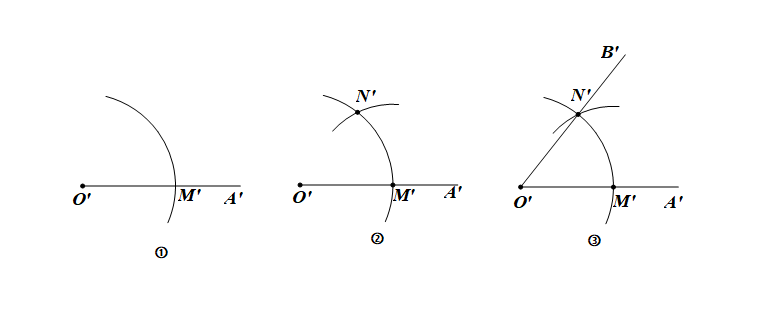
则\(\angle A'O'B'\)就是所求作的角。
(5)题目五:经过直线上一点做已知直线的垂线。
已知:如图,\(P\)是直线\(AB\)上一点。
求作:直线\(CD\),使得\(CD\)经过点\(P\),且\(CD\perp AB\)。
作法:
①.以\(P\)为圆心,任意长为半径画弧,交\(AB\)于\(M\)、\(N\);
②.分别以\(M\)、\(N\)为圆心,大于\(\cfrac{1}{2}MN\)的长为半径画弧,两弧交于点\(Q\);
③.过\(D\)、\(Q\)作直线\(CD\)。
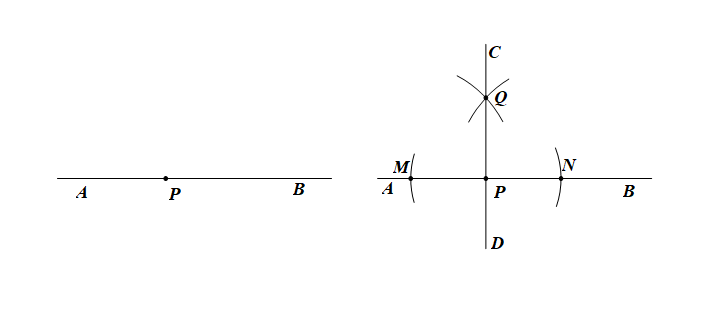
则直线\(CD\)是求作的直线。
(6)题目六:经过直线外一点作已知直线的垂线
已知:如图,直线\(AB\)及直线外一点\(P\)。
求作:直线\(CD\),使\(CD\)经过点\(P\),且\(CD\perp AB\)。
作法:
①.以\(P\)为圆心,以大于点\(P\)到直线\(AB\)的距离为半径画弧,交\(AB\)于\(M\)、\(N\);
②.分别以\(M\)、\(N\)圆心,大于\(\cfrac{1}{2}MN\)的长为半径画弧,两弧交于点\(Q\);
③.过\(P\)、\(Q\)作直线\(CD\)。
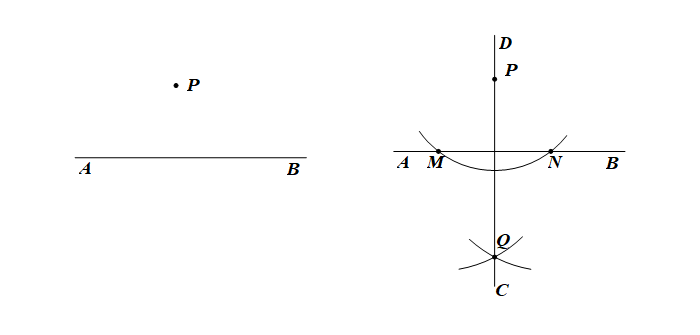
则直线\(CD\)就是所求作的直线。
(7)题目七:已知三边作三角形。
已知:如图,线段\(a\),\(b\),\(c\).
求作:\(\triangle ABC\),使\(AB=c\),\(AC=b\),\(BC=a\).
作法:
①.作线段\(AB=c\);
②.以\(A\)为圆心,以\(b\)为半径作弧,以\(B\)为圆心,以\(a\)为半径作弧与前弧相交于\(C\);
③.连接\(AC\),\(BC\)。
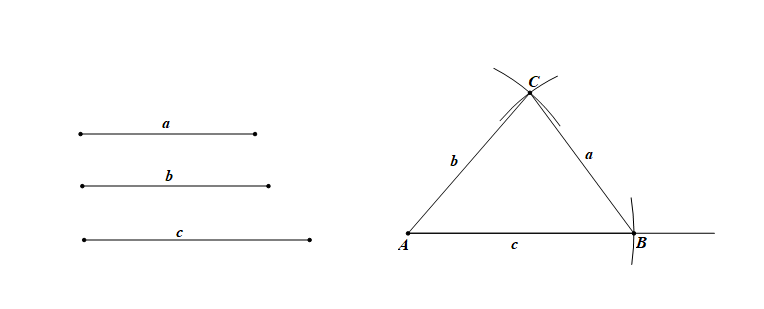
则\(\triangle ABC\)就是所求作的三角形。
(8)题目八:已知两边及夹角作三角形。
已知:如图,线段\(m\),\(n\), \(\angle\alpha\).
求作:\(\triangle ABC\),使\(\angle A=\angle\alpha\) ,\(AB=m\),\(AC=n\).
作法:
①.作\(\angle A=\angle\alpha\);
②.在\(AB\)上截取\(AB=m\),\(AC=n\);
③.连接\(BC\)。
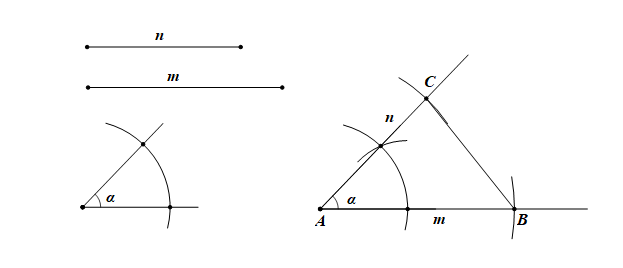
则\(\triangle ABC\)就是所求作的三角形。
(9)题目九:已知两角及夹边作三角形。
已知:如图,\(\angle\alpha\),\(\angle\beta\),线段\(m\).
求作:\(\triangle ABC\),使\(\angle A=\angle\alpha\),\(\angle B=\angle\beta\),\(AB=m\).
作法:
①.作线段\(AB=m\);
②.在\(AB\)的同旁作\(\angle A=\angle\alpha\),作\(\angle B=\angle\beta\),\(\angle A\)与\(\angle B\)的另一边相交于\(C\)。
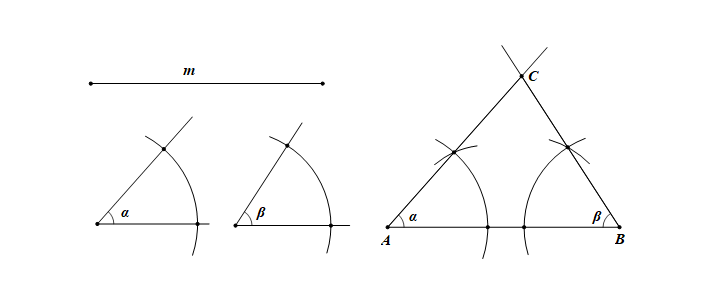
则\(\triangle ABC\)就是所求作的三角形。
典例剖析

分析:本题目就是求作\(\angle AOB\)的角平分线和线段\(CD\)的垂直平分线的交点;
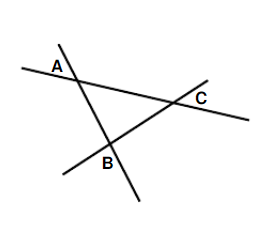
分析:本题目就是求作内角的角平分线的交点(或三角形的内心)和外角的角平分线的交点;

由于\(\triangle ABC\)内角平分线的交点到三角形三边的距离相等,则\(\triangle ABC\)内角平分线的交点满足条件;
如图:点\(P\)是\(\triangle ABC\)两条外角平分线的交点,过点\(P\)作\(PE⊥AB\),\(PD⊥BC\),\(PF⊥AC\),
由于\(PE=PF\),\(PF=PD\),则有\(PE\)\(=\)\(PF\)\(=\)\(PD\),
所以点\(P\)到\(\triangle ABC\)的三边的距离相等,
所以\(\triangle ABC\)两条外角平分线的交点到其三边的距离也相等,满足这条件的点有\(3\)个;
综上,到三条公路的距离相等的点有\(4\)个,故可供选择的地址有\(4\)个.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号