MP and OMP

MP

Given $f$ and a set of vectors $G=\{g_{\gamma}\}$, We want to find some atoms in $G$ to linearly represent $f$, i.e.,

$$f=a_1 g_1+a_2g_2+\cdots+a_ng_n+\epsilon_n.$$

If we define $R^0f:=f$, We can realize this in a recursive manner, like the way

$$R^0f=a_1g_1+R^1f$$

and 

$$R^1f=a_2g_2+R^2f$$

and so on, then after $n$ steps, we can obtain

$$R^0f=a_1g_1+\cdots+a_ng_n+R^{n}f.$$

The success to this procedure relies on the remainder to be decreasing in some way. The key to guarantee this is othogonal decomposion theorem. That is at every step, we choose atom to satisfy 

 

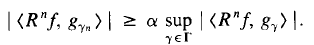
where $0<\alpha\leq 1$, idealy it is chosen as 1. Then we apply othogonal decomposition as  $R^{n-1}f=a_ng_n+R^nf$ and $R^nf \perp g_n$. Moreover, the Pythagoras's theorem stands

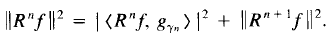
as well as the energy conservation law

 

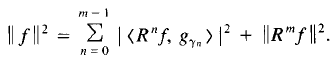
OMP

 As can be seen from the MP procedure, at each iteration, we only have a local orthogonal projection property, i.e, 
$R^{n}f \perp g_{\gamma_n}$. So the finite steps convergence is lost. A remedy to this is to enforce more orthogonal constraints, like OMP algorithm,

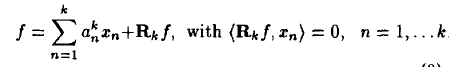
 This is just a linear systems, which can be solved by pysudo-inverse of the coefficient matrix. Also,using matrix inversion lemma, it can be solved in a recursive way, see the reference by P.C,Pati et al(1993).