Lagrange Dual Theory for NLP

1. Classic form of nonlinear programming
   F1: \(f,h,g\) are arbitrary (not necessarily diferentiable or continuous) functions.
   
   F2:
   
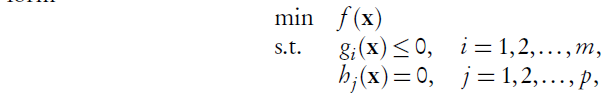
   F3:

\[\begin{align*} \min \; & f(x)\\ \textrm{s.t.} \; & g(x)\leq 0\\ & h(x)=0 \\ & x\in X; \end{align*}\]

As \(h(x)=0\) can be equivalently written as two inequality constraints \(h(x)\leq 0\) and \(-h(x)\leq 0\), we only consider

\(\color{red}{\mbox{Denote the primal domain by}}\) \(D=X\cap \{x|g(x)\leq 0, h(x)=0\}\).}

2. Lagrange function and its dual

1. Lagrange function:\(\mu \geq 0\) is called the Lagrange multiplier.
   
   2)Lagrange dual function
   
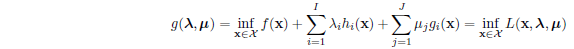
   [Remark]Observe that the minimization to calculate the
   dual is carried out over all \(x \in X\), rather than just those within the constraint set. For this reason, we can prove that for primal feasilbe \(x\in D\) and dual feasible \((\lambda, \mu \geq 0)\) , we have

\[g(\bar{\lambda},\bar{\mu})\leq f(\bar{x}) \]

So we have for \(\mu \geq 0\) and \(x\in D\),

\[d^*=\sup g(\lambda,\mu)\leq \inf f(x)=f^*$$, which is called weak dual theorem. 3. Weak duallity    If strong duality holds, then optimal pair $(x,\lambda,\mu)$ must satisfy the KKT conditions. $$\mbox{An optimal solution geometric multiplier pair} \Leftrightarrow \mbox{Dual gap=0} \Leftrightarrow \mbox{Saddle point theorem} \]

\[\Leftrightarrow \]

\[\Rightarrow \mbox{KKT conditions} \]

If primal is convex optimization, then KKT is sufficient.

4. Strong Duality: convex optimization with slater condition
   \(f, g\) is convex, \(h\) is affine and there exists point \(x\) in relative interior of the constraint set such that all of the (nonlinear convex) inequality constraints hold with strict inequality.
   In such case, dual gap disappeared and the KKT conditions are both necessary and sufficient for \(x\) to be the global solution to the primal problem.

5. Saddle point and dualilty gap
   
   
   
   

6. Saddle point and KKT condtions
   
   
   \(\color{red}{\mbox{Remark:}} \mu^Tg(x)=0\) and \(g(x)\leq 0\) and \(\mu\geq 0\) means \(\alpha_i g_i=0\).

7. KKT point is optimizer when dealing with convex ptimization
   Any point which satisfies KKT conditions is an optimizer when dealing with a convex problem no matter Slater's holds or not but if it holds, an optimizer must hold the KKT conditions.