图论的小技巧以及扩展
图论,其实是数学的一门分支,它以图为研究对象。最基础的图论应该是著名的哥尼斯堡七桥问题,那是一个经典的一笔画问题。
竞赛中我们比较常见的是 最短路算法 最小生成树算法 拓扑排序 等等。
本篇文章我们不说那些大家都懂烂了的图论算法,讲一些实用的 (没什么用的) 图论小技巧。
链式前向星存图
最最基础的存图的基本分为两种,使用二维数组和使用 \(vector\) ,但这两种方法都有所缺陷。
使用二维数组查询速度很快,但空间复杂度是 \(O(n^2)\) 的,一般的题目都接受不了。
使用 \(vector\) 可以减少空间复杂度,但是时间就比较不确定了。
所以就出现了一种神奇的存图方式,链表思想的链式前向星。
我们通常使用以下数组来完成
$Codes$
int w[i]//第 i 条边的权值
int to[i]//第 i 条边的终点
int nxt[i]//下一条的边的编号,不建议叫 next,会挂
int head[i]//以 i 为起始点的第一条边
int tot//边的编号
新增加一条边的时候我们进行如下操作
$Codes$
void add(int x,int y,int z){
tot++;//新边的编号
to[tot]=y;//新一条边的信息
w[tot]=z;
nxt[tot]=head[x];
head[x]=tot;//更新以 x 为起始点的第一条边
}
//这样是单向边,双向边要再来一次
用下面这种方式就可以枚举出所有以 xx 为起始点的边。
$Codes$
for(int i=head[x];i;i=nxt[i]){// i 即为该边编号
//to[i]为可以到达的点头
//w[i]为这条边的权值
}
大致思想就是将所有以 \(x\) 为起始点的边以链表的形式储存,枚举的时候遍历链表,直到边的编号为 \(0\) (为 \(0\) 表示没有其他的边了)
这样就可以满足我们从某个点遍历枚举下个点的需要。
前向星链表被疯狂应用在各个图论题目中,基本上是一个图论题都可以用到吧,属于非常基础的图论技能。
需要注意的是对于双向边的题目,链式前向星的数组需要开边数的两倍,不然会 \(RE\) 。
反向建边
对于一个有向图,某些问题中我们需要反向建边来完成操作
比如求其他 \(n\) 个点到 \(k\) 点的最短路。
对每个点跑一遍最短路不就好了吗?
事实上我们只需要跑一遍最短路就可以了,只需要把边反向建。
反向建图情况下 \(k\) 点到每个点的最短路就是正常情况下该点到 \(k\) 点的最短路。
例题 P1629 邮递员送信
不只是最短路问题,在遍历问题上也可以使用反向建边来完成
例题 P3916 图的遍历
是否需要反向建边,根据题意判断即可。
反向建边还可以来判断某条边是否在最短路上。
对于一个有向图,我们从 11 号点跑一遍正向的最短路 \(dis[]\) ,从 \(n\) 号点跑一遍反向的最短路 \(dis1[]\)
如果 \(dis[x]+w(x,y)+dis1[y]=dis[n]\) 那么我们就可以得出,这条边是在 \(1\) 到 \(n\) 的最短路上的。
当然如果是无向图的话直接跑就可以了。
虚点连边
虚点连边是一种很有效的优化建边复杂度的方式
我们可能会遇见这样一种题,给你几个点,其他的点离这些给出的点的最近距离是多少。
我们可以对于每一个点进行 \(Spfa\),但似乎这样并不是很好操作。
我们可以自己给出一个点,然后向每个被标记的点连一条单向边,这样就只需要进行一次 \(Spfa\) 就可以了。
举个例子,橙色为标记点,数字为最近距离。
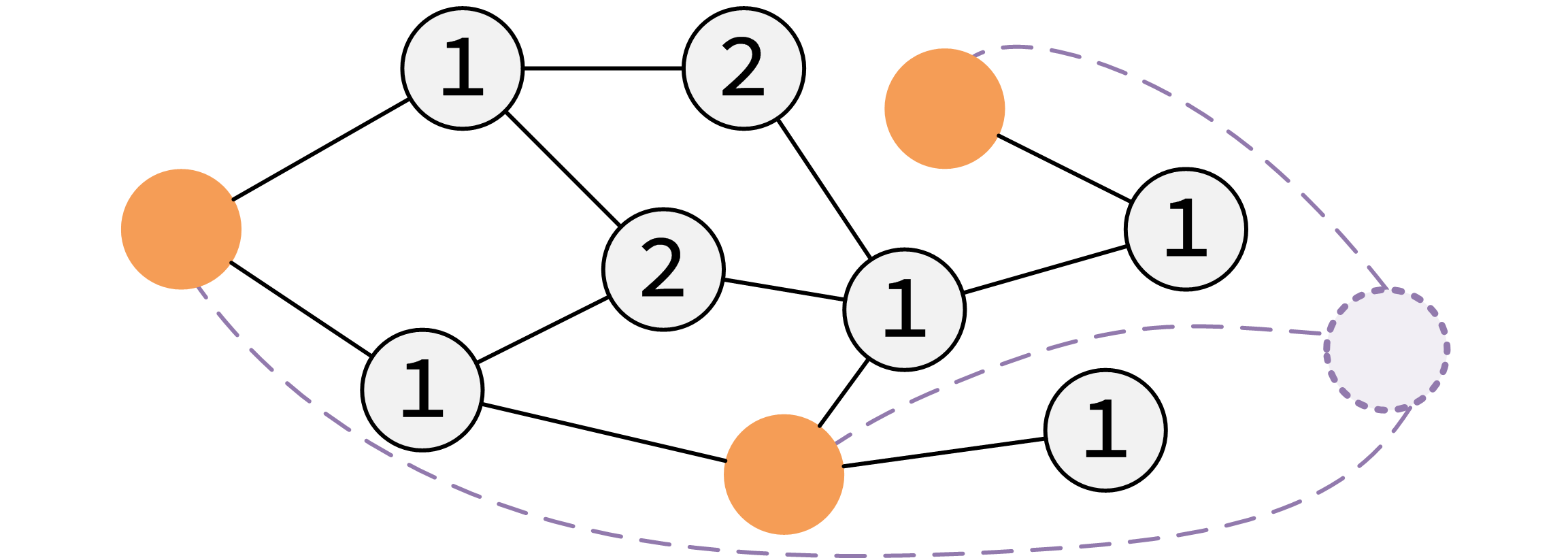
例题 P3393 逃离僵尸岛
但似乎这个直接广搜也可以。
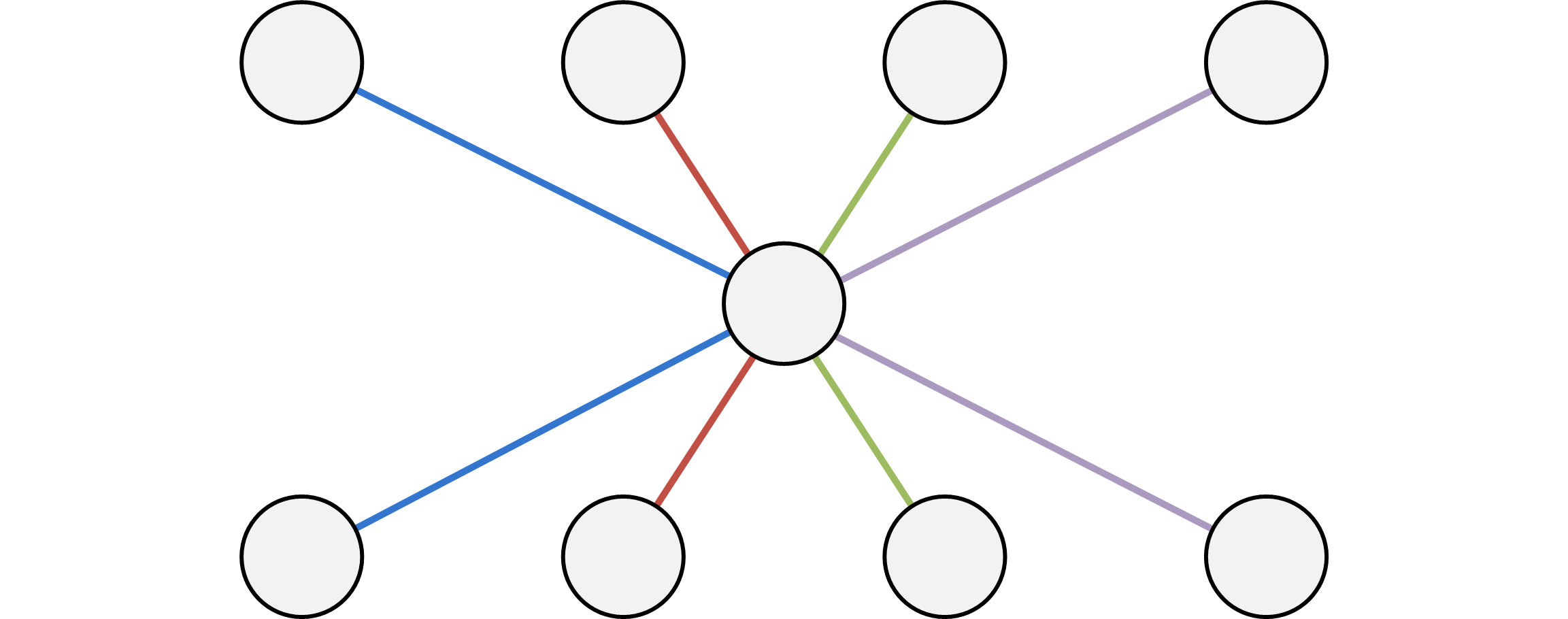
如果对于两个点集 \(A\) 和 \(B\),你需要对 \(A\) 中的每一个点向 \(B\) 中的每一个点都建一条边,如果直接操作,复杂度很明显是 \(O(n^2)\) 的,有没有更快的方法呢?
我们可以建一个虚点 \(P\) ,然后对 \(A\) 里的每一个点向 \(P\) 连一条单向边边,然后对 \(P\) 向 \(B\) 中的每一个点建一条单向边,这样只需要 \(O(2n)\) 的复杂度就可以完成了。
画个图理解一下。
(优化前)
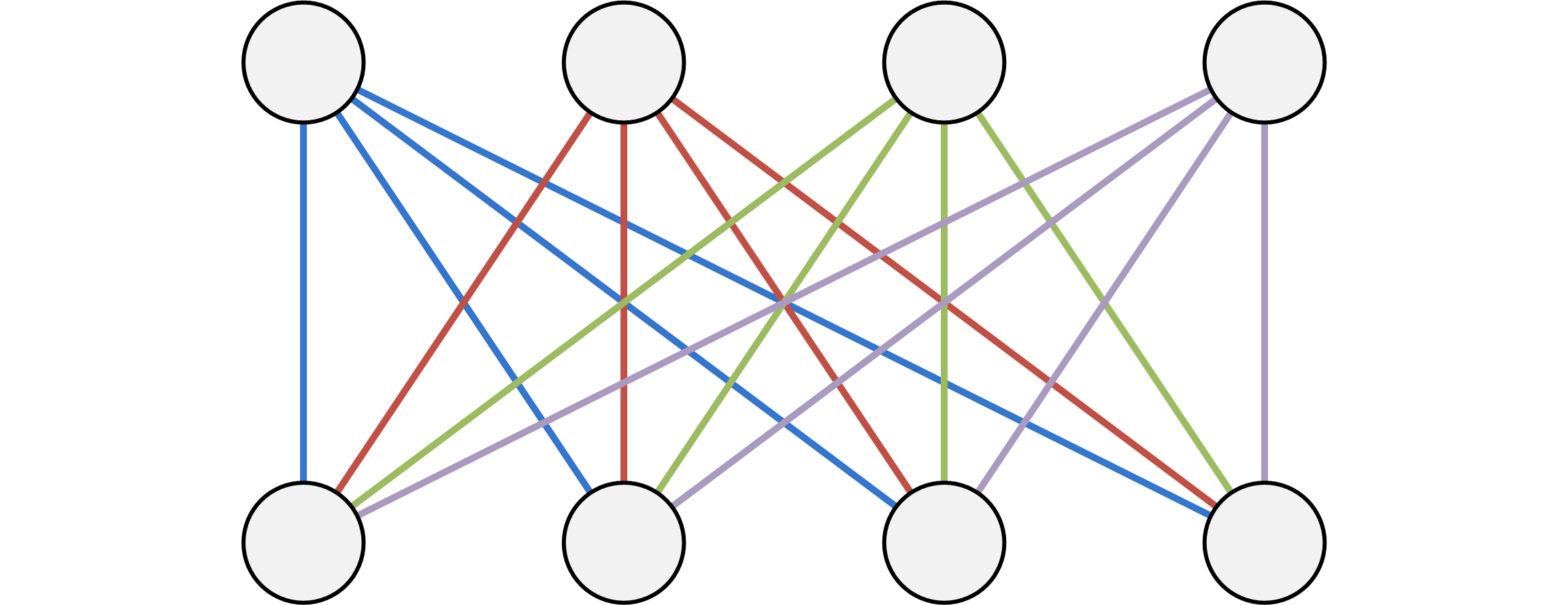
(优化后)
例题 P1983 车站分级
虚点连边只是听起来很高大上的操作,但实际上很简单。
对于有边权的情况,虚点连得边的边权需要注意(一般为 \(0\) )
线段树优化建边
说到优化建边,就一定要介绍一下线段树优化建边了。
这也是一个听起来非常高大上但实际上不是很难的技巧。
给你一个点 \(X\) ,让你和一个点集里的每一个点都连一条边。看起来并没有什么好方法,只能乖乖地一个一个连
如果这个点集是连续的呢?我们就可以用线段树来优化建边了。
我们知道线段树是这个结构的
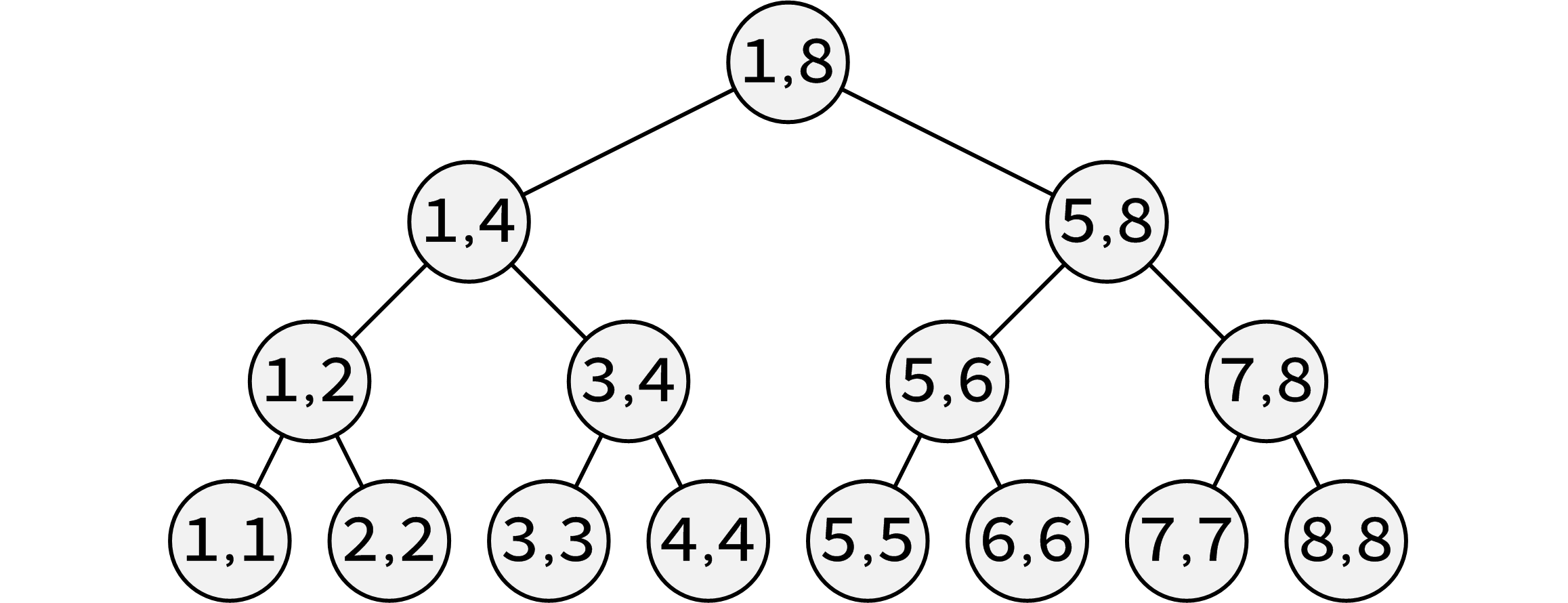
我们知道,线段树的点是能够代表一段区间的,那么我们怎样应用这个性质呢?
首先,我们需要对于线段树的每个父亲与他的儿子建一条单向边,效果如下
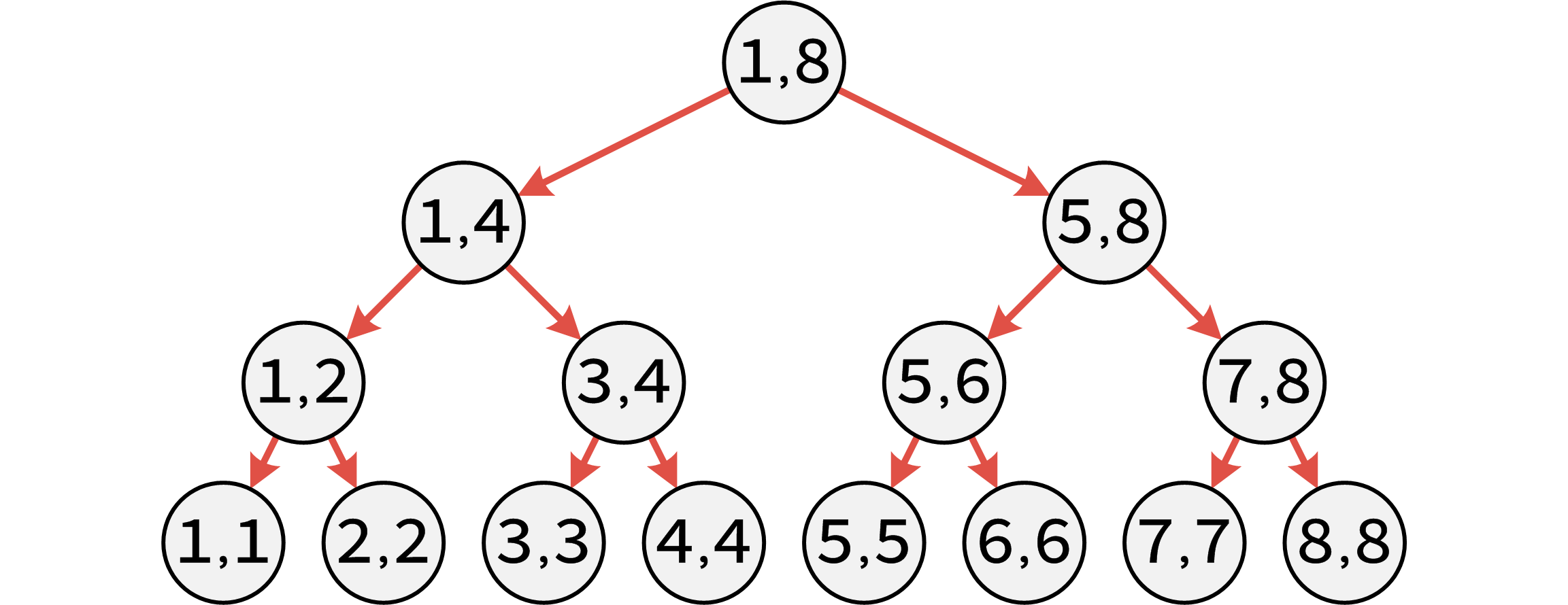
这有什么用呢?因为我们所要求的点集是一段连续的区间,而线段树的结点可以表示某一段区间,我们可以在线段树上找到对应的区间,然后向线段树上的点建边,就可以加快建边速度了。
例如我们要向 \([1,8]\) 里的所有点建边,我们只需要将 \(X\) 和线段树上 \([1,8]\) 那个点连一条单向边就可以了。
\([2,6]\) 的例子
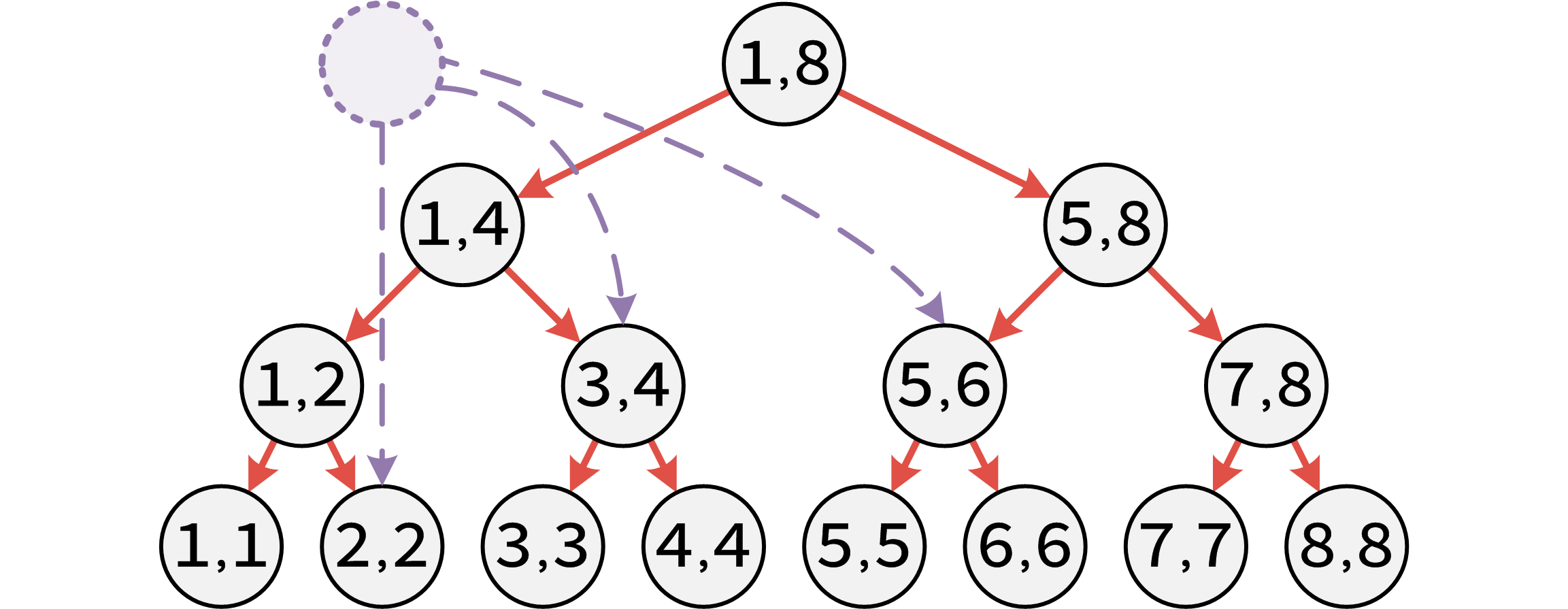
我们在线段树上的边边权一般都是 \(0\) ,边权直接赋给 \(X\) 连到线段树上的那条边即可
建树和寻找的代码和普通线段树差不多。需要注意的是线段树上结点的编号不要和已有的点重复,最后的结点直接连上该点就好。
$Codes$
void build(int &p,int l,int r){
if(l==r){
p=l;
return ;
}
p=++cnt;//点的编号
int mid=l+r>>1;
build(lc[p],l,mid);build(rc[p],mid+1,r);
add(lc[p],p,0);add(rc[p],p,0);
}
void update(int p,int l,int r,int x,int L,int R,int z){
if(L<=l && r<=R){
add(x,p,z);
return ;
}
int mid=l+r>>1;
if(L<=mid){
update(lc[p],l,mid,x,L,R,z);
}
if(R>mid) {
update(rc[p],mid+1,r,x,L,R,z);
}
}
这道题还涉及到了区间向某一个点连边的情况,我们再建一个棵线段树在树上反向建边就可以了
拆点构图
有些时候我们并不能用一个点来代表一个点(雾)
诶我不是这个意思。我的意思是用几个点来表示一个点的不同情况。
随机口胡的一道题
一个图,每条边上有 \(k\) 个权值,第 \(i\) 次行走消耗的代价是第 \(i\%k+1\) 个权值,求某一个点的单源最短路径。 \(( k\)很小\()\)
看起来直接跑 \(dij\) 和 \(spfa\) 是不对的,可以自举反例。
可以使用 \(dfs\) ,用 \(dis[i][j]\) 表示到第 \(i\) 个点走了 \(m\) 步且 \(m\%k+1=j\) 的最短方案,但这样太慢了。
我们可以使用拆点的思想,对于一个点 \(i\) ,将它拆为 \(i , i+n , i+2*n , ...\) 这样的 \(k\) 个点,作为到这个点的步数模 \(k\) 不同情况的替代点。
然后我们连边的时候对某一种情况赋不同情况的权值,大概下面这样?
//我们要对 x 到 y 连三种边 w1 w2 w3
add(x,y+n,w1);
add(x+n,y+2*n,w2);
add(x+2*n,y,w3);
来一张图
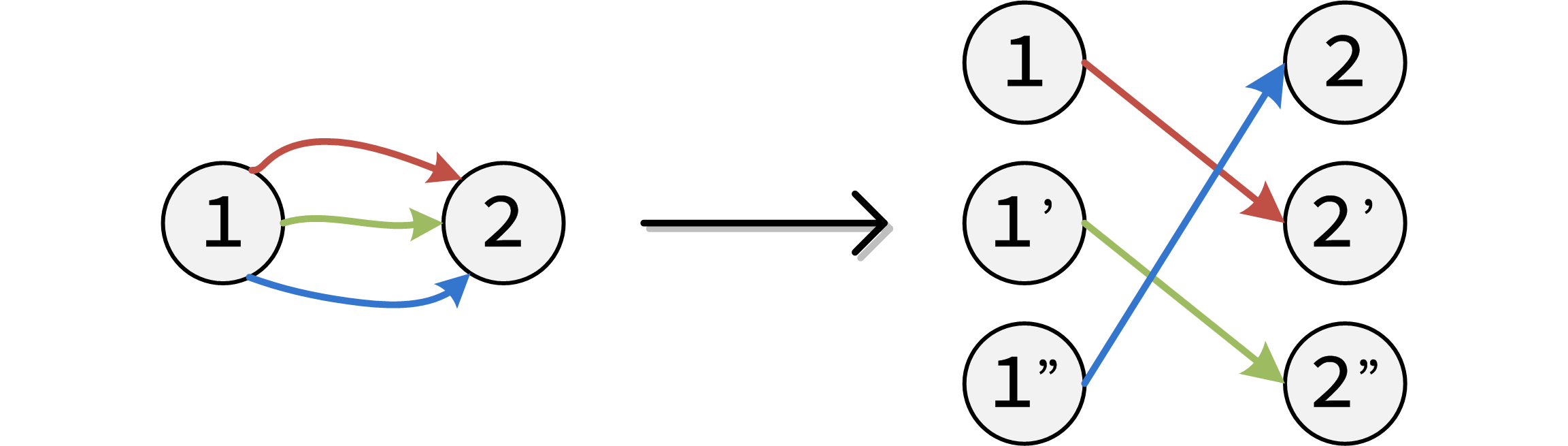
然后在得到的图上跑最短路就可以了,答案要枚举到终点的情况。
类似的例题 P4568 飞行路线
图论建模
似乎……一些背包问题可以用最短路解决,只是没什么必要。
\(Let us AC it--\)题面
\(Kodak\)开了一家小店赚外快,因为店小,所以只有 \(n\) 种不同价格的商品卖,不过好在批发商给力,货源充足,所以每种商品都有无限件。
因为各种原因,有时候顾客会对购买的总价有特殊的要求,比如计算机科学家泰玛仕一定要总价 \(1024\) ,给小姐姐买礼物的面包需要总价 \(520\) 或者 \(1314\) ,或者纯粹来找茬的张三要买\(0\)元商品
但是\(Kodak\)店里不一定有 \(1\) 元的商品,所以并不是所有价格都凑得出来,所以他需要一个程序解决能知道某一个总价能否凑出
看起来可以用完全背包解决这个问题,但是这道题的数据范围不太友好。
商品数 \(N <= 1000\) \ 商品价格 \(a_i <= 20000\)
顾客数 \(M <= 300000\) \ 需求价格 \(b_i <= 40000000\)
如果打完全背包,复杂度会爆炸。\(TAT\)
其实这个问题就是 \(a_1*x_1+a_2*x_2+a_3*x_3+...?=k\) 的问题。我们考虑 \(“\)同余 \(+\) 最短路\(”\)
依题意得,如果 \(k\) 满足要求,那么 \(a_m*k\) 必定也满足条件。我们可以先给它填一堆 \(a_m\) ,然后减去 \(p\) 个 \(a_m\) ,用剩下的 \(a_i\) 表示 \(p*a_m+k\%a_m\) 设当 \(b\%a_m=i\)时,需要的最小的 \(k×a_m+i\) 为 \(dis[i]\) ,剩下的即可用最短路的思想来更新,
跑最短路的过程基本如下
memset(dis,0x3f,sizeof(dis));
dis[0]=0;
q.push(0);
while(q.size()){
int x=q.top();
q.pop();
if(v[x]) continue;
v[x]=1;
for(int i=1;i<=n;i++){
int y=(x+a[i])%mod;
if(dis[y]>dis[x]+a[i]){
dis[y]=dis[x]+a[i];
q.push(y);
}
}
}
可能不是太好理解,结合样例手推一下吧
又一道例题
给出 \(n\) 个 长度为 \(m\) 的 \(01\) 串,让你确定一个长度相同的 \(01\) 串,该串和给出的串中不同的位数最多。
一道看起来跟图论毫无关系的题,其实也可以当作图论来做
我们可以建一个 \(2^m\) 的图,每个点都与和自身不同位数为 \(1\) 的点连一条长度为 \(1\) 的边,然后跑 \(bfs\),得到最远距离的那个点即为所求。
广搜代码
while(h<=t){
int x=v[h];
for(int i=1;i<=m;i++){
int z=x^(1<<(i-1));
if(f[z]==0){
f[z]=1;
t++;
v[t]=z;
dis[z]=dis[x]+1;
}
}
h++;
}
这有点类似于前面讲的虚点连边的那道题。
我讲的可能比较菜,可以画图理解。
图论中要注意的坑
简单列述几个小问题
\(1.\) 先看眼是有向图还是无向图,无向图数组开两倍。
\(2.\) 如果题目中没有声明无自环和重边,需要注意
\(3.\) 有些遍历的题要考虑环,否则可能死循环,可以使用缩点
\(4.\) 如果题目中边权小于等于零,要考虑负环、零环的情况
\(5.\) 跑最短路的时候要赋初值。
\(6.\) 关于 \(Spfa\) ,能不用还是不用吧,毕竟容易被卡。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号