「IOI2017」接线 的另类做法
看到这题,我的第一反应是:这就是一个费用流模型?用模拟费用流的方法?
这应该是可以的,但是我忘记了怎么模拟费用流了IOI不可能考模拟费用流。于是我就想了另外一个方法。
首先我们考虑模拟费用流的模型如下图:
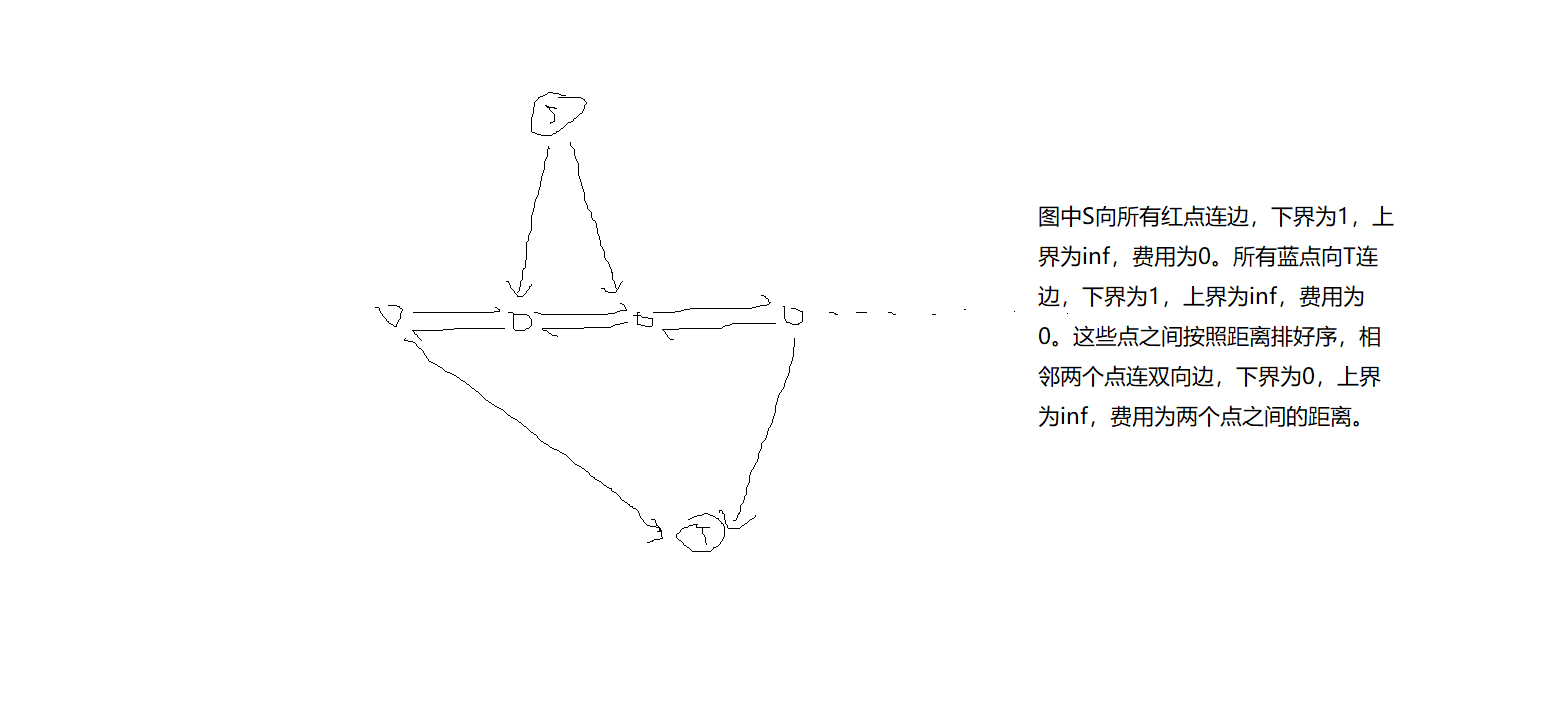
直接费用流复杂度比较大,我们把它换成一个dp。设\(f_{i, j}\)表示考虑了前\(i\)个点,且\(i\)个点后面一条在图中横着的边的流量为\(j\)的时候,最小费用是多少。注意这里从左到右的流量记为正,否则记为负。转移的时候如果第\(i\)个点是红点,就枚举\(S\)向这个点连的边的流量,否则枚举这个点向\(T\)连的边的流量。根据流量平衡方程我们算出前一条横着的边的流量。
用前缀/后缀min将这个算法优化至\(O((r + b)^2)\),可以获得\(7\)分的成绩。
代码如下:
#include "wiring.h"
#include <bits/stdc++.h>
using namespace std;
const int N = 205, M = 205;
const long long inf = 1000000000000000ll;
int n, m;
long long f[N + M][N + M << 2], g[N + M][N + M << 2];
pair<long long, int> vec[N + M];
long long min_total_length(std::vector<int> r, std::vector<int> b) {
n = r.size(), m = b.size();
for (int i = 1; i <= n; i++) vec[i] = make_pair(r[i - 1], 0);
for (int i = 1; i <= m; i++) vec[i + n] = make_pair(b[i - 1], 1);
sort(vec + 1, vec + n + m + 1);
for (int i = 0; i <= (n + m << 2); i++) f[0][i] = inf;
f[0][n + m << 1] = 0ll;
for (int i = 1; i <= n + m; i++) {
for (int j = 0; j <= (n + m << 2); j++) {
f[i][j] = f[i - 1][j];
if (i) {
int tim = j - (n + m << 1);
if (tim < 0) tim = -tim;
f[i][j] += 1ll * (vec[i].first - vec[i - 1].first) * tim;
}
}
if (vec[i].second) {
g[i][0] = f[i][0];
for (int j = 1; j <= (n + m << 2); j++) g[i][j] = min(f[i][j], g[i][j - 1]);
for (int j = 0; j <= (n + m << 2); j++) {
if (!j) f[i][j] = inf;
else f[i][j] = g[i][j - 1];
}
}
else {
g[i][n + m << 2] = f[i][n + m << 2];
for (int j = (n + m << 2) - 1; j >= 0; j--) g[i][j] = min(f[i][j], g[i][j + 1]);
for (int j = 0; j <= (n + m << 2); j++) {
if (j == (n + m << 2)) f[i][j] = inf;
else f[i][j] = g[i][j + 1];
}
}
}
return f[n + m][n + m << 1];
}
注意这里实现的时候用了平移的技巧处理第二维为负数的情况。
接下来我们考虑优化这个dp的方法。
把这个dp状态的第二维看成一个函数,那么我们会发现,需要进行的操作有:函数向左或向右平移一个单位,给它取前缀\(\min\),给它取后缀\(\min\),以及给它加上\(k \lvert x \rvert\)。
容易发现这些操作都不会改变函数下凸的性质。因此我们可以用APIO2016T2,我自己出的名为“穿越”的联测题等题目的方法。用一个set/multiset维护这个函数的每个拐点的位置以及斜率的变化值,再用\(O(1)\)的变量维护最左边/右边的那一段的斜率和截距,再维护偏移量(为了进行平移操作),就可以实现平移操作和加\(k \lvert x \rvert\)操作。而取前缀\(\min\)操作相当于是把一个函数图像的右边递增的一段变为常值函数,如下图所示:

因此我们可以在set/multiset上不断删除右边的拐点,直到右边那一段斜率刚好\(\ge 0\)(也就是再删去一个就\(<0\)了)为止。然后在改变恰好一个拐点的斜率变化量就可以实现前缀\(\min\)操作。同理我们可以实现后缀\(\min\)操作。
注意到这里的复杂度可以被拐点个数的减少量bound住,所以总复杂度仍然为\(O(n \log n)\)。
满分代码如下:
#include "wiring.h"
#include <bits/stdc++.h>
using namespace std;
const int N = 100005, M = 100005;
const long long inf = 1000000000ll;
int n, m;
pair<long long, int> vec[N + M];
multiset<pair<int, long long> > que;
long long min_total_length(std::vector<int> r, std::vector<int> b) {
n = r.size(), m = b.size();
for (int i = 1; i <= n; i++) vec[i] = make_pair(r[i - 1], 0);
for (int i = 1; i <= m; i++) vec[i + n] = make_pair(b[i - 1], 1);
sort(vec + 1, vec + n + m + 1);
int val = 0;
long long k_l = -inf, k_r = inf, val_l = inf * (n + m);
que.insert(make_pair(0, inf << 1));
for (int i = 1; i <= n + m; i++) {
if (i > 1) {
que.insert(make_pair(val, (vec[i].first - vec[i - 1].first) << 1));
k_l -= vec[i].first - vec[i - 1].first, k_r += vec[i].first - vec[i - 1].first;
val_l += (vec[i].first - vec[i - 1].first) * (n + m + val);
}
if (vec[i].second) {
val++;
while (k_l < 0ll) {
pair<int, long long> pi = *que.begin();
if (k_l + pi.second < 0ll) {
val_l -= pi.second * (pi.first + n + m);
k_l += pi.second;
}
else {
val_l += k_l * (pi.first + n + m);
que.insert(make_pair(pi.first, k_l + pi.second));
k_l = 0ll;
}
que.erase(que.find(pi));
}
}
else {
val--;
while (k_r > 0ll) {
pair<int, long long> pi = *que.rbegin();
if (k_r - pi.second > 0ll) k_r -= pi.second;
else {
que.insert(make_pair(pi.first, pi.second - k_r));
k_r = 0ll;
}
que.erase(que.find(pi));
}
}
}
int lst = -n - m;
long long ans = val_l;
for (multiset<pair<int, long long> > :: iterator it = que.begin(); it != que.end(); it++) {
pair<int, long long> pi = *it;
if (pi.first < val) {
ans += k_l * (pi.first - lst);
k_l += pi.second, lst = pi.first;
}
else {
ans += k_l * (val - lst);
lst = val;
break;
}
}
if (lst < val) ans += k_l * (val - lst);
return ans;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号