翻译(2): How to Write a 21st Century Proof

原文：Computer Scientist Tells Mathematicians How To Write Proofs

对比一下下面两个证明哪个更好？

• 版本一：

“A square and 10 roots are equal to 39 units. The question therefore in this type of equation is about as follows: what is the square which combined with ten of its roots will give a sum total of 39? The manner of solving this type of equation is to take one-half of the roots just mentioned. Now the roots in the problem before us are 10. Therefore take 5, which multiplied by itself gives 25, an amount which you add to 39 giving 64. Having taken then the square root of this which is 8, subtract from it half the roots, 5 leaving 3. The number three therefore represents one root of this square, which itself, of course is 9. Nine therefore gives the square.”

• 版本二：

\(x^2+10x=39. Find x^2.\)
\(x^2+10x+52=39+52\)
\((x+5)2=64\)
\(x+5=8\)
\(x=3\)
\(x^2=9\)

Leslie Lamport (https://en.wikipedia.org/wiki/Leslie_Lamport) 又在教数学家们如何写证明了。他说在一个小范围调查显示，1/3的出版物（包括经过同行评议, peer reviewed）包含一个错误的定理，有一些是由于证明本身是错的，有些是由于引用了有错的定理。这篇文章认为，17世纪大家都是用文字来写数学证明，冗长又容易出错，如今很难想象没有代数符号的话数学证明将会多么复杂，因此作者认为虽然Lamport的方式不是那么容易接受，但是也许是对的，正如上面的例子，在代数符号被普遍接受之前，同样的证明很长又不易被人们所掌控，而有了代数系统，就简洁明了。

注：符号提供了组合抽象的工具，我认为很多概念，由于缺乏有效的可组合抽象工具，导致人们需要用线性的文字去长篇描述，并且还达不到清晰解释的目的。也因此，在没有共识的通用可组合抽象符号系统的领域，如何把思想、概念用线性文字描述清楚，就成为了人们的一项重要技能，一般来说写作者经过长时间的写作训练，可以达到更好的组织效果。但是，从这个角度来看，说明这个方面还不能成长为一门使用上符号系统的学科，想必这可以作为“文科”与“理科”之间的边界。

Lamport在《How to Write a 21st Century Proof》这篇2011年的文章里提出了他认为更好的编写数学证明的方式：
https://www.microsoft.com/en-us/research/uploads/prod/2016/12/How-to-Write-a-21st-Century-Proof.pdf

首先，Lamport认为文字形式的证明，很难看清楚一句话的作用：

• 是否包含一个新的断言（assert）
  • 如果是，那么文本中描述的事实（fact）是否可以明显看出结论是对的还是错的。
• 是否使用了上一句话的断言、状态(state)、和事实。

Lamport提出了清晰证明的两个核心要素：

• 命名（name），对所有的事实（fact）命名，让人一眼看出哪个事实被使用了。
• 结构化（structure），证明中补充文本(prose，有更好的翻译么)让读者理解此刻正在说明的要点，但是让人难以掌控整个完整的证明逻辑。结构化则可以让这个过程清晰可见。结构化也使得错误消除更容易。

注：对这点，我深表赞同，即使只是纯文本方面，适当使用结构化，可以使得重要的逻辑清晰可见。写作课上，写作老师一般也推荐多多使用：list、table、picture，这都是为了突破线性文本（可以看作是array）的局限，在线性文本中，制造结构效果。例如，2-3层的短list就是一个适合经常使用的结构。

Lamport认为自己早期犯的一个错误是提倡证明同时满足下面两点：

• 使得读者易于理解
• 更加严密

但是同时做到这两个目标对数学家来说是一个有门槛的事情。Lamport试着把这两个目标分开，通过结构化证明，使得数学家们更容易看到自己的证明是否草率。重要的是要停止17世纪的证明写法。

第二个错误是早期Lamport认为自己懂得最好的证明写法。Lamport基于自己过去20多年写证明的经验，提出结构化的证明写法，并鼓励数学家们发现可以改进的地方，就可以对这种方式做改进。大家不必再像17世纪那样写证明了。

文章中也介绍形式证明，因为作者认为通过形式证明的训练，数学家们可以更好地写通常的证明，从而达到目的。

通过一个例子做对比：

版本一，现在的数学证明常见写法：

版本二，使用structure+fact：

通过结构化，读者直观地看到了证明中的5个关键步骤以及每个步骤的断言（assert）是如何被前面已经证明过的事实（fact）所证明。并且，通过结构化证明，可以看到第1步并不是显而易见的，第1步需要读者自己做推导（数学证明里到处都是这类“显而易见”，但是需要读者自己发现并get到“此处隐含着一个点，你自己推导一下”。Lamport认为至少可以通过在第5个步骤的地方展开并显式的表达这个洞：

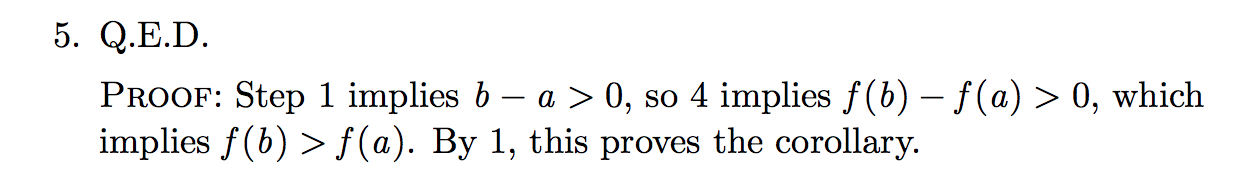
但是这还不够，在结构化证明里，可以进一步改进步骤1和步骤5，结果如下：

最后的证明步骤比原来的方式有了巨大的提升。

注：这个过程，对于程序员来说是很好理解的，结构化编程就是这种思想的典型体现。以及，在给程序编写注释的时候，结构化的注释也往往更清晰。例如：

你会问说，细化到怎样的粒度才可以？比如1.1和1.2是否还需要细化？这取决于你的读者，如果是针对初学者，则需要以初学者的视角来写。如果是给你自己的，那么，只要你觉得一个地方有一点点可能不正确，你就应该细化它。避免错误的做法，就是你应该对你的所有定理都100%确认它是对的，你应该无情的怀疑可能发生的错误。

注：在程序的代码中，这一点也是类似的，你应当无情地对绝对不应该发生的条件做断言。这个注释也说明了目前数学和程序的区别之一是，程序是可以执行的，同样的断言，在程序里面会直接造成崩溃，而数学证明里的断言，目前还是靠人来做peer-review。除非，你选择使用形式证明的方式去断言。

观察步骤2，它依然是文本形式的证明，每一点都需要补充细节才能知道是否是正确的。传统的数学证明方式，将会引入一堆的引理，引理多起来就把你淹没在细节之中，你看不到证明的完整轮廓。看看结构化证明的方式：

未来的阅读会越来越多地使用超文本（Hypertext）的方式展示数学证明，随着VR等现代技术的进步，也许还会有更新的方式展示。使用超文本的方式展示结构化的证明，证明甚至可以展开到那些基本的公理。则读者可以根据自己的需要展开到足够的层级去阅读，以确保自己100%理解和验证了证明的正确性。

接下来的一节，Lamport简单介绍了形式验证系统TLA+的内容，这部分就跳过了，可以在TLA+的网站上（ http://lamport.azurewebsites.net/tla/tla.html ）进一步学习，按Lamport的说法，现在的数学虽然还不能直接达到用这种严格的形式验证系统证明，但是接受形式验证系统的训练，则可以训练数学家们更好的写无错的结构化证明。

最后，Lamport自己是一个计算机科学家，但是接受的是数学教育，在并发算法的研究中，发现了结构化证明的方式。在并发算法里面，一个集合是否非空，都会导致算法里有无数的BUG，证明算法的正确性十分复杂和琐碎，使用传统的数学证明方式，Lamport发现自己很难确认是否忘记了一个某个细节的验证。计算机科学家掌控复杂性的方式之一就是层次结构，这使得层次结构证明是一个自然的对传统数学证明方式的升级。作者从1991年发表并发算法的论文开始，大部分论文都是以结构化的方式证明。Lamport用这种方式重新发现了一个Schröder–Bernstein定理的证明错误。有一个数学家发邮件给Lamport说他用结构化证明的方式发现不了自己论文里的错误，Lamport让他把证明发过来，结果这个数学家回邮件说他发现他在把手写的证明打下来（电子化）的过程中发现里错误！可见消灭错误需要十分小心。

作为对比，Lamport这些年的论文都是这么写的，读者们很少问他写法的问题，结构化的写法清晰，使得读者直接关注证明的内容，而不会在形式上有疑问。这进一步说明了大量采用这种证明写法是可行的。把在线论文的结构化形式证明作为Appendix，期刊的编辑找审稿人阅读，收到正面的反馈：

I have found the hierarchical structuring of proofs to be very helpful, if read top-down according to the suggestions of the authors. In fact, it might well be the only way to present long proofs. . . in a way that is both detailed (to ensure correctness) and readable. For long proofs, I think that describing the idea of the proof in a few words at the beginning (if appropriate) would help make them more understandable. . . . But in general, I found the structured approach very effective.

针对结构化证明，其他数学家们提出的典型问题（FAQ）：

• 结构化证明是否太复杂了，Lamport的证明PPT常常要翻好几页？Lamport回答说，看上去简短的证明，实际上漏洞百出，而结构化证明则能消灭错误。证明之所以为证明，是要消除错误的。

• 结构化证明没有解释为什么这样证明？Lamport回答说，证明的结构和为什么能证明是两件事，能任意添加结构的证明方式更有能力（表达力）解释为什么证明能工作。

• 结构化证明不是伟大的文学？Lamport回答说，证明不是文学，证明是数学，证明应该首先为清晰无错服务，而不是文学。

最后，Lamport再次无情的做了对比：

版本一，“文学的方式”：

The number e raised to the power of i times π, when added to 1, equals 0

版本二，数学的方式：

Lamport说，数学家们应该用21世纪的方式写证明。

--end--