[容斥][数论]JZOJ 5810 简单的玄学
分析
对于题目所要求的方案,我们比较难求,可以容斥转换为全部都不选的概率
而这个概率为: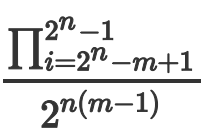 ,分母可以简单求出,但是分子有问题。
,分母可以简单求出,但是分子有问题。
但是很快发现,当m>10^6+3时,分子中必有一个等于模数的因子,即为0
然后约分,分母是2的幂,所以我们求出乘积中的2的次数即可
然后对于0≤a<2n,2n的次数和2n-a的次数相同,所以求出(m-1)!的所有2的次数即可
求m!的2的次数有O(log2(m))的做法,在此不作过多叙述
然后搞一波逆元就行

#include <iostream> #include <cstdio> #include <cmath> using namespace std; typedef long long ll; const ll P=1e6+3; ll n,m; ll Power(ll x,ll y) { ll ans=1; while (y) { if (y&1) ans=ans*x%P; x=x*x%P; y>>=1; } return ans; } int main() { freopen("random.in","r",stdin); freopen("random.out","w",stdout); scanf("%lld%lld",&n,&m); if ((double)log(m)/log(2)>n) { printf("1 1"); return 0; } ll fz,fm=Power(Power(2ll,n),m-1ll); ll yf=0; for (ll i=2ll;i<m;i<<=1ll) yf+=(m-1)/i; fm=fm*Power(Power(2ll,yf),P-2ll)%P; if (m<=P) { ll p=Power(2,n);fz=1; // for (ll i=0;i<m;i++) fz=fz*(p+i)%P; for (ll i=p-m+1;i<p;i++) fz=fz*i%P; fz=fz*Power(Power(2ll,yf),P-2ll)%P; } else fz=0; printf("%lld %lld",((fm-fz)%P+P)%P,fm); fclose(stdin);fclose(stdout); }
在日渐沉没的世界里,我发现了你。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号