数据结构 二叉树

1-1

某二叉树的后序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无右孩子。

正确：

后序遍历：左右根；

中序遍历：左根右；

（左）（根）（右） ==（左）（右）（根）

（右） = NULL --------> (左）（根）==（左）（根）

得：二叉树任何节点一定都没右子节点；

1-2

某二叉树的后序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无左孩子

错误：

后序遍历：左右根；

中序遍历：左根右；

令 （左）=NULL

后续遍历 （右）（根）

中序遍历 （根）（右）

顺序相反，不满足遍历序列相同的题目的前提

得：二叉树中任何结点一定都无左孩子结论错误

 

1-3  存在一棵总共有2016个结点的二叉树，其中有16个结点只有一个孩子。

错误：

没确定是什么类型的二叉树；

二叉树的类型：

满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。 

完全二叉树：一棵二叉树至多只有最下面的一层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，则此二叉树成为完全二叉树

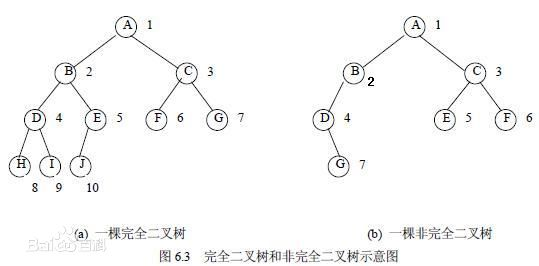
平衡二叉树：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树 

1-4 

若A和B都是一棵二叉树的叶子结点，则存在这样的二叉树，其前序遍历序列为...A...B...，而中序遍历序列为...B...A...。 

错误：

遍历顺序：

中序遍历 ：左根右
后序遍历 ：左右根
前序遍历 ：根左右

确定了A，B都不是根节点；
根据三种遍历顺序，确认都是 左右 顺序的遍历
前序遍历确认了 A 先于 B 被遍历， 那么中序遍历也必须是 A 先于 B ；

 

1-5：

若一个结点是某二叉树的中序遍历序列的最后一个结点，则它必是该树的前序遍历序列中的最后一个结点。 

 错误：

特例： A-B-C 一条线上，C是根节点；

中序遍历：ABC

前序遍历：CBA

 

 1-6

某二叉树的前序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无左孩子

正确：

中序遍历 ：左根右
后序遍历 ：左右根
前序遍历 ：根左右令（左）=NULL
中序：（根）（右）==前序：（根）（右）

 

1-7

已知一棵二叉树的先序遍历结果是ABC,　则CAB不可能是中序遍历结果。

正确：

遍历比较多，强试就行：

1.找出根节点：A

2.可能的树的类型，本题目只有两种

3.这两种树的中序遍历都不是CAB，一个是BAC，一个是CBA

 

 

节选选择题

2-2

如果一棵非空k（k≥2 叉树T中每个非叶子结点都有k个孩子，则称T为正则k叉树。若T的高度为h（单结点的树h=1），则T的结点数最少为：

 

 

 

---

 

这不就是满树(h0 = h-1) 节点数 + 1吗

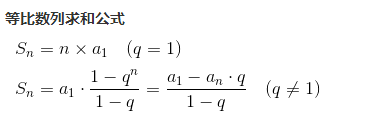
这道题目是 k⁰ +k¹ +k²+.....k^h-2   共有 h-1 个元素

1*（k^h-1-1）/(k-1) + 1，选A？

NONONO，读题可知：

最少的情况是根节点加上根节点的k个孩子，加上根节点的第一个孩子的k个孩子，再加上''''''，以此类推；

1+k+k+k+k+k （加 h-1 个） ，答案就是(h-1)*k+1，嗯，没有，选D；

 

---

2-3

要使一棵非空二叉树的先序序列与中序序列相同，其所有非叶结点须满足的条件是：

---

中序遍历 ：左根右
后序遍历 ：左右根
前序遍历 ：根左右

 令（根左右）==（左根右）；

令 左 =NULL，即为 （根右）==（根右），成立，成立条件是没有左子树，也就是只有右子树。

---

 

2-4

已知一棵二叉树的树形如下图所示，其后序序列为{ e, a, c, b, d, g, f }。树中与结点a同层的结点是：

 

---

 

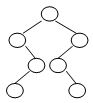
后序遍历：左右根

二叉树递归遍历代码

这是前序列遍历，其余的根据顺序略微改动下位置就好、

void preorder(bintree t){
    if(t){
        printf("%c ",t->data);
        preorder(t->lchild);
        preorder(t->rchild);
    }
}

　　

第一层： f

第二层： c g

第三层： a d

第四层： e b

 

---

 

 

---

 

题目可知：根节点是 4

后序遍历序列是{ 1, 3, 2, 6, 5, 7, 4 }

中序遍历序列是{ 1, 2, 3, 4, 5, 6, 7 }

对照进行划线；可知根节点左子树有 3 节点，右子树也是3节点，根据理解进行构图

对于左子树来说，根节点是 2 ，对右子树来说，根节点是 7，这是根据后序遍历确定的；

三个元素，确定了根节点，很容易的得到左子树为：

 

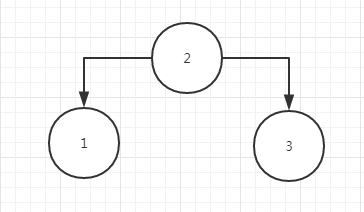
三个元素，确定了根节点7，也可得到右子树为：

中序遍历是： 5 6 7 。可以确定，7 节点没有右子树，根据后序遍历可得右子树：

 

综上所诉：树为

然后就看图回答问题；

 

完全二叉树的定义：

子节点只有一个的节点数目只有 0 或 1 个！（简化版定义），建议去看正规的介绍；

二叉搜索树的定义：

左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值

即：对任何一个节点T来说：  T->Left->data  <  T->data   <   T->right->data;

 

---

 

2-11

任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序

 

遍历顺序 ，令所有遍历中的 根==NULL 遍历顺序都是 左右，即左节点先于右节点，不会改变顺序；

 

 2-xx

先序序列遍历为 a b c d 的二叉树有多少个？

14

运用卡特兰算式 ， n = 4 ，ans = C（n,2*n）/(n+1） = 14

 

---

2-16

某二叉树的前序和后序遍历序列正好相反，则该二叉树一定是；

前序：NLR

后序：LRN

正好相反，只能让R==NULL||L==NULL

应该是二叉树的每个结点都只有一个（左或右）子树时，先序和和后序正好相反

这道题目我对答案暂时保持怀疑：

---

 

 

对于函数与编程题目可能会出现的考点，进行了一个汇总：

1.二叉树的一些操作

 

2.由二叉树的前序遍历(后序遍历)和中序遍历输出后序遍历(前序遍历)

 

---

 

 

 

求个关注或推荐！