机器学习--决策树算法(ID3 C4.5)

在生活中，“树”这一模型有很广泛的应用，事实证明，它在机器学习分类和回归领域也有着深刻而广泛的影响。在决策分析中，决策树可以明确直观的展现出决策结果和决策过程。如名所示，它使用树状决策模型。它不仅仅是在数据挖掘中用户获取特定目标解的策略，同时也被广泛的应用于机器学习。

如何使用树来表示算法

为此，我们考虑使用泰坦尼克号数据集的示例，以预测乘客是否会生存。下面的模型使用数据集中的3个特征/属性/列，即性别，年龄和SIBSP（配偶或儿童的数量）。这是一棵体现了人性光辉的决策树。

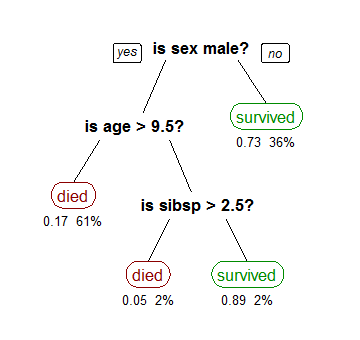
树的形状是一棵上下颠倒的决策树，叶子节点在下，根节点在上。在图像中，黑色中的粗体文本表示条件/内部节点，基于树分成分支/边缘。不再分裂的分支结束是决策/叶子，在这种情况下，乘客是否被死亡或幸存，分别表示为红色和绿色文本。

虽然，一个真实的数据集将有很多功能，这只是一个更大的树中的部分分支，但你不能忽略这种算法的简单性。该特征重要性是明确的，可以轻易查看决策关系。该方法更常见于来自数据的学习决策树，并且在树上被称为分类树，因为目标是将乘客分类为幸存或死亡，上面所展示的决策树就是分类树。回归树以相同的方式表示，例如用于预测房子价格的连续价值。通常，决策树算法被称为CART或分类和回归树。

那么，算法生成的背后发生了什么呢？如何生成一个决策树取决于选择什么特征和在何种情况下进行分裂，以及在什么时候停止。因为一棵树通常是随意生长的，你需要修剪它，让它看起来漂亮（研究如何生成决策树）。

ID3算法

ID3算法生成决策树

ID3算法（Iterative Dichotomiser 3）是决策树生成算法的一种，基于奥卡姆剃刀原理(简约原则) \(^{1}\)。是Ross Quinlan发明的一种决策树算法，这个算法的基础就是上面提到的奥卡姆剃刀原理，越是小型的决策树越优于大的决策树，尽管如此，也不总是生成最小的树型结构，而是一个启发式算法。在信息论中，期望信息越小，那么信息增益\(^{2}\)就越大，从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂（决策树分支）。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。

假设你是水果商人，现在有一个客人来你的摊位购买西瓜，请你使用ID3构建一个决策树，帮助客人挑选一个好瓜。

凭借你的经验，你总结出了如下判断规律。

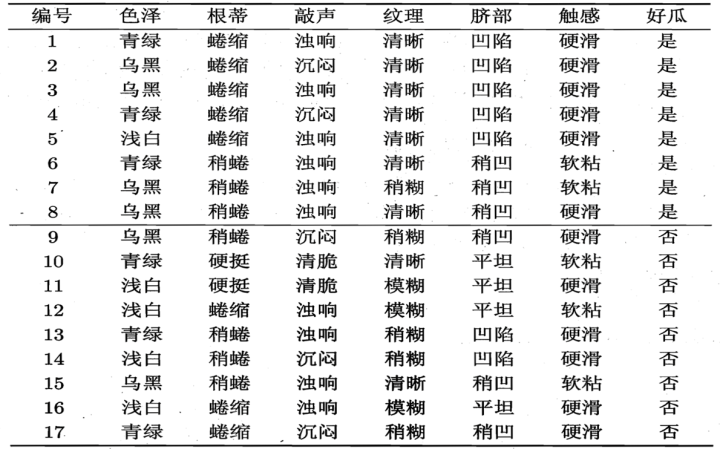
好瓜占 \(\frac{8}{17}\)，坏瓜占 \(\frac{9}{17}\) ，根节点的信息熵为：

\[H(X) = - \sum_{i=1}^{2}{p_i\log{p_i}} = -(\frac{8}{17}\log{\frac{8}{17}}+\frac{9}{17}\log{\frac{9}{17}}) = 0.998 \]

色泽有 $3 $ 个可能的取值 $ { 青绿，乌黑，浅白}$

\(X_1(色泽=青绿) = \{1, 4, 6, 10, 13, 17\}\)，正例 \(\frac{3}{6}\)，反例 \(\frac{3}{6}\)

\(X_2(色泽=乌黑) = \{2, 3, 7, 8, 9, 15\}\)，正例 \(\frac{4}{6}\)，反例 \(\frac{2}{6}\)

\(X_3(色泽=浅白) = \{5, 11, 12, 14, 16\}\)，正例 \(\frac{1}{5}\)，反例 \(\frac{4}{5}\)

$3 $ 个分支节点的信息熵为

\[H(X_1) = -(\frac{1}{2}\log{\frac{1}{2}}+\frac{1}{2}\log{\frac{1}{2}}) = 1.000 \\ H(X_2) = -(\frac{1}{3}\log{\frac{1}{3}}+\frac{2}{3}\log{\frac{2}{3}}) = 0.918 \\ H(X_3) = -(\frac{1}{5}\log{\frac{1}{5}}+\frac{4}{5}\log{\frac{4}{5}}) = 0.722 \]

计算信息增益

\[I(X，色泽) = H(X) - H(X|色泽) = 0.998 - \sum_{i=1}^{3} H(X|X_i) \\ = 0.998 - (\frac{6}{17}\times 1.000 + \frac{6}{17}\times 0.918 + \frac{5}{17}\times 0.722) = 0.109 \]

同理，我们可以求出其他属性的信息增益

\[I(X,根蒂) = 0.143 \\ I(X,敲声) = 0.141 \\ I(X,纹理) = 0.381 \\ I(X,脐部) = 0.289 \\ I(X,触感) = 0.006 \]

选择其信息增益 \(I\) 最大的属性进行分支

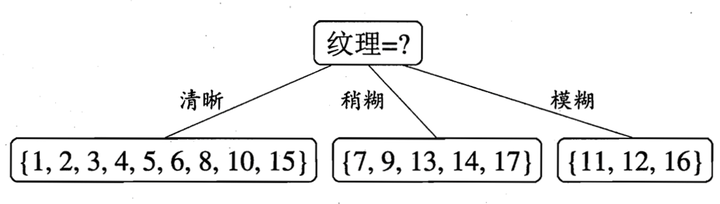
于是，我们可以得到了三个子结点，对于这三个子节点，我们可以递归的使用刚刚找信息增益最大的方法进行选择特征属性，比如：\(X_1(纹理=清晰) = \{1, 2, 3, 4, 5, 6, 8, 10, 15\}\)，第一个分支结点可用属性集合\(\{色泽、根蒂、敲声、脐部、触感\}\)，基于 \(X_1\) 各属性的信息增益，分别求的如下：

\[I(X_1,色泽) = 0.043 \\ I(X_1,根蒂) = 0.458 \\ I(X_1,敲声) = 0.331 \\ I(X_1,脐部) = 0.458 \\ I(X_1,触感) = 0.458 \]

于是我们可以选择特征属性为\(根蒂，脐部，触感\)三个特征属性中任选一个（因为他们三个相等并最大），其它俩个子结点同理，然后得到新一层的结点，再递归的由信息增益进行构建树即可
最终的决策树如下：

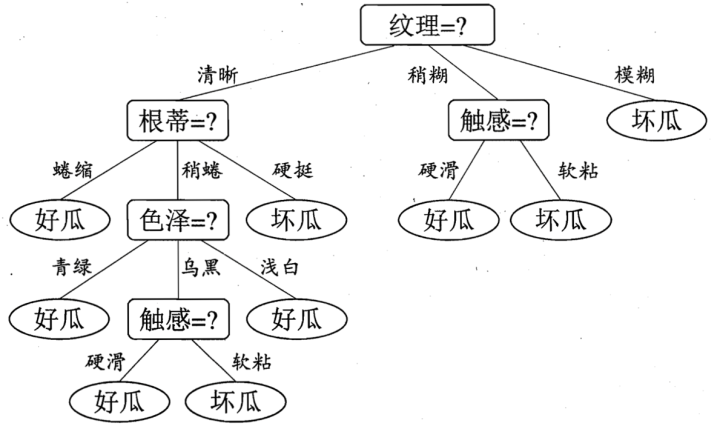
ID3算法虽然提出了新思路，但是还是有很多值得改进的地方。　　

• ID3没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。这大大限制了ID3的用途。
• ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。如果校正这个问题呢？
• ID3算法对于缺失值的情况没有做考虑
• 没有考虑过拟合的问题

C4.5算法

使用 C4.5算法生成决策树

Ross Quinlan在C4.5算法中改进了上述4个问题。

• 对于第一个问题，不能处理连续特征， C4.5的思路是将连续的特征离散化。比如 \(m\) 个样本的连续特征 \(A\) 有 \(m\) 个，从小到大排列为 \(a_1,a_2,...,a_m\) ,则C4.5取相邻两样本值的平均数，一共取得 \(m-1\) 个划分点，其中第 \(i\) 个划分点 \(T_i\) 表示为：\(T_i = \frac{a_i+a_{i+1}}{2}\) 。对于这 \(m-1\) 个点，分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为 \(a_t\),则小于 \(a_t\) 的值为类别 \(1\)，大于 \(a_t\) 的值为类别 \(2\)，这样我们就做到了连续特征的离散化。要注意的是，与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。

• 第二个问题，信息增益作为标准容易偏向于取值较多的特征的问题。我们引入一个信息增益比\(^{6}\)的变量，它是信息增益和特征熵的比值。特征数越多的特征对应的特征熵越大，可以校正信息增益容易偏向于取值较多的特征的问题。

• 对于第三个缺失值处理的问题，主要需要解决的是两个问题，一是在样本某些特征缺失的情况下选择划分的属性，二是选定了划分属性，对于在该属性上缺失特征的样本的处理。

  对于第一个子问题，对于某一个有缺失特征值的特征 \(A\)。C4.5的思路是将数据分成两部分，对每个样本设置一个权重（初始可以都为1），然后划分数据，一部分是有特征值 \(A\) 的数据 \(D_1\)，另一部分是没有特征 \(A\) 的数据 \(D_2\). 然后对于没有缺失特征 \(A\) 的数据集 \(D_1\) 来和对应的 \(A\) 特征的各个特征值一起计算加权重后的信息增益比，最后乘上一个系数，这个系数是无特征 \(A\) 缺失的样本加权后所占加权总样本的比例。

  对于第二个子问题，可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征 \(A\) 的样本 \(a\) 之前权重为 \(1\)，特征 \(A\) 有 \(3\) 个特征值 \(A_1,A_2,A_3\)。 \(3\) 个特征值对应的无缺失 \(A\) 特征的样本个数为 \(2,3,4\).则\(a\) 同时划分入 \(A_1，A_2，A_3\)。对应权重调节为 \(2/9,3/9, 4/9\)。

• 对于第4个问题，C4.5引入了正则化系数进行初步的剪枝

客人对你挑选的西瓜很满意，这次要一次性购买多个西瓜，请你再用C4.5算法构建一个决策树帮助客人挑选西瓜

根据上面的ID3算法，我们已经求出了部分信息增益信息

\[I(X,根蒂) = 0.143 \\ I(X,敲声) = 0.141 \\ I(X,纹理) = 0.381 \\ I(X,脐部) = 0.289 \\ I(X,触感) = 0.006 \\ I(X,色泽) = 0.109 \]

然后计算特征熵(以色泽为例)

\[H_{色泽}(X) = - \frac{6}{17}\log{\frac{6}{17}} - \frac{6}{17}\log{\frac{6}{17}} - \frac{5}{17}\log{\frac{5}{17}} = 1.579 \]

根据特征熵计算信息增益比

\[I_R(X,色泽) = \frac{I(X,色泽)}{H_{色泽}(X)} = \frac{0.109}{1.579} = 0.069 \]

同理可以计算出其他信息增益比，以信息增益比 $ I_R$替代ID3算法的信息增益 \(I\) 作为分支依据，选择信息增益比最大的属性进行构建分支。

---

[1] 奥卡姆剃刀 : 其含义是：在其他条件一样的情况下，选择简单的那个。

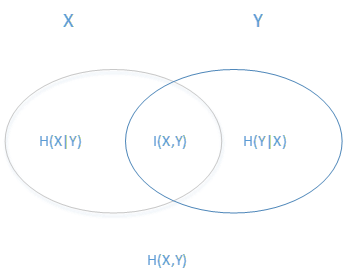
[2] 信息增益 : 信息增益 = 熵 \(^{3}\)- 条件熵\(^{4}\)。表示在一个条件下，信息不确定性减少的程度，即下图 $ I(X,Y) = H(X) - H(X|Y)$。

[3] 熵 : 熵这个概念最早起源于物理学，在物理学中是用来度量一个热力学系统的无序程度，而在信息学里面，熵是对不确定性的度量。在1948年，香农引入了信息熵，将其定义为离散随机事件出现的概率，一个系统越 是有序，信息熵就越低，反之一个系统越是混乱，它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。具体的，随机变量 \(X\) 的熵的表达式如下：

\[H(X) = - \sum_{i=1}^{n}{p_i\log{p_i}} \]

其中 \(n\) 代表 \(X\) 的 \(n\) 种不同的离散取值，而 \(p_i\) 代表 \(X\) 取值为 \(i\) 的概率，\(log\) 是以 \(2\) 或 \(e\) 为底的对数。

举个例子，比如 \(X\) 有 \(2\) 个可能的取值，而这两个取值各为 \(\frac{1}{2}\) 时 \(X\) 的熵最大，此时 \(X\) 具有最大的不确定性。熵为 :

\[H(X) = -(\frac{1}{2}\log{\frac{1}{2}} + \frac{1}{2}\log\frac{1}{2}) = \log{2} \]

如果一个值概率大于 \(\frac{1}{2}\) ，另一个值概率小于 \(\frac{1}{2}\) ，则不确定会减少。比如一个概率 $ \frac{1}{3}$ ，另一个概率 $ \frac{2}{3}$ ，则对应熵为:

\[H(X) = -(\frac{1}{3}\log{\frac{1}{3}} + \frac{2}{3}\log\frac{2}{3}) = \log{3} - \frac{2}{3}\log{2} < \log{2} \]

[4] 条件熵 ：熟悉了一个变量的熵，很容易推导出多个变量的联合熵，这里给出两个变量 $ X , Y$ 的联合熵表达式 :

\[H(X,Y) = -\sum_{x_i\in{X}}\sum_{y_i\in{Y}} p(x_i,y_i)\log{p(x_i,y_i)} \]

有了联合熵，又可以得到条件熵的表达式 \(H(X|Y)\)，\(𝐻(X|Y)\) 定义为在给定条件 \(𝑌\) 下，\(X\) 的条件概率分布的熵对 \(Y\) 的数学期望[5]。条件熵类似于条件概率,它度量了我们的 \(X\) 在知道 \(Y\) 以后剩下的不确定性。表达式如下:

\[H(X|Y) = -\sum_{x_i\in{X}}\sum_{y_i\in{Y}} p(x_i,y_i)\log{p(x_i|y_i)} = \sum_{j=1}^{n}H(X|y_j) \]

\[\begin{cases} H(X|Y) = H(X) - I(X,Y)\\\ \\\ H(X,Y) = H(X) + H(Y) - I(X,Y) \end{cases} \\\ 推导得: H(X|Y) = H(X,Y) - H(Y) \]

[5] 数学期望 ：试验中每次可能的结果乘以其结果概率的总和。

[6] 信息增益比 : 设信息增益比 $ I_R(D,A)$，它是信息增益和特征熵的比值。表达式如下：

\[I_R(D,A) = \frac{I(D,A)}{H_A(D)} \]

如果要用上述习惯的方式表述就是 设信息增益比为 \(I_R(X,Y)\)

\[I_R(X,Y) = \frac{I(X,Y)}{H_A(X)} = \frac{H(X) - H(X|Y)}{H_A(X)} \]

其中 \(D (或X)\)为样本特征输出的集合，\(A(或Y)\)为样本特征，对于特征熵\(H_A(D)\), 表达式如下:

\[H_A(D) = -\sum_{i=1}^{n}\frac{|D_i|}{|D|}log_2\frac{|D_i|}{|D|} \]

其中 \(n\) 为特征 \(A\) 的类别数， \(D_i\) 为特征 \(A\) 的第 \(i\) 个取值对应的样本个数。\(|D|\) 为样本个数。

参考资料

[1] Prashant Gupta. Decision Trees in Machine Learning [EB/OL]

[2] scikit-learn 中文社区,决策树 [EB/OL]

[3] 维基百科 ID3 算法 [EB/OL]

[4] 苗煜飞,张霄宏.决策树C4.5算法的优化与应用[J].计算机工程与应用,2015,51(13):255-258+270.

[5] 刘建平.决策树算法原理(上) [EB/OL] 博客园

[6] 行者.决策树--ID3 算法（一）[EB/OL] 博客园

[7] 忆臻.深入浅出理解决策树算法（二）-ID3算法与C4.5算法 [EB/OL] 知乎

[8] AI研究僧.【机器学习（三）】机器学习中：信息熵，信息增益，信息增益比，原理，案例，代码实现 [EB/OL] CSDN