数据结构与算法

数据结构是以某种形式将数据组织在一起的集合，它不仅存储数据，还支持访问和处理数据的操作。

数据的逻辑结构

1.线性结构：数据元素之间存在一个对一个的关系。

2.树形结构：结构中的数据元素存在一个对多个的关系。

3.图形结构或网状结构：结构中的数据元素存在多个对多个的关系。

4.集合结构：结构中的数据元素之间除了同属于一个集合关系外，无其他数据关系。

 

数据类型，是一个值的集合和定义在此集合上的一组操作的总称。

抽象数据类型，是指一个数学模型以及定义在此数据模型上的一组操作。

 

算法是为求解一个问题需要遵循的、被清楚指定的简单指令的集合。

一个算法必须满足五个重要特性：有穷性、确定性、可行性、有输入、有输出。

设计算法要求：正确性、可读性、健壮性、效率与低存储量需求

 

时间复杂度与大O记法

“大O记法”：对于单调的整数函数f，如果存在一个整数函数g和实常数c>0，使得对于充分大的n总有f(n)<=c*g(n)，就说函数g是f的一个渐近函数（忽略常数），记为f(n)=O(g(n))。也就是说，在趋向无穷的极限意义下，函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。

时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的渐近时间复杂度，简称时间复杂度，记为T(n)

时间复杂度的几条基本计算规则

1. 基本操作，即只有常数项，认为其时间复杂度为O(1)
2. 顺序结构，时间复杂度按加法进行计算
3. 循环结构，时间复杂度按乘法进行计算
4. 分支结构，时间复杂度取最大值
5. 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
6. 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

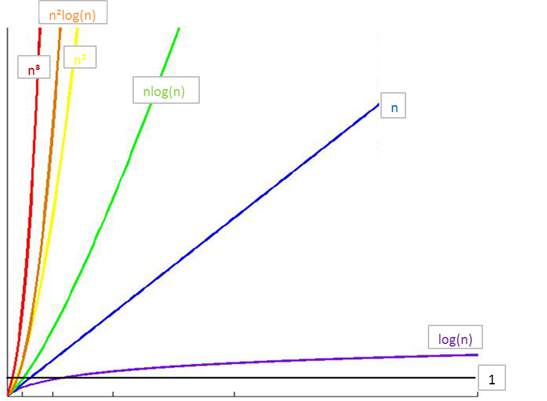
常见时间复杂度之间的关系

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) <O(n²logn) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

 Python list操作

python dict操作

 

python中的list与tuple两种类型采用的顺序表实现技术。list就是采用分离式技术实现的动态顺序表，若将数据区更换为更大的存储空间,则可以不在改变表对象的前提下对其数据区进行扩充,所有使用这个表的地方都不必修改 只要在程序的运行环境(计算机系统)还有空间存储,这种表结构就不会因为满了而导致操作无法进行 这种技术实现的顺序表称为动态顺序表

 在Python的官方实现中，list实现采用了如下的策略：在建立空表（或者很小的表）时，系统分配一块能容纳8个元素的存储区；在执行插入操作（insert或append）时，如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大（目前的阀值为50000），则改变策略，采用加一倍的方法。引入这种改变策略的方式，是为了避免出现过多空闲的存储位置。

 链表(linked list)是由一组被称为结点的数据元素组成的数据结构，每个结点都包含结点本身的信息和指向下一个结点的地址。由于每个结点都包含了可以链接起来的地址信息，所以用一个变量就能够访问整个结点序列。也就是说，结点包含两部分信息：一部分用于存储数据元素的值，称为信息域；另一部分用于存储下一个数据元素地址的指针，称为指针域。链表中的第一个结点的地址存储在一个单独的结点中，称为头结点或首结点。链表中的最后一个结点没有后继元素，其指针域为空。

 

单链表的实现

class Node(object):
    """节点"""
    def __init__(self,elem):
        self.elem =elem
        self.next = None


class SingleLinkList(object):
    """单链表"""

    def __init__(self,node=None):
        self._head = node

    def is_empty(self):
        """判断是否为空"""
        return self._head == None

    def length(self):
        """长度"""
        cur = self._head
        count = 1
        while cur != None:
            count += 1
            cur = cur.next
        return count

    def travel(self):
        """遍历链表"""
        cur = self._head
        while cur != None:
            print(cur.elem,end=',')
            cur = cur.next
        print()

    def add(self,item):
        """头部添加"""
        node =Node(item)
        node.next = self._head
        self._head = Node

    def append(self,item):
        """尾部添加"""
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head
            while cur.next != None:
                cur = cur.next
            cur.next = node

    def insert(self,pos,item):
        """指定位置添加"""
        if pos <= 0:
            self.add(item)
        elif pos > self.length()-1:
            self.append(item)
        else:
            pre = self._head
            count = 0
            while  count < (pos-1):
                count+=1
                pre = pre.next
            node = Node(item)
            node.next = pre.next
            pre.next = node

    def remove(self,item):
        """删除元素"""
        cur = self._head
        pre = None
        while cur != None:
            if cur.elem == item:
                if cur == self._head:
                    self._head = cur.next

                else:
                    pre.next = cur.next
                break

            else:
                pre = cur
                cur = cur.next

    def search(self,item):
        """判断元素是否在链表中"""
        cur = self._head
        while cur != None:
            if cur.elem == item:
                return True
            else:
                cur = cur.next
        return False

if __name__=="__main__":

    li = SingleLinkList()
    print(li.is_empty())
    print(li.length())
    li.append(1)
    print(li.is_empty())
    print(li.length())
    li.append(2)
    li.append(3)
    li.insert(2,100)
    li.travel()
    li.append(9)
    li.remove(2)
    li.travel()
    print(li.search(100))


结果：
True
1
False
2
1,2,100,3,
1,100,3,9,
True

 

操作	链表	顺序表
访问元素	O(n)	O(1)
在头部插入/删除	O(1)	O(n)
在尾部安插入/删除	O(n)	O(1)
在中间插入/删除	O(n)	O(n)

 

 

 

 

 

单向循环链表：单链表的一个变形是单向循环链表，链表中最后一个节点的next域不再为None，而是指向链表的头结点。

class Node:
    """节点"""
    def __init__(self, item):
        self.item = item
        self.next = None

    def __str__(self):
        return str(self.item)


class SinCycLinkedList:
    """单向循环链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        if self.is_empty():
            return 0
        count = 1
        cur = self._head
        while cur.next != self._head:
            # print("cur", cur.item)
            count += 1
            cur = cur.next
        return count

    def travel(self):
        """遍历"""
        if self.is_empty():
            return

        cur = self._head
        print(cur.item)
        while cur.next != self._head:
            cur = cur.next
            print(cur.item)

    def add(self, item):
        """在头部添加一个节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            node.next = self._head
            cur = self._head
            while cur.next != self._head:
                cur = cur.next

            cur.next = node
            self._head = node

    def append(self, item):
        """在尾部添加一个节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            cur = self._head
            # print(type(cur), cur.item, cur.next)
            while cur.next != self._head:
                cur = cur.next

            # print(cur.item)
            cur.next = node
            node.next = self._head

    def insert(self, pos, item):
        """指定位置pos添加节点"""
        if pos <= 0:
            self.add(item)
        elif pos > (self.length() - 1):
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            cur_pos = 0
            while cur.next != self._head:
                if (pos - 1) == cur_pos:
                    node.next = cur.next
                    cur.next = node
                    break
                cur_pos += 1
                cur = cur.next

    def remove(self, item):
        """删除一个节点"""
        if self.is_empty():
            return

        pre = self._head
        # 删除首节点
        if pre.item == item:
            cur = pre
            while cur.next != self._head:
                cur = cur.next

            cur.next = pre.next     # 删除首节点（跳过该节点）
            self._head = pre.next   # 重新指定首节点

        # 删除其他的节点
        else:
            cur = pre
            while cur.next != self._head:
                if cur.next.item == item:
                    cur.next = cur.next.next
                cur = cur.next

    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            return -1

        cur_pos = 0
        cur = self._head
        if cur.item == item:
            return cur_pos

        while cur.next != self._head:
            if cur.item == item:
                return cur_pos
            cur_pos += 1
            cur = cur.next

        if cur_pos == self.length() - 1:
            return -1


if __name__ == "__main__":
    ll = SinCycLinkedList()
    ll.add(1)       # 1
    ll.add(2)       # 2 1
    # ll.travel()
    ll.append(3)    # 2 1 3
    ll.insert(2, 4) # 2 1 4 3
    ll.insert(4, 5) # 2 1 4 3 5
    ll.insert(0, 6) # 6 2 1 4 3 5
    print("length:", ll.length())        # 6
    ll.travel()                           # 6 2 1 4 3 5
    print("search(3)", ll.search(3))     # 4
    print("search(7)", ll.search(7))     # -1
    print("search(6)", ll.search(6))    # 0
    print("remove(1)")
    ll.remove(1)
    print("length:", ll.length())       # 6 2 4 3 5
    print("remove(6)")
    ll.remove(6)
    ll.travel()

结果：
length: 6
6
2
1
4
3
5
search(3) 4
search(7) -1
search(6) 0
remove(1)
length: 5
remove(6)
2
4
3
5

 

双向链表：一种更复杂的链表是 "双向链表" 或 "双面链表"。每个节点有两个链接：一个指向前一个节点，当次节点为第一个节点时，指向空值；而另一个指向下一个节点，当此节点为最后一个节点时，指向空值。

class Node:
    """节点"""
    def __init__(self, item):
        self.item = item
        self.prev = None
        self.next = None


class DLinkList:
    """双向链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """获取链表长度"""
        if self.is_empty():
            return 0
        else:
            cur = self._head
            count = 1
            while cur.next is not None:
                count += 1
                cur = cur.next

            return count

    def travel(self):
        """遍历链表"""
        print("↓↓" * 10)
        if self.is_empty():
            print("")

        else:
            cur = self._head
            print(cur.item)
            while cur.next is not None:
                cur = cur.next
                print(cur.item)
        print("↑↑" * 10)

    def add(self, item):
        """链表头部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head

            node.next = cur
            cur.prev = node
            self._head = node

    def append(self, item):
        """链表尾部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
        else:
            cur = self._head
            # 遍历找到最后一个节点
            while cur.next is not None:
                cur = cur.next

            # 在尾节点添加新的节点
            cur.next = node
            node.prev = cur

    def insert(self, pos, item):
        """指定位置添加"""
        # 头部添加
        if pos <= 0:
            self.add(item)

        # 尾部添加
        elif pos > (self.length() - 1):
            self.append(item)

        # 其他位置添加
        else:
            node = Node(item)

            cur = self._head
            cur_pos = 0
            while cur.next is not None:
                if cur_pos == (pos - 1):
                    # 与下一个节点互相指向
                    node.next = cur.next
                    cur.next.prev = node
                    # 与上一个节点互相指向
                    cur.next = node
                    node.prev = cur
                cur_pos += 1
                cur = cur.next

    def remove(self, item):
        """删除节点"""
        if self.is_empty():
            return
        else:
            cur = self._head
            # 删除首节点
            if cur.item == item:
                self._head = cur.next
                cur.next.prev = None

            # 删除其他节点
            else:
                while cur.next is not None:
                    if cur.item == item:
                        # 删除之前：1 ←→ [2] ←→ 3
                        # 删除之后：1 ←→ 3
                        cur.prev.next = cur.next
                        cur.next.prev = cur.prev
                    cur = cur.next

                # 删除尾节点
                if cur.item == item:
                    cur.prev.next = None


    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            return -1
        else:
            cur = self._head
            cur_pos = 0
            while cur.next is not None:
                if cur.item == item:
                    return cur_pos

                cur_pos += 1
                cur = cur.next

            if cur_pos == (self.length() - 1):
                return -1


if __name__ == "__main__":
    ll = DLinkList()
    ll.add(1)       # 1
    ll.add(2)       # 2 1
    ll.append(3)    # 2 1 3
    ll.insert(2, 4) # 2 1 4 3
    ll.insert(4, 5) # 2 1 4 3 5
    ll.insert(0, 6) # 6 2 1 4 3 5
    print("length:", ll.length())   # 6
    ll.travel()                 # 6 2 1 4 3 5
    print("search(3)", ll.search(3))
    print("search(4)", ll.search(4))
    print("search(10)", ll.search(10))
    ll.remove(1)
    print("length:", ll.length())
    ll.travel()
    print("删除首节点 remove(6)：")
    ll.remove(6)
    ll.travel()
    print("删除尾节点 remove(5)：")
    ll.remove(5)
    ll.travel()
结果：
length: 6
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
6
2
1
4
3
5
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
search(3) 4
search(4) 3
search(10) -1
length: 5
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
6
2
4
3
5
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
删除首节点 remove(6)：
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
2
4
3
5
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
删除尾节点 remove(5)：
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
2
4
3
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑

 

栈数据结构只允许在一端进行操作，按照后进先出（LIFO，Last In First Out）。

栈结构的实现

# Author:song
class Stack(object):
    """栈"""
    def __init__(self):
        self._items = []

    def is_empty(self):
        """判断是否为空"""
        return self._items == []
    def push(self,item):
        """添加新元素到栈顶"""
        self._items.append(item)

    def pop(self):
        """弹出栈顶元素"""
        self._items.pop()

    def peek(self):
        """返回栈顶元素"""
        if self._items:
            return self._items[-1]
        else:
            return None
        pass
    def size(self):
        pass

if __name__=="__main__":
    s=Stack()
    print(s.is_empty())

 

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。一种先进先出（FIFO，First In First Out）的线性表

队列的实现

class Queue:
    """队列"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def enqueue(self, item):
        """添加元素"""
        self.items.insert(0, item)

    def dequeue(self):
        """从队列头部删除一个元素"""
        return self.items.pop()

    def size(self):
        return len(self.items)


if __name__ == "__main__":
    q = Queue()
    q.enqueue("hello")
    q.enqueue("world")
    q.enqueue("queue")
    print(q.size())
    print(q.dequeue())      # hello
    print(q.dequeue())      # world
    print(q.dequeue())      # queue

 

双端队列，是一种具有队列和栈的性质的数据结构。

class Deque:
    """双端队列"""
    def __init__(self):
        self.items = []

    def add_front(self, item):
        """从队头加入一个元素"""
        self.items.insert(0, item)

    def add_rear(self, item):
        """从队尾加入一个元素"""
        self.items.append(item)

    def remove_front(self):
        """从队头删除一个元素"""
        return self.items.pop(0)

    def remove_rear(self):
        """从队尾删除一个元素"""
        return self.items.pop()

    def is_empty(self):
        """是否为空"""
        return self.items == []

    def size(self):
        """队列长度"""
        return len(self.items)


if __name__ == "__main__":
    deque = Deque()
    deque.add_front(1)
    deque.add_front(2)
    deque.add_rear(3)
    deque.add_rear(4)
    print(deque.size())             # 4
    print(deque.remove_front())     # 2
    print(deque.remove_front())     # 1
    print(deque.remove_rear())      # 4
    print(deque.remove_rear())      # 3