集成学习之Boosting —— Gradient Boosting原理
集成学习之Boosting —— AdaBoost原理
集成学习之Boosting —— AdaBoost实现
集成学习之Boosting —— Gradient Boosting原理
集成学习之Boosting —— Gradient Boosting实现
集成学习之Boosting —— XGBoost
上一篇介绍了AdaBoost算法,AdaBoost每一轮基学习器训练过后都会更新样本权重,再训练下一个学习器,最后将所有的基学习器加权组合。AdaBoost使用的是指数损失,这个损失函数的缺点是对于异常点非常敏感,(关于各种损失函数可见之前的文章: 常见回归和分类损失函数比较),因而通常在噪音比较多的数据集上表现不佳。Gradient Boosting在这方面进行了改进,使得可以使用任何损失函数 (只要损失函数是连续可导的),这样一些比较robust的损失函数就能得以应用,使模型抗噪音能力更强。
Boosting的基本思想是通过某种方式使得每一轮基学习器在训练过程中更加关注上一轮学习错误的样本,区别在于是采用何种方式?AdaBoost采用的是增加上一轮学习错误样本的权重的策略,而在Gradient Boosting中则将负梯度作为上一轮基学习器犯错的衡量指标,在下一轮学习中通过拟合负梯度来纠正上一轮犯的错误。这里的关键问题是:为什么通过拟合负梯度就能纠正上一轮的错误了?Gradient Boosting的发明者给出的答案是:函数空间的梯度下降。
函数空间的的梯度下降
这里首先回顾一下梯度下降 (Gradient Descend)。机器学习的一大主要步骤是通过优化方法最小化损失函数\(L(\theta)\),进而求出对应的参数\(\theta\)。梯度下降是经典的数值优化方法,其参数更新公式:
Gradient Boosting 采用和AdaBoost同样的加法模型,在第m次迭代中,前m-1个基学习器都是固定的,即$$f_m(x) = f_{m-1}(x) + \rho_m h_m(x) \tag{1.2}$$
因而在第m步我们的目标是最小化损失函数 \(L(f) = \sum\limits_{i=1}^NL(y_i,f_m(x_i))\),进而求得相应的基学习器。若将\(f(x)\)当成参数,则同样可以使用梯度下降法:
对比式 (1.2)和 (1.3),可以发现若将\(h_m(x) \approx -\frac{\partial L(y,f_{m-1}(x))}{\partial f_{m-1}(x)}\),即用基学习器\(h_m(x)\)拟合前一轮模型损失函数的负梯度,就是通过梯度下降法最小化\(L(f)\) 。由于\(f(x)\)实际为函数,所以该方法被认为是函数空间的梯度下降。
负梯度也被称为“响应 (response)”或“伪残差 (pseudo residual)”,从名字可以看出是一个与残差接近的概念。直觉上来看,残差\(r = y-f(x)\)越大,表明前一轮学习器\(f(x)\)的结果与真实值\(y\)相差较大,那么下一轮学习器通过拟合残差或负梯度,就能纠正之前的学习器犯错较大的地方。
Gradient Boosting算法流程
初始化: \(f_0(x) = \mathop{\arg\min}\limits_\gamma \sum\limits_{i=1}^N L(y_i, \gamma)\)
for m=1 to M:
(a) 计算负梯度: \(\tilde{y}_i = -\frac{\partial L(y_i,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}, \qquad i = 1,2 \cdots N\)
(b) 通过最小化平方误差,用基学习器\(h_m(x)\)拟合\(\tilde{y_i}\),\(w_m = \mathop{\arg\min}\limits_w \sum\limits_{i=1}^{N} \left[\tilde{y}_i - h_m(x_i\,;\,w) \right]^2\)
(c) 使用line search确定步长\(\rho_m\),以使\(L\)最小,\(\rho_m = \mathop{\arg\min}\limits_{\rho} \sum\limits_{i=1}^{N} L(y_i,f_{m-1}(x_i) + \rho h_m(x_i\,;\,w_m))\)
(d) \(f_m(x) = f_{m-1}(x) + \rho_m h_m(x\,;\,w_m)\)输出\(f_M(x)\)
回归提升树
在Gradient Boosting框架中,最常用的基学习器是决策树 (一般是CART),二者结合就成了著名的梯度提升树 (Gradient Boosting Decision Tree, GBDT)算法。下面先叙述回归问题,再叙述分类问题。注意GBDT不论是用于回归还是分类,其基学习器 (即单颗决策树) 都是回归树,即使是分类问题也是将最后的预测值映射为概率。
决策树可以看作是一个分段函数,将特征空间划分为多个独立区域,在每个区域预测一个常数,如下图所示:
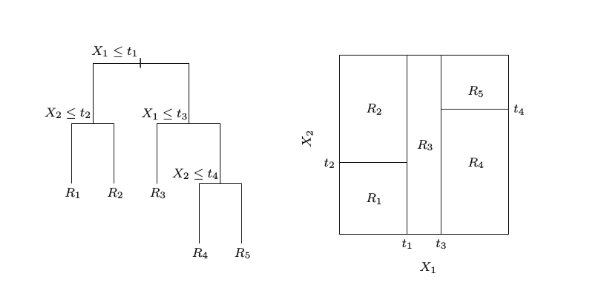
因此单棵决策树可表示为 \(h(x\,;\,\left \{R_j,b_j \right \}_1^J) = \sum \limits_{j=1}^J b_j I(x \in R_j)\),其中\(\left \{R_j \right \}_1^J\)为划分出来的独立区域 (即各个叶结点),\(\left \{ b_j \right \}_1^J\)为各区域上的输出值。为了求出这两个参数,于是上面Gradient Boosting中的2.b步变为:
即先求出树划分出的区域,而相应的\(b_{jm} = \mathop{mean} \limits_{x \in R_{jm}} \tilde{y}_{im}\)为该区域的平均值。
接下来注意到2.c步中求出的\(\rho_m\)对于整棵树中所有区域都是一样的,这样可能并不会使损失最小,因此Friedman提出可以对每个区域\(R_j\)分别求一个最优的值\(\gamma_{jm} = \rho_m b_{jm}\),则2.c步变为:
$$\gamma_{jm} = \mathop{\arg\min}\limits_\gamma \sum\limits_{x_i \in R_{jm}}L(y_i,f_{m-1}(x_i)+\gamma)$$
GBDT回归算法流程
初始化: \(f_0(x) = \mathop{\arg\min}\limits_\gamma \sum\limits_{i=1}^N L(y_i, \gamma)\)
for m=1 to M:
(a) 计算负梯度: \(\tilde{y}_i = -\frac{\partial L(y_i,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}, \qquad i = 1,2 \cdots N\)
(b) \(\left \{ R_{jm} \right\}_1^J = \mathop{\arg\min}\limits_{\left \{ R_{jm} \right\}_1^J}\sum\limits_{i=1}^N \left [\tilde{y}_i - h_m(x_i\,;\,\left \{R_{jm},b_{jm} \right\}_1^J) \right]^2\)
(c) \(\gamma_{jm} = \mathop{\arg\min}\limits_\gamma \sum\limits_{x_i \in R_{jm}}L(y_i,f_{m-1}(x_i)+\gamma)\)
(d) \(f_m(x) = f_{m-1}(x) + \sum\limits_{j=1}^J \gamma_{jm}I(x \in R_{jm})\)输出\(f_M(x)\)
回归问题损失函数的选择
常用的损失函数为平方损失 (squared loss),绝对值损失 (absolute loss),Huber损失 (huber loss),下面给出各自的负梯度 (来自ESL 360页):

分类提升树
将GBDT由回归拓展到分类,关键是损失函数的选择。如果选用了指数损失 (exponential loss),则退化为AdaBoost算法。另一种常用的分类损失函数为logistic loss,形式为\(L(y,f(x)) = log(1+e^{-2yf(x)})\) 。
要将其最小化,则对于\(f(x)\)求导并令其为0:
可以看到这与指数损失的目标函数一样,都是对数几率,见下图 (来自MLAPP 566页):

区别在于指数损失容易受异常点的影响,不够robust,且只能用于二分类问题。所以像scikit-learn中GradientBoostingClassifier的默认损失函数就是deviance。
与回归提升树的流程类似,求logistic loss的负梯度为:\(\tilde{y} = -\frac{\partial \, log(1+e^{-2yf(x)})}{\partial f(x)} = -\frac{-2y e^{-2yf(x)}}{1+e^{-2yf(x)}} = \frac{2y}{1+e^{2yf(x)}}\)
对于每个区域\(R_j\)的最优值为:\(\gamma_j = \mathop{\arg\min}\limits_\gamma \sum\limits_{x \in R_j} L(y,f_{m-1}(x)+\gamma) = \mathop{\arg\min}\limits_\gamma \sum \limits_{x \in R_j} log(1+e^{-2y(f_{m-1}(x)+\gamma)})\)
上式难以直接求出,因此常用近似值代替:
\(\gamma_j = \frac{\sum\limits_{x \in R_j}\tilde{y}}{\sum\limits_{x \in R_j}|\tilde{y}|(2-|\tilde{y}|)}\)
因为是分类问题,最后输出\(f_M(x)\)后要进行概率估计:设 \(P = P(y=1|x)\),
正则化 (Regularization)
1、Shrinkage
对每个基学习器乘以一个系数\(\,\nu\, (0 < \nu <1)\),使其对最终模型的贡献减小,从而防止学的太快产生过拟合。\(\nu\)又称学习率,即scikit-learn中的learning rate。于是上文的加法模型就从:
$$f_m(x) = f_{m-1}(x) + \rho_m h_m(x,;,w_m)$$
变为:
$$f_m(x) = f_{m-1}(x) + \nu \rho_m h_m(x,;,w_m)$$
一般\(\nu\)要和迭代次数M结合起来使用,较小的\(\nu\)意味着需要较大的M。ESL中推荐的策略是先将\(\nu\)设得很小 (\(\nu\) < 0.1),再通过early stopping选择M,不过现实中也常用cross-validation进行选择。
2、Early stopping
将数据集划分为训练集和测试集,在训练过程中不断检查在测试集上的表现,如果测试集上的准确率下降到一定阈值之下,则停止训练,选用当前的迭代次数M,这同样是防止过拟合的手段。
3、限制树的复杂度
不加限制完全生成的树同样可能会学的太快导致过拟合,因而通常对其进行预剪枝。常用的方法是限制树的深度(scikit-learn中的max_depth)等。
4、Subsampling
借用bootstrap的思想,每一轮训练时只使用一部分样本,不同点是这里的采样是无放回抽样,这个方法被称为Stochastic Gradient Boosting。对于单棵树来说,只使用一部分样本拟合会增加单棵树的偏差和方差,然而subsampling会使树与树之间的相关性减少,从而降低模型的整体方差,很多时候会提高准确性。
subsampling的另一个好处是因为只使用一部分样本进行训练,所以能显著降低计算开销。
特征重要性
单棵决策树的可解释性很强,GBDT则继承了这个优点。
对于单棵树T,用下式来衡量每个特征\(X_l\)的重要性:
其中\(J\)表示叶结点 (leaf node) 数量,\(J-1\)表示内部结点 (internal node) 数量,\(X_{v(t)}\)是与内部结点t相关联的分裂特征。对于每个内部结点t,用特征\(X_{v(t)}\)来模拟划分特征空间,得到一个分裂后的平方误差减少量,即\(\hat{i}^2_t\),最后将所有内部节点上的误差减少量加起来,就是特征\(X_l\)的重要性。总误差减少地越多,该特征就越重要。
对于M棵树的集成而言,特征重要性就是各棵树相应值的平均:
终末 —— 决策树和GBDT
Gradient Boosting算法理论上可以选择多种不同的学习算法作为基学习器,但实际使用地最多的无疑是决策树,这并非偶然。决策树有很多优良的特性,比如能灵活处理各种类型的数据,包括连续值和离散值;对缺失值不敏感;不需要做特征标准化/归一化;可解释性好等等,但其致命缺点是不稳定,导致容易过拟合,因而很多时候准确率不如其他算法。
决策树是非参数模型,这并不意味着其没有参数,而是在训练之前参数数量是不确定的,因此完全生长的决策树有着较大的自由度,能最大化地拟合训练数据。然而单颗决策树是不稳定的,样本数相同的训练集产生微小变动就能导致最终模型的较大差异,即模型的方差大,泛化性能不好。集成学习的另一代表Bagging是对付这个问题的一大利器 (详见前一篇文章Bagging与方差) 。而Bagging的拓展算法 —— 随机森林,通过在树内部结点的分裂过程中,随机选取固定数量的特征纳入分裂的候选项,这样就进一步降低了单模型之间的相关性,总体模型的方差也比Bagging更低。
另一方面,决策树和Gradient Boosting结合诞生了GBDT,GBDT继承了决策树的诸多优点,同时也改进了其缺点。由于GBDT采用的树都是复杂度低的树,所以方差很小,通过梯度提升的方法集成多个决策树,最终能够很好的解决过拟合的问题。然而Boosting共有的缺点为训练是按顺序的,难以并行,这样在大规模数据上可能导致速度过慢,所幸近年来XGBoost和LightGBM的出现都极大缓解了这个问题,后文详述。
Reference:
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine
- Friedman, J. Stochastic Gradient Boosting
- Friedman, J., Hastie, T. and Tibshirani, R. The Elements of Staistical Learning
/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号