集成学习之Boosting —— Gradient Boosting实现
Gradient Boosting的一般算法流程
初始化: \(f_0(x) = \mathop{\arg\min}\limits_\gamma \sum\limits_{i=1}^N L(y_i, \gamma)\)
for m=1 to M:
(a) 计算负梯度: \(\tilde{y}_i = -\frac{\partial L(y_i,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}, \qquad i = 1,2 \cdots N\)
(b) 通过最小化平方误差,用基学习器\(h_m(x)\)拟合\(\tilde{y_i}\),\(w_m = \mathop{\arg\min}\limits_w \sum\limits_{i=1}^{N} \left[\tilde{y}_i - h_m(x_i\,;\,w) \right]^2\)
(c) 使用line search确定步长\(\rho_m\),以使L最小,\(\rho_m = \mathop{\arg\min}\limits_{\rho} \sum\limits_{i=1}^{N} L(y_i,f_{m-1}(x_i) + \rho h_m(x_i\,;\,w_m))\)
(d) \(f_m(x) = f_{m-1}(x) + \rho_m h_m(x\,;\,w_m)\)输出\(f_M(x)\)
-
另外具体实现了early_stopping,回归,分类和分步预测 (stage_predict,见完整代码)。
-
Gradient Boostig一般有一个初始值存在,即上面第一步中的\(f_0(x)\),在实现的时候这个初始值是不能乘学习率的,因为乘的话等于变相改变了初始值,会产生一些意想不到的结果 (很不幸我就犯过这个错误 ~) 。
# 先定义各类损失函数,回归有squared loss、huber loss;分类有logistic loss,modified huber loss
def SquaredLoss_NegGradient(y_pred, y):
return y - y_pred
def Huberloss_NegGradient(y_pred, y, alpha):
diff = y - y_pred
delta = stats.scoreatpercentile(np.abs(diff), alpha * 100)
g = np.where(np.abs(diff) > delta, delta * np.sign(diff), diff)
return g
def logistic(p):
return 1 / (1 + np.exp(-2 * p))
def LogisticLoss_NegGradient(y_pred, y):
g = 2 * y / (1 + np.exp(1 + 2 * y * y_pred)) # logistic_loss = log(1+exp(-2*y*y_pred))
return g
def modified_huber(p):
return (np.clip(p, -1, 1) + 1) / 2
def Modified_Huber_NegGradient(y_pred, y):
margin = y * y_pred
g = np.where(margin >= 1, 0, np.where(margin >= -1, y * 2 * (1-margin), 4 * y))
# modified_huber_loss = np.where(margin >= -1, max(0, (1-margin)^2), -4 * margin)
return g
class GradientBoosting(object):
def __init__(self, M, base_learner, learning_rate=1.0, method="regression", tol=None, subsample=None,
loss="square", alpha=0.9):
self.M = M
self.base_learner = base_learner
self.learning_rate = learning_rate
self.method = method
self.tol = tol
self.subsample = subsample
self.loss = loss
self.alpha = alpha
def fit(self, X, y):
# tol为early_stopping的阈值,如果使用early_stopping,则从训练集中分出验证集
if self.tol is not None:
X, X_val, y, y_val = train_test_split(X, y, random_state=2)
former_loss = float("inf")
count = 0
tol_init = self.tol
init_learner = self.base_learner
y_pred = init_learner.fit(X, y).predict(X) # 初始值
self.base_learner_total = [init_learner]
for m in range(self.M):
if self.subsample is not None: # subsample
sample = [np.random.choice(len(X), int(self.subsample * len(X)), replace=False)]
X_s, y_s, y_pred_s = X[sample], y[sample], y_pred[sample]
else:
X_s, y_s, y_pred_s = X, y, y_pred
# 计算负梯度
if self.method == "regression":
if self.loss == "square":
response = SquaredLoss_NegGradient(y_pred_s, y_s)
elif self.loss == "huber":
response = Huberloss_NegGradient(y_pred_s, y_s, self.alpha)
elif self.method == "classification":
if self.loss == "logistic":
response = LogisticLoss_NegGradient(y_pred_s, y_s)
elif self.loss == "modified_huber":
response = Modified_Huber_NegGradient(y_pred_s, y_s)
base_learner = clone(self.base_learner)
y_pred += base_learner.fit(X_s, response).predict(X) * self.learning_rate
self.base_learner_total.append(base_learner)
'''early stopping'''
if m % 10 == 0 and m > 300 and self.tol is not None:
p = np.array([self.base_learner_total[m].predict(X_val) for m in range(1, m+1)])
p = np.vstack((self.base_learner_total[0].predict(X_val), p))
stage_pred = np.sum(p, axis=0)
if self.method == "regression":
later_loss = np.sqrt(mean_squared_error(stage_pred, y_val))
if self.method == "classification":
stage_pred = np.where(logistic(stage_pred) >= 0.5, 1, -1)
later_loss = zero_one_loss(stage_pred, y_val)
if later_loss > (former_loss + self.tol):
count += 1
self.tol = self.tol / 2
print(self.tol)
else:
count = 0
self.tol = tol_init
if count == 2:
self.M = m - 20
print("early stopping in round {}, best round is {}, M = {}".format(m, m - 20, self.M))
break
former_loss = later_loss
return self
def predict(self, X):
pred = np.array([self.base_learner_total[m].predict(X) * self.learning_rate for m in range(1, self.M + 1)])
pred = np.vstack((self.base_learner_total[0].predict(X), pred)) # 初始值 + 各基学习器
if self.method == "regression":
pred_final = np.sum(pred, axis=0)
elif self.method == "classification":
if self.loss == "modified_huber":
p = np.sum(pred, axis=0)
pred_final = np.where(modified_huber(p) >= 0.5, 1, -1)
elif self.loss == "logistic":
p = np.sum(pred, axis=0)
pred_final = np.where(logistic(p) >= 0.5, 1, -1)
return pred_final
class GBRegression(GradientBoosting):
def __init__(self, M, base_learner, learning_rate, method="regression", loss="square",tol=None, subsample=None, alpha=0.9):
super(GBRegression, self).__init__(M=M, base_learner=base_learner, learning_rate=learning_rate, method=method,
loss=loss, tol=tol, subsample=subsample, alpha=alpha)
class GBClassification(GradientBoosting):
def __init__(self, M, base_learner, learning_rate, method="classification", loss="logistic", tol=None, subsample=None):
super(GBClassification, self).__init__(M=M, base_learner=base_learner, learning_rate=learning_rate, method=method,
loss=loss, tol=tol, subsample=subsample)
if __name__ == "__main__":
# 创建数据集进行测试
X, y = datasets.make_regression(n_samples=20000, n_features=10, n_informative=4, noise=1.1, random_state=1)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
model = GBRegression(M=1000, base_learner=DecisionTreeRegressor(max_depth=2, random_state=1), learning_rate=0.1,
loss="huber")
model.fit(X_train, y_train)
pred = model.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test, pred))
print('RMSE: ', rmse)
X, y = datasets.make_classification(n_samples=20000, n_features=10, n_informative=4, flip_y=0.1,
n_clusters_per_class=1, n_classes=2, random_state=1)
y[y==0] = -1
X_train, X_test, y_train, y_test = train_test_split(X, y)
model = GBClassification(M=1000, base_learner=DecisionTreeRegressor(max_depth=1, random_state=1), learning_rate=1.0,
method="classification", loss="logistic")
model.fit(X_train, y_train)
pred = model.predict(X_test)
acc = np.zeros(pred.shape)
acc[np.where(pred == y_test)] = 1
accuracy = np.sum(acc) / len(pred)
print('accuracy logistic score: ', accuracy)
model = GBClassification(M=1000, base_learner=DecisionTreeRegressor(max_depth=1, random_state=1), learning_rate=1.0,
method="classification", loss="modified_huber")
model.fit(X_train, y_train)
pred = model.predict(X_test)
acc = np.zeros(pred.shape)
acc[np.where(pred == y_test)] = 1
accuracy = np.sum(acc) / len(pred)
print('accuracy modified_huber score: ', accuracy)
输出结果:
RMSE: 8.454462867923157
accuracy logistic score: 0.9434
accuracy modified_huber score: 0.9402
回归:
X, y = datasets.make_regression(n_samples=20000, n_features=20, n_informative=10, noise=100, random_state=1) # 数据集
下图比较了回归问题中使用平方损失和Huber损失的差别以及各自的early stopping point:

分类:
在分类问题中将上一篇中的 AdaBoost 和本篇中的GBDT作比较,仍使用之前的数据集,其中GBDT分别使用了logistic loss和 这篇文章 最后提到的modified huber loss:
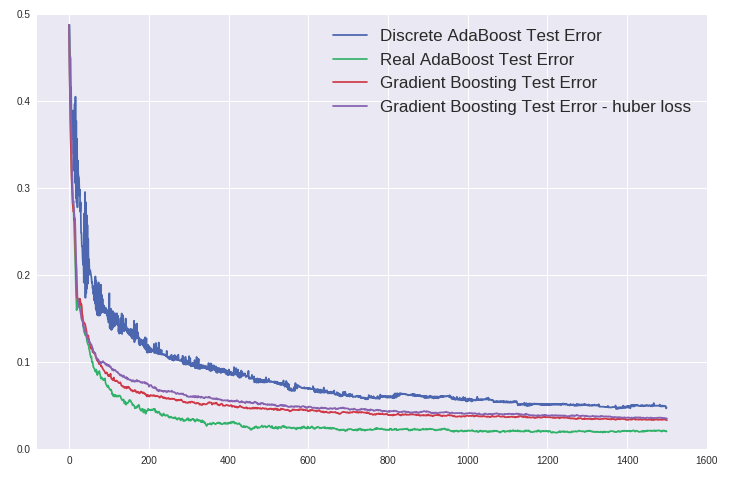
下面换一个噪音较大的数据集,用PCA降到二维进行可视化:
X, y = datasets.make_classification(n_samples=20000, n_features=10, n_informative=4, flip_y=0.3, n_clusters_per_class=1, n_classes=2, random_state=1)

这一次modified loss比logistic loss表现好,但都不如Real AdaBoost。

/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号