常见回归和分类损失函数比较

代码

损失函数的一般表示为\(L(y,f(x))\)，用以衡量真实值\(y\)和预测值\(f(x)\)之间不一致的程度，一般越小越好。为了便于不同损失函数的比较，常将其表示为单变量的函数，在回归问题中这个变量为\(y-f(x)\)，在分类问题中则为\(yf(x)\)。下面分别进行讨论。

回归问题的损失函数

回归问题中\(y\)和\(f(x)\)皆为实数\(\in R\)，因此用残差 \(y-f(x)\)来度量二者的不一致程度。残差 (的绝对值) 越大，则损失函数越大，学习出来的模型效果就越差（这里不考虑正则化问题）。


常见的回归损失函数有：

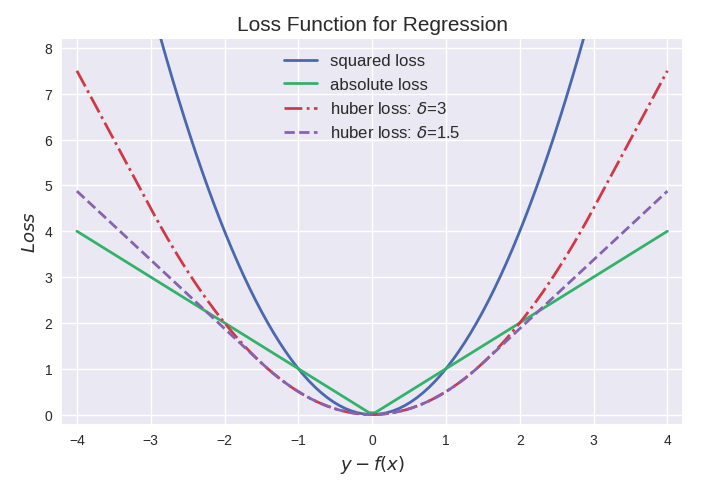
• 平方损失 (squared loss) ： \((y-f(x))^2\)
• 绝对值 (absolute loss) : \(|y-f(x)|\)
• Huber损失 (huber loss) : \(\left\{\begin{matrix}\frac12[y-f(x)]^2 & \qquad |y-f(x)| \leq \delta \\ \delta|y-f(x)| - \frac12\delta^2 & \qquad |y-f(x)| > \delta\end{matrix}\right.\)

其中最常用的是平方损失，然而其缺点是对于异常点会施以较大的惩罚，因而不够robust。如果有较多异常点，则绝对值损失表现较好，但绝对值损失的缺点是在$y-f(x)=0$处不连续可导，因而不容易优化。
Huber损失是对二者的综合，当$|y-f(x)|$小于一个事先指定的值$\delta$时，变为平方损失，大于$\delta$时，则变成类似于绝对值损失，因此也是比较robust的损失函数。三者的图形比较如下：

---

分类问题的损失函数

对于二分类问题，\(y\in \left\{-1,+1 \right\}\)，损失函数常表示为关于\(yf(x)\)的单调递减形式。如下图：

\(yf(x)\)被称为margin，其作用类似于回归问题中的残差 \(y-f(x)\)。


二分类问题中的分类规则通常为 \(\text{sign}(f(x)) = \left\{\begin{matrix} +1 \qquad\text{if}\;\;yf(x) \geq 0 \\ -1 \qquad \text{if} \;\; yf(x) < 0\end{matrix}\right.\)

可以看到如果 \(yf(x) > 0\)，则样本分类正确，\(yf(x) < 0\) 则分类错误，而相应的分类决策边界即为 \(f(x) = 0\)。所以最小化损失函数也可以看作是最大化 margin 的过程，任何合格的分类损失函数都应该对 margin<0 的样本施以较大的惩罚。

1、 0-1损失 (zero-one loss)

\[L(y,f(x)) = \left\{\begin{matrix} 0 \qquad \text{if} \;\; yf(x)\geq0 \\ 1 \qquad \text{if} \;\; yf(x) < 0\end{matrix}\right. \]

0-1损失对每个错分类点都施以相同的惩罚，这样那些“错的离谱“ (即 \(margin \rightarrow -\infty\))的点并不会收到大的关注，这在直觉上不是很合适。另外0-1损失不连续、非凸，优化困难，因而常使用其他的代理损失函数进行优化。

2、Logistic loss

\[L(y,f(x)) = log(1+e^{-yf(x)}) \]

logistic Loss为Logistic Regression中使用的损失函数，下面做一下简单证明：

Logistic Regression中使用了Sigmoid函数表示预测概率：$$g(f(x)) = P(y=1|x) = \frac{1}{1+e^{-f(x)}}$$

而$$P(y=-1|x) = 1-P(y=1|x) = 1-\frac{1}{1+e^{-f(x)}} = \frac{1}{1+e^{f(x)}} = g(-f(x))$$

因此利用\(y\in\left\{-1,+1\right\}\)，可写为\(P(y|x) = \frac{1}{1+e^{-yf(x)}}\)，此为一个概率模型，利用极大似然的思想：

​ $$max \left(\prod\limits_{i=1}^m P(y_i|x_i)\right) = max \left(\prod\limits_{i=1}^m \frac{1}{1+e^{-y_if(x_i)}}\right)$$

两边取对数，又因为是求损失函数，则将极大转为极小：

\[max\left(\sum\limits_{i=1}^m logP(y_i|x_i)\right) = -min \left(\sum\limits_{i=1}^m log(\frac{1}{1+e^{-y_if(x_i)}})\right) = min\left(\sum\limits_{i=1}^m log(1+e^{-y_if(x_i)}\right) \]

这样就得到了logistic loss。

如果定义\(t = \frac{y+1}2 \in \left\{0,1\right\}\)，则极大似然法可写为：

\[\prod\limits_{i=1}^m (P(t_i=1|x_i))^{t_i}((1-P(t_i=1|x))^{1-t_i} \]

取对数并转为极小得：

\[\sum\limits_{i=1}^m \big\{ -t_i\log P(t_i=1|x_i) - (1-t_i)\log (1-P(t_i=1|x_i))\big\} \]

上式被称为交叉熵损失 (cross entropy loss)，可以看到在二分类问题中logistic loss和交叉熵损失是等价的，二者区别只是标签y的定义不同。

3、Hinge loss

\[L(y,f(x)) = max(0,1-yf(x)) \]

hinge loss为svm中使用的损失函数，hinge loss使得\(yf(x)>1\)的样本损失皆为0，由此带来了稀疏解，使得svm仅通过少量的支持向量就能确定最终超平面。

hinge loss被翻译为“合页损失”，那么合页究竟长啥样？如图，确实有点像hinge loss的形状：

来看下 hinge loss 是如何推导出来的，带软间隔的svm最后的优化问题可表示为：

\[\begin{align} & \mathop{min}\limits_{\boldsymbol{w},b,\xi} \frac12 ||\boldsymbol{w}||^2 + C\sum\limits_{i=1}^m\xi_i \tag{1}\\ & s.t. \quad y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \geqslant 1 - \xi_i \tag{2}\\ & \qquad\;\;\;\xi_i \geqslant 0\; , \;\;\;\;i = 1,2,..., m \tag{3} \end{align} \]

\((2)\) 式重新整理为 $ \xi_i \geqslant 1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b)$ 。若 \(1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) < 0\) ，由于约束\((3)\) 的存在，则 \(\xi_i \geqslant 0\) ；若\(1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \geqslant 0\) ，则依然为 $ \xi_i \geqslant 1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b)$ 。所以\((2),(3)\) 式结合起来：

\[\xi_i \geqslant max(0,\, 1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b)) = max(0,\, 1-y_if(x_i)) \]

又由于 \((1)\) 式是最小化问题，所以取 \(\xi_i\) 的极小值，即令 \(\xi_i = max(0,1-yf(x))\) 代入 \((1)\) 式，并令\(\lambda = \frac{1}{2C}\) ：

\[min\; C\sum\limits_{i=1}^m max(0,\, 1-y_if(x_i)) + \frac12 ||\boldsymbol{w}||^2 \quad {\large \propto} \quad min\; \sum\limits_{i=1}^m \underbrace{max(0,\, 1-y_if(x_i))}_{hinge \; loss} + \lambda ||\boldsymbol{w}||^2 \]

另外可以看到 svm 这个形式的损失函数是自带参数 \(\boldsymbol{w}\) 的\(L2\) 正则的，而相比之下Logistic Regression的损失函数则没有显式的正则化项，需要另外添加。

4、指数损失(Exponential loss)

\[L(y,f(x)) = e^{-yf(x)} \]

exponential loss为AdaBoost中使用的损失函数，使用exponential loss能比较方便地利用加法模型推导出AdaBoost算法 (具体推导过程)。然而其和squared loss一样，对异常点敏感，不够robust。

5、modified Huber loss

\[L(y,f(x)) = \left \{\begin{matrix} max(0,1-yf(x))^2 \qquad if \;\;yf(x)\geq-1 \\ \qquad-4yf(x) \qquad\qquad\;\; if\;\; yf(x)<-1\end{matrix}\right.\qquad \]

modified huber loss结合了hinge loss和logistic loss的优点，既能在\(yf(x) > 1\)时产生稀疏解提高训练效率，又能进行概率估计。另外其对于\((yf(x) < -1)\) 样本的惩罚以线性增加，这意味着受异常点的干扰较少，比较robust。scikit-learn中的SGDClassifier同样实现了modified huber loss。

最后来张全家福：

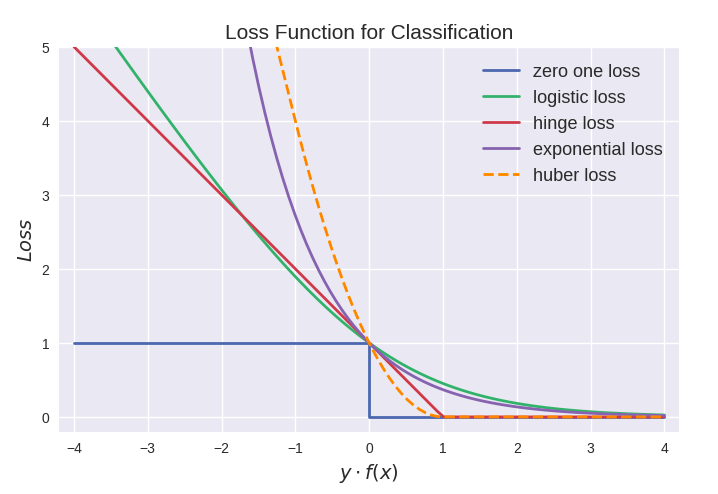
从上图可以看出上面介绍的这些损失函数都可以看作是0-1损失的单调连续近似函数，而因为这些损失函数通常是凸的连续函数，因此常用来代替0-1损失进行优化。它们的相同点是都随着\(margin \rightarrow -\infty\)而加大惩罚；不同点在于，logistic loss和hinge loss都是线性增长，而exponential loss是以指数增长。

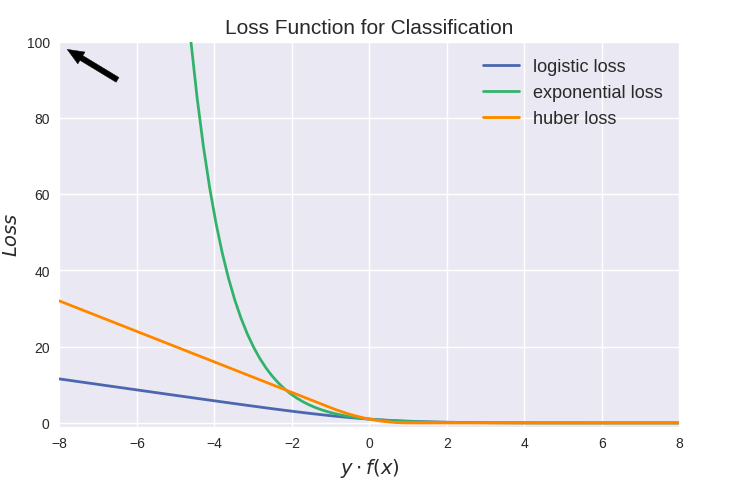
值得注意的是上图中modified huber loss的走向和exponential loss差不多，并不能看出其robust的属性。其实这和算法时间复杂度一样，成倍放大了之后才能体现出巨大差异：

/