拉格朗日乘子法 - KKT条件 - 对偶问题
拉格朗日乘子法 - KKT条件 - 对偶问题
支持向量机 (一): 线性可分类 svm
支持向量机 (二): 软间隔 svm 与 核函数
支持向量机 (三): 优化方法与支持向量回归
接下来准备写支持向量机,然而支持向量机和其他算法相比牵涉较多的数学知识,其中首当其冲的就是标题中的拉格朗日乘子法、KKT条件和对偶问题,所以本篇先作个铺垫。
大部分机器学习算法最后都可归结为最优化问题。对于无约束优化问题: \(\min\limits_\boldsymbol{x} f(\boldsymbol{x})\) (本篇为形式统一,只考虑极小化问题),一般可直接求导并用梯度下降或牛顿法迭代求得最优值。
对于含有等式约束的优化问题,即:
由于等式约束 \(h_i(\boldsymbol{x}) = 0\) 的存在,无法直接求导迭代求解。拉格朗日乘子法是解决此类问题的常用方法,其核心思想是将约束优化转化为无约束优化问题,即将有 \(d\) 个变量和 \(m\) 个等式约束条件的最优化问题转换为一个有 \((d + m)\) 个变量的函数求平稳点的问题。
拉格朗日乘子法
下面画图来直观理解拉格朗日乘子法,先看下左图: 黑色虚线为函数 \(f(x)\) 的等值线,红色实线为约束条件 \(h(x) = 0\) ,这里的关键是 \(f(x)\) 在极小点处必然与 \(h(x) = 0\) 相切,如下左图相切于黄色点 \(x_1\) 。为什么这么说?来看下右图: 如果 \(f(x)\) 与 \(h(x) = 0\) 不相切,则相交于两个黄色点,而由于 \(x\) 是连续的,则必然能找到一个新的 \(x_2\) 使得 \(f(x_2)\) 更小,图中表示为蓝色虚线,使得在 \(x_2\) 处 \(f(x)\) 与 \(h(x) = 0\) 相切。
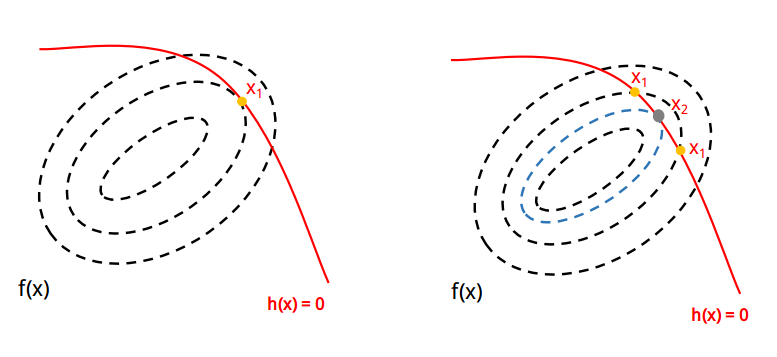
由于相交的两个黄色点不是极小点,梯度 \(\nabla f(x_1)\) 仍然会沿着 \(h(x) = 0\) 变化,因而在这两个点 \(\nabla f(x_1)\) 不与 \(h(x) = 0\) 的切线方向垂直,只有在极小点才会正交。
由此可以得出两个推论 (见下图):
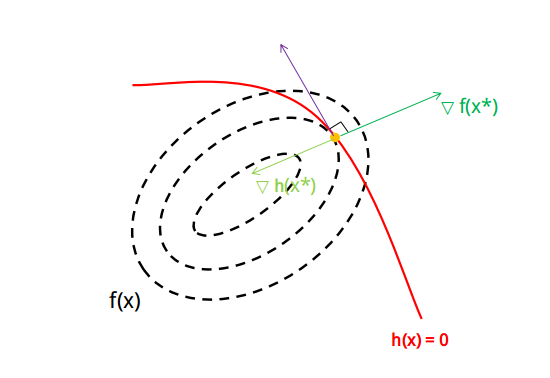
(1). 对于 \(f(\boldsymbol{x})\) 的极小点 \(\boldsymbol{x}^*\) ,\(f(\boldsymbol{x})\) 在 \(\boldsymbol{x}^*\) 处的梯度 \(\nabla f(\boldsymbol{x}^*)\) 与 \(h(\boldsymbol{x}) = 0\) 的切线方向垂直
(2). 对于 \(f(\boldsymbol{x})\) 的极小点 \(\boldsymbol{x}^*\) ,\(h(\boldsymbol{x})\) 在 \(\boldsymbol{x}^*\) 处的梯度 \(\nabla h(\boldsymbol{x}^*)\) 与 \(h(\boldsymbol{x}) = 0\) 的切线方向垂直
对于第 (2) 点,可作如下证明: 设 \(\boldsymbol{x}(t)\) 为连续可微的函数,则有 \(h(\boldsymbol{x}(t)) = 0\) ,利用链式法则:
\(\frac{\text{d}{\boldsymbol{x}(t)}}{\text{d}t}\) 即为切线方向,所以本质上 \(h(\boldsymbol{x}) = 0\) 上任意一点的梯度 \(\nabla h(\boldsymbol{x})\) 都与其正交,\(\boldsymbol{x}^*\) 自然也不例外。
于是可以得出在极小点处 \(\nabla h(\boldsymbol{x}^*)\) 与 \(\nabla f(\boldsymbol{x}^*)\) 平行,即存在 \(\lambda \neq 0\) ,使得:
\(\lambda\) 被称为拉格朗日乘子,下面定义拉格朗日函数:
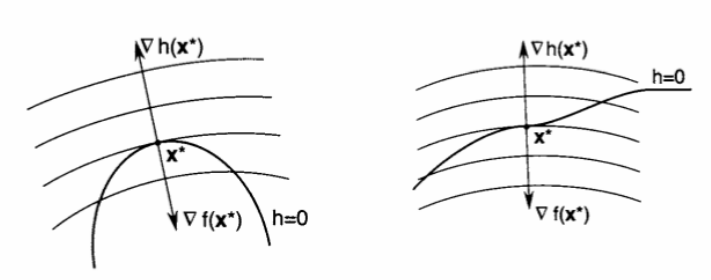
将上式分别对 \(\boldsymbol{x}\) 和 \(\lambda\) 求导置零,就分别得到 \((1.1)\) 式和等式约束 \(h(\boldsymbol{x}) = 0\) ,这样就将原约束优化问题转化为对 \(\mathcal{L}(\boldsymbol{x}, \lambda)\) 的无约束优化问题。 然而这个方法找出来的平稳点不一定都是原问题的极值点,如下左图是一个极值点,而下右图却不是极值点。
KKT 条件
上面拉格朗日乘子法解决的是等式约束优化问题,而对于不等式约束优化问题也可解,只不过要加一些附加条件:
先下一个定义:
对于一个不等式约束 \(g_j(\boldsymbol{x}) \leqslant 0\) ,若在 \(\boldsymbol{x}^*\) 处 \(g_j(\boldsymbol{x}^*) < 0\) ,那么称该不等式约束是 \(\boldsymbol{x}^*\) 处的不起作用约束;若在 \(\boldsymbol{x}^*\) 处 \(g_j(\boldsymbol{x}^*) = 0\) ,那么称该约束是 \(\boldsymbol{x}^*\) 处的起作用约束。
对于该定义的直观解释见下图: 灰色部分为约束 \(g(\boldsymbol{x}) \leqslant 0\) 的可行域,若最优点 \(\boldsymbol{x}^*\) 在区域内 (下左图,\(g(\boldsymbol{x}) < 0\) ) ,则约束并没有起到”约束的作用“,这样可直接通过 \(\nabla f(\boldsymbol{x}) = 0\) 来获得最优点,这等价于让 \((1.1)\) 式中 \(\lambda = 0\) 。
若最优点 \(\boldsymbol{x}^*\) 在区域边界上 (下右图,\(g(\boldsymbol{x}) = 0\) ) ,那么对于 \(f(\boldsymbol{x})\) 来说,在 \(\boldsymbol{x}^*\) 处是外部较大,内部较小,因为越靠近等值线中心 \(f(\boldsymbol{x})\) 越小; 而对于 \(g(\boldsymbol{x})\) 来说,在 \(\boldsymbol{x}\) 处的变化趋势是内部较小,外部较大,因为在内部 \(g(\boldsymbol{x}) \leqslant 0\) ,外部 \(g(\boldsymbol{x}) > 0\) 。这样 \(\nabla f(\boldsymbol{x}^*)\) 和 \(\nabla g(\boldsymbol{x}^*)\) 的方向必相反,此时 \(g(\boldsymbol{x}) = 0\), 那么套用 \((1.1)\) 式可得 \(\lambda > 0\) 。
综合这两种情况:
这被称为互补松弛条件 (\(\text{complementary slackness}\)) 。

由此推广到多个约束,定义广义拉格朗日函数:
\(\boldsymbol{\alpha} \geqslant 0\) 为 KKT 乘子,\(\boldsymbol{\beta}\) 为拉格朗日乘子,其最优解满足:
\((1) \sim (2)\) 式为原问题的约束条件,\((3) \sim (4)\) 式上文定义中已证明。这就是不等式约束优化问题的 KKT 条件 (\(\text{Karush-Kuhn-Tucker Condition}\)),KKT 条件是拉格朗日乘子法在不等式约束优化问题上的泛化。KKT 条件是极小点的必要条件,即满足 KKT 条件不一定是极小点,但极小点必满足 KKT 条件。
对偶问题
将原始问题转化为对偶问题是求解带约束优化问题的一种方法,当然这不是唯一的方法,只不过转化为对偶问题后往往更容易求解,因而被广为应用。
设原始优化问题为:
其拉格朗日函数为 \(\mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) =f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} g_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \beta_{j} h_{j}(\boldsymbol{x}), \;\;\alpha \geqslant 0\) 。若 \(\boldsymbol{x}\) 违反了一些约束 (即存在 \(i,j\) 使得 \({g_{i}(\boldsymbol{x}) \geqslant 0}\) 或 \(h_j(\boldsymbol{x}) \neq 0\) ) ,那么 \(\max\limits_{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = \infty\) ,则:
这样原始优化问题 \((3.1)\) 就等价于:
接下来定义 \((3.1)\) 式的对偶问题 (dual problem) 为:
对偶问题是原始问题的下界,即:
上式为什么成立?因为任意值小于等于最大值,所以对于任意 \(\boldsymbol{\alpha}, \,\boldsymbol{\beta}\) ,\(\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \; \leq \; \min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) ,如果上式恒成立,则不等式左边的 \(\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) 的极大值 \(\max _{\boldsymbol{\alpha}, \boldsymbol{\beta}}\min _{\boldsymbol{x}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) 一定小于等于 不等式右边的 \(\min _{\boldsymbol{x}} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})\) ,这就是所谓的 ”极小的极大 \(\leqslant\) 极大的极小“ 。
\((3.2)\) 式是不等式,所以该性质被称为弱对偶性 (weak duality)。若要等式成立,则为强对偶性 (strong duality),需要满足 slater 条件:
\(\text{slater}\) 条件: 原始问题为凸优化问题,即 \(f(\boldsymbol{x})\),\(g(\boldsymbol{x})\) 为凸函数,\(h(\boldsymbol{x})\) 为仿射函数,且可行域中至少有一点使不等式约束严格成立时,强对偶性成立,对偶问题等价于原始问题。
最后,利用强对偶性求出的 \(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}\) 同时也是原始问题的最优解,所以依然满足 KKT 条件:
/




