题解 P1801 【黑匣子_NOI导刊2010提高(06)】
蒟蒻来发题解了。我仔细看了一下其他题解,各位巨佬用了堆,红黑树,splay,treap之类的强大算法,表示蒟蒻的我只会口胡这些算法,所以我决定用一种极其易理解的算法————fhq treap,作为treap的升级版,它不仅好理解,好用,还能做到可持久化,真是神级算法(不知道为什么会fhq treap的我,不会一般treap)
进入正题,首先我先讲讲fhq treap的主要思想,它是一种非旋转的平衡树,不用考虑左旋右旋等麻烦情况,它很暴力,直接靠拆树,合并来实现,有点二分的感觉,其实它很多操作就有二分思想。
好了,看图,我们有一颗二叉树
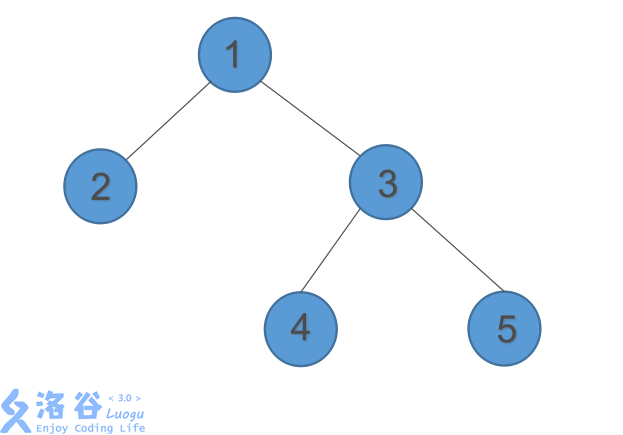
当我们插入6号,发现它失衡了
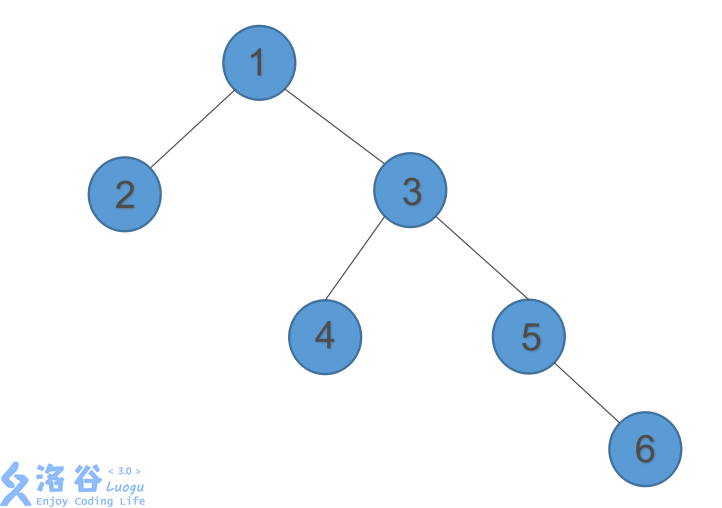
多西太?大丈夫
我们不用旋转,不用交换,直接拆。
第一个重要操作:拆树(split),我们先把树分为x,y两部分,x的节点权值≤k, y的节点的权值>k,要插入一个数a的话,就把新的节点a看做是一棵树,先与x合并,合并完之后将合并的整体与y合并
上代码
1 inline void split(int &x,int &y,int k,int pos) 2 { 3 if(!pos)x=y=0;//root=0时(即第一次split) 此时的x=?,y=?很明显要给他们初始化 即x=0,y=0 4 else 5 { 6 if(val[pos]<=k) 7 {x=pos;split(son[pos][2],y,k,son[pos][2]);} 8 else 9 {y=pos;split(x,son[pos][1],k,son[pos][1]);} 10 update(pos); 11 } 12 }
第二个重要操作:合并(merge) 还是两棵树x,y。如果rand[x]<rand[y] 我们就把y接在x的右儿子上 你想如果接在左儿子 那左儿子的权值就大于父亲的权值了 不符合二叉搜索树的性质
反之同理
其实merge 要理解的话自己画两颗treap 然后模拟一下。
上代码
1 inline int merge(int x,int y) 2 { 3 if(x==0||y==0) return x+y;//第一次合并的情况 4 if(rnd[x]<rnd[y]) 5 { 6 son[x][2]=merge(son[x][2],y); 7 update(x);return x; 8 } 9 else 10 { 11 son[y][1]=merge(x,son[y][1]); 12 update(y);return y; 13 } 14 }
至于查排名(find),就是easy的操作了,根据堆的性质,直接找右子树大小,再去遍历就好了,不知道的可以先去学习二叉搜索树的操作(各位巨佬肯定都会了)
ac代码
1 #include<iostream> 2 #include<cstdio> 3 #include<ctime> 4 #include<cstdlib> 5 #include<cstring> 6 #include<algorithm> 7 #define maxn 200010 8 using namespace std; 9 int n,val[maxn],rnd[maxn],son[maxn][3],size[maxn],sum_p,m; 10 //val记录权值,son记录左右子树大小,size[i]记录以i为根节点的树的大小 11 int X1[maxn]; 12 int flag[maxn]; 13 inline void read(int &x)//快读 14 { 15 x=0;int f=1; 16 char ch=getchar(); 17 while(ch<'0'||ch>'9') 18 {if(ch=='-') f=-1; ch=getchar();} 19 while(ch>='0'&&ch<='9') 20 {x=x*10+ch-'0';ch=getchar();} 21 x*=f; 22 } 23 inline int newnode(int x) 24 { 25 ++sum_p;size[sum_p]=1; 26 val[sum_p]=x;rnd[sum_p]=rand(); 27 return sum_p; 28 } 29 inline void update(int x) 30 { 31 size[x]=size[son[x][1]]+size[son[x][2]]+1;//加上自己 32 } 33 inline void split(int &x,int &y,int k,int pos)//x,左子树的根(权值较小的),y,右子树的根,pos为现在的节点 34 { 35 if(!pos)x=y=0;//root=0时(即第一次split) 此时的x=?,y=?所以初始化x=0,y=0 36 else 37 { 38 if(val[pos]<=k) 39 {x=pos;split(son[pos][2],y,k,son[pos][2]);} 40 else 41 {y=pos;split(x,son[pos][1],k,son[pos][1]);} 42 update(pos); 43 } 44 } 45 inline int merge(int x,int y)//保证y子树权值大于x子树 46 { 47 if(x==0||y==0) return x+y;//第一次合并的情况 48 if(rnd[x]<rnd[y]) //比rand大小 49 { 50 son[x][2]=merge(son[x][2],y); 51 update(x);return x; 52 } 53 else 54 { 55 son[y][1]=merge(x,son[y][1]); 56 update(y);return y; 57 } 58 } 59 inline int find(int pos,int rank) 60 { 61 while(1) 62 { 63 if(size[son[pos][1]]>=rank) 64 { 65 pos=son[pos][1]; 66 } 67 else 68 if(size[son[pos][1]]+1==rank)return pos;//由于是儿子 要加上自己 69 else 70 { 71 rank-=size[son[pos][1]]+1; 72 pos=son[pos][2]; 73 } 74 } 75 } 76 int main() 77 { 78 srand((unsigned)time(NULL)); 79 int a,b,x,y,z,op,root=0,pos=0; 80 read(n),read(m); 81 for(register int i=1;i<=n;i++) 82 read(X1[i]); 83 for(register int i=1;i<=m;i++) 84 {read(op);flag[op]++;}//记录查询点 85 for(register int i=1;i<=n;i++) 86 { 87 split(x,y,X1[i],root); 88 root=merge(merge(x,newnode(X1[i])),y); 89 while(flag[i]>=1)//可能一个位置不止一次查询 90 { 91 pos++;flag[i]--; 92 printf("%d\n",val[find(root,pos)]); 93 } 94 } 95 }
最后我再给没学过fhq treap的同学补充一点基础操作
1、求a的排名:我们只需要split成一颗≤a-1,一颗≥a的就行了 a的排名就是第一棵treap的size+1;
2、求a前驱:以a-1为界限拆树就好了,a的前驱肯定就是第一个treap里最大的 ,就在find操作的基础上,在x里找排名为size[x]的
3、求a后继:以a为界限拆树,a的后继是第二个treap里最小的;
4、delete和区间反转就留给大家自己思考了,无论如何,fhq treap的操作基本上都建立在拆树与合并上。
最后强烈安利一波fhq treap


 浙公网安备 33010602011771号
浙公网安备 33010602011771号