关于Ciarlet的泛函的一道homework的一个想法

【转载请注明出处】http://www.cnblogs.com/mashiqi

2016/11/21

 

有一道题是证明$(\mathbb{R}^n,\|\cdot\|_p)$当$p : 1< p <+\infty$时是uniformly convex的。这个题当然可以用Clarkson定理证明出来。可是我觉得这个结论非常的显然，但居然还要用到像Clarkson这样复杂麻烦的东西。一定有一个简单的方法可以证明出来。当然，我没有找到什么简单的方法，可是我觉得这个Claim应该成立：

对任意的$p : 1< p <+\infty$，都存在一个只依赖于$p$和$n$的正实数$C(n,p)$，使得下式对所有$a, b \in \mathbb{R}^n$都成立：

$$|\frac{a+b}{2}|^p + C(n,p) \cdot |\frac{a-b}{2}|^p \leq \frac{1}{2}|a|^p + \frac{1}{2}|b|^p$$

 

为此，我做了如下MATLAB仿真：

clear;
n = 2; % dimension
steps = 0.01;
epsilon = 0.1;
p = (1:steps:3) + steps; % adjust the range of this argument
np = length(p);
nRep = 1e3;
c = zeros(np,nRep);
for i = 1:np % p
    for j = 1:nRep % repeat
        pp = p(i);
        a = randn(n,1);
        b = randn(n,1);
        while (norm(a-b,pp) < epsilon)
            a = randn(n,1);
            b = randn(n,1);
        end
        c(i,j) = ( 0.5 * norm(a,pp)^pp + 0.5 * norm(b,pp)^pp - norm((a+b)/2,pp)^pp ) / norm((a-b)/2,pp)^pp;
    end
end

c_max = max(c,[],2);
plot(p,c_max'); title(strcat('dimension =',{' '},num2str(n)));

结果如下：

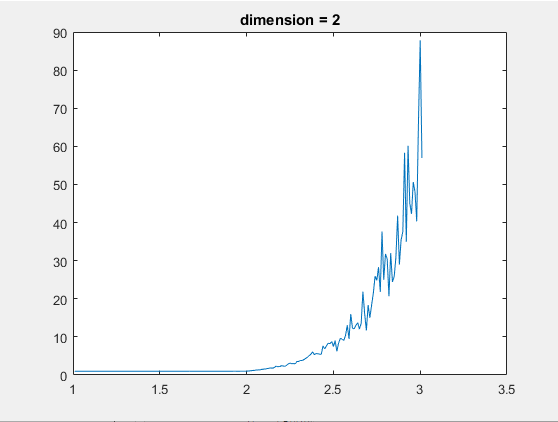
我觉得这个结论应该是成立的，虽然不知道怎么证明。