滑动窗口相关的题目总结
关于滑动窗口的题目,大概有两类,一类是“子串”问题;一类是“用单调队列来解决”的问题
一、“子串问题”
https://labuladong.gitbook.io/algo/bi-du-wen-zhang/hua-dong-chuang-kou-ji-qiao-jin-jie
labuladong大佬在这里总结了滑动窗口这类问题的代码框架,很实用。
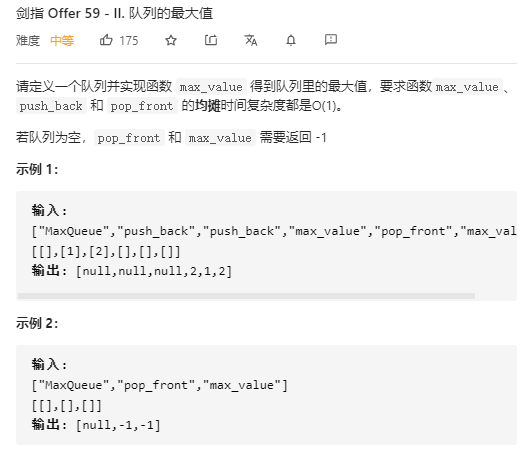
二、“用单调队列来解决”的问题
class MaxQueue { queue<int> q; // 队列 deque<int> d; // 双端队列,构造单调队列 public: MaxQueue() { } int max_value() { if (d.empty()) { return -1; } return d.front(); } void push_back(int value) { while (!d.empty() && d.back() < value) { d.pop_back(); // 插入的同时维护单调队列 } d.push_back(value); // 加入单调队列 q.push(value); // 加入队列 } int pop_front() { if (q.empty()) { return -1; } int ans = q.front(); if (ans == d.front()) { // 判断移除的队列中的元素是不是单调队列的头部,如果是的话二者都要移除 d.pop_front(); } q.pop(); return ans; // 返回pop出的那个数 } }; /** * Your MaxQueue object will be instantiated and called as such: * MaxQueue* obj = new MaxQueue(); * int param_1 = obj->max_value(); * obj->push_back(value); * int param_3 = obj->pop_front(); */

class Solution { public: vector<int> maxSlidingWindow(vector<int>& nums, int k) { vector<int> maxInWindow; // 记录结果 if (nums.size() >= k && k >= 1) { // 如果数组的长度大于窗口的大小并且窗口至少长度为1才有意义 deque<int> index; // 创建一个队列,只把有可能成为窗口中最大值的数值存入 for (int i=0; i<k; i++) { // 未形成窗口 while (!index.empty() && nums[i] >= nums[index.back()]) { // index.pop_back(); // 队列中递减排列,因为最大的滑出后,下一个第二大的有可能成为下一个窗口的最大值 } index.push_back(i); // 存下标的目的是知道滑动窗口是否包含一个数组中的数字 } for (int i=k; i<nums.size(); i++) { // 已经形成窗口 maxInWindow.push_back(nums[index.front()]); // 队列首部的肯定是最大值 if (!index.empty() && index.front() <= (int)(i-k)) { // 当一个数字的下标与当前处理的数字的下标之差大于或者等于滑动窗口的打小时,这个数字已经从窗口中滑出了 index.pop_front(); // 在头部删除 } while (!index.empty() && nums[i] >= nums[index.back()]) { // 将下一个要进来窗口中的数放到合适的位置 index.pop_back(); // 在尾部删除 } index.push_back(i); } maxInWindow.push_back(nums[index.front()]); // 最后一个窗口的最大值 } return maxInWindow; } };



