构造二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        //要先明白，构造一颗二叉树，首先你得构造出根节点吧，然后你再去构造左右子节点
        //根节点简单，就是前序遍历的第一个元素，很容易能够构造
        //关键是你要构造左右子节点以及往下的，你得知道哪些元素是左子树哪些是右子树的，这就需要通过中序序列和已知的根节点的值来确定，这是中序的特性
        return build(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
    }
    TreeNode* build(vector<int> preorder, int prestart, int preend, vector<int> inorder, int instart, int inend)
    {
        if(prestart > preend)
            return nullptr;
        //先保存根节点的值，找到中序序列中根节点的位置
        int rootval = preorder.at(prestart);
        int index = 0;
        for(int i=instart;i<=inend;i++)
        {
            if(inorder.at(i) == rootval)
            {
                index = i;
                break;
            }
        }
        //以上找到了中序序列中根节点的位置index
        int leftSize = index - instart;//得到左子树节点的个数，因为要分开前序遍历序列
        //先构造根节点
        TreeNode* root = new TreeNode(rootval);
        //递归构造
        root->left = build(preorder, prestart+1, index+leftSize, inorder, instart, index-1);
        root->right = build(preorder, prestart+leftSize+1, preend, inorder, index+1, inend);
        return root;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
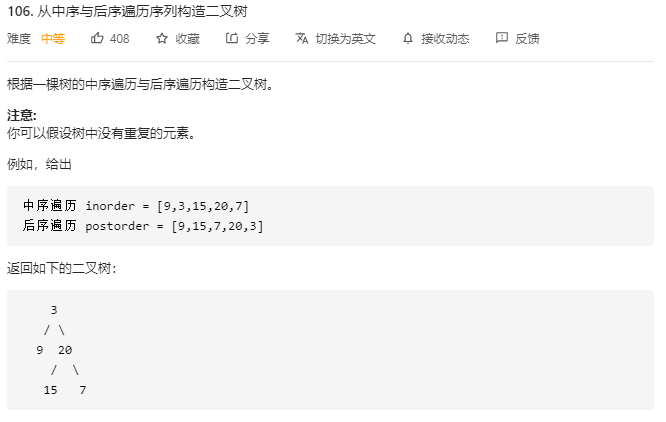
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        //后序和中序跟前一个一样的道理，还是应该先构造头结点，然后递归构造左右子树
        //需要新建一个函数进行数组起止位置控制，别的也没什么
        //后序最后一个是根节点的值
        return build(inorder, 0, inorder.size()-1, postorder, 0, postorder.size()-1);
    }
    TreeNode* build(vector<int>& inorder, int inStart, int inEnd, vector<int>& postorder, int postStart, int postEnd)
    {
        //base case
        if(inStart > inEnd)
            return nullptr;
        //先保存根节点的值
        int rootVal = postorder.at(postEnd);
        int index = 0;//记录中序序列中根节点的位置
        for(int i=inStart;i<=inEnd;i++)
        {
            if(inorder.at(i) == rootVal)
            {
                index = i;
                break;
            }
        }
        int leftSize = index - inStart;
        //构造根节点
        TreeNode* root = new TreeNode(rootVal);
        //递归构造左右子树
        root->left = build(inorder, inStart, index-1, postorder, postStart, postStart+leftSize-1);
        root->right = build(inorder, index+1, inEnd, postorder, postStart+leftSize, postEnd-1);
        return root;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
       return build(nums, 0, nums.size()-1);
    }
    TreeNode* build(vector<int>& nums, int lo, int hi) {
        //终止条件
        if(lo > hi) {
            return nullptr;
        }
        
        //找到数组中的最大值，和最大值的索引，注意下面循环的起止值是lo和hi，不是从0开始
        int maxNum = INT_MIN;
        int index = -1;
        for(int i=lo; i<=hi; i++) {
            if(nums[i] > maxNum) {
                maxNum = nums[i];
                index = i;
            }
        }

        //构造最大节点（根节点）
        TreeNode* head = new TreeNode(maxNum);
        //递归构造左右子节点
        head->left = build(nums, lo, index-1);
        head->right = build(nums, index+1, hi);

        return head;
    }
};