求二叉树的节点个数总结

对于让你求二叉树节点个数的题目，无非就是普通二叉树、完全二叉树、满二叉树三种。这三者的关系是，二叉树>完全二叉树>满二叉树。

如果是题目没有给限定条件，只让你求二叉树的节点个数，则按照普通二叉树来求；如果给了限定条件，完全二叉树或者满二叉树，则根据他们的特性有更优化的算法。

一、求普通二叉树的节点个数

递归算法和迭代算法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        //用递归的方式,用递归真的太简单了
        //if(root == NULL)
        //    return 0;
        //return 1+countNodes(root->left)+countNodes(root->right);//属于后序遍历，先求了子树的，然后加上了中间的根节点
        //还可以采用层序遍历的方式，稍微改动模板，其实前序后序中序遍历感觉都行
        if(root == NULL)
            return 0;
        queue<TreeNode*> que;
        que.push(root);
        int result = 0;
        while(!que.empty()) {
            int size = que.size();
            for(int i=0; i<size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if(node->left)
                    que.push(node->left);
                if(node->right)
                    que.push(node->right);
                result++;
            }
        }
        return result;
    }
};

着重说一下这种递归算法的时间复杂度是O(n)

二、求满二叉树的节点个数

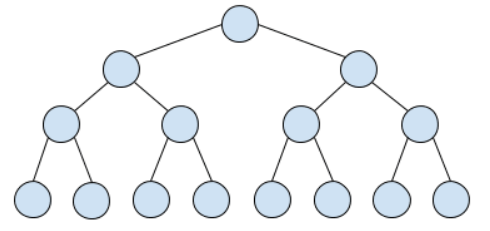
满二叉树也是普通二叉树，用求普通二叉树节点个数的方法完全能够得到正确答案，但是我们一开始说了，既然给定了这个条件，我们就能根据它的特性得到简单的解法。

满二叉树的节点个数是跟二叉树的深度有关系的，节点个数n=2^(深度)-1，根据这个特性，我们只需要知道二叉树的深度，就能得到节点个数。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        int h = 0;
        //计算树的高度
        while(root!=nullptr) {
            root = root->left;
            h++;
        }
        return (int)math.pow(2,h)-1;
    }
};

while循环只需要logN的时间，所以时间复杂度为O(logN)。

三、求完全二叉树的节点个数

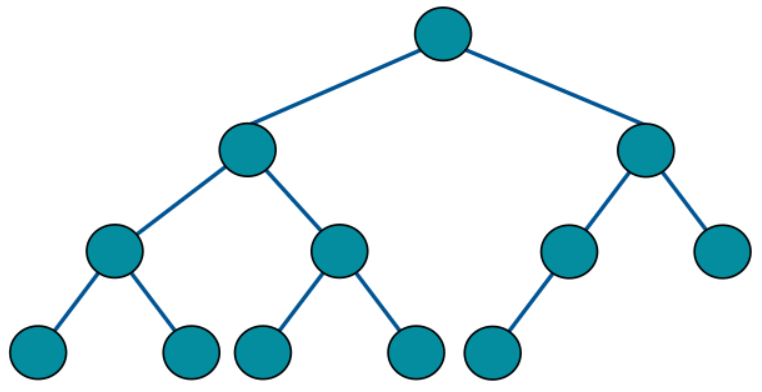
完全二叉树也是普通二叉树，用求普通二叉树节点个数的方法完全能够得到正确答案，但是我们一开始说了，既然给定了这个条件，我们就能根据它的特性得到简单的解法。

完全二叉树的的两棵子树，至少有一颗是满二叉树。既然有这个特点，那这棵满二叉树就可以节省时间，另一棵当做普通二叉树计算。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        TreeNode* leftNode = root;
        TreeNode* rightNode = root;
        //得到左右子树的高度
        int lh=0, rh=0;
        while(leftNode != nullptr) {
            leftNode = leftNode->left;
            lh++;
        }
        while(rightNode != nullptr) {
            rightNode = rightNode->right;
            rh++;
        }
        //如果左右子树的高度相同，说明是一棵满二叉树
        if(lh == rh)
            return pow(2,lh)-1;
        //如果高度不相等，按照普通二叉树的计算逻辑
        return 1+countNodes(root->left)+countNodes(root->right);
    }
};

这个算法的时间复杂度为O(logNlogN)。因为while循环的时间是O(logN)，递归的时候因为上面提到的特性，只会递归一支子树，递归深度就是树的高度O(logN)，所以总体的时间复杂度是O(logNlogN)。