栈与队列

队列：先进先出

栈：先进后出

几个基础的问题：

1. C++中stack 是容器么？
2. 我们使用的stack是属于那个版本的STL？
3. 我们使用的STL中stack是如何实现的？
4. stack 提供迭代器来遍历stack空间么？

栈和队列和C++STL里面的两个数据结构。

 

 

 

 栈：先进后出

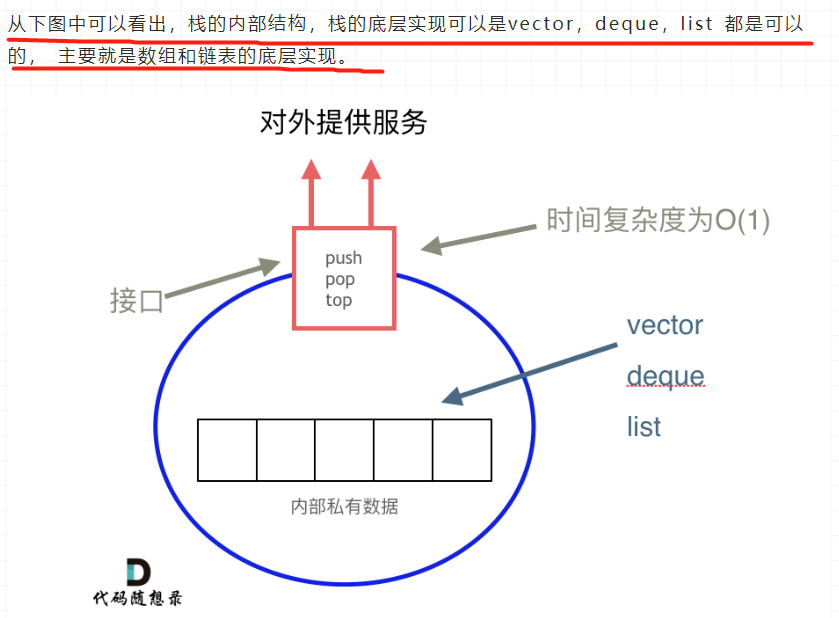
栈提供push、pop等接口，所有元素必须符合先进后出规则，所以栈不提供走访功能，也不提供迭代器iterator，不像是set或者是map提供迭代器来遍历所有元素。

「栈是以底层容器完成其所有的工作，对外提供统一的接口，底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。」

所以STL中栈往往不被归类为容器，而被归类为container adapter(容器适配器)

 

 「我们常用的SGI STL，如果没有指定底层实现的话，默认是以deque为缺省情况下栈的低层结构。」

deque是一个双向队列，只要封住一段，只开通另一端就可以实现栈的逻辑了。

「SGI STL中 队列底层实现缺省情况下一样使用deque实现的。」

我们也可以指定vector为栈的底层实现

队列 先进先出的数据结构，同样不允许有遍历行为，不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。

也可以指定list 为起底层实现

所以STL中队列也不被归类为容器，而被归类为container adapter（ 容器适配器）。

 

可以用栈来实现队列：两个栈可以实现队列！

class MyQueue {
public:
    stack<int> stIn;
    stack<int> stOut;
    /** Initialize your data structure here. */
    MyQueue() {

    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        stIn.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        if(stOut.empty()) {
            while(!stIn.empty()) {
                stOut.push(stIn.top());
                stIn.pop();
            }
        }
        int result = stOut.top();
        stOut.pop();
        return result;
    }
    
    /** Get the front element. */
    int peek() {
        int res = this->pop();//这里弹出了res
        stOut.push(res);
        return res;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return (stOut.empty() && stIn.empty());
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue* obj = new MyQueue();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->peek();
 * bool param_4 = obj->empty();
 */

可以用队列还实现栈！

class MyStack {
public:
    queue<int>que1;
    queue<int>que2;//用来备份的
    /** Initialize your data structure here. */
    MyStack() {

    }
    
    /** Push element x onto stack. */
    void push(int x) {
        que1.push(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        //现在元素都在que1里，队尾的元素是需要pop的元素，需要把其他的都暂存到que2里
        int size = que1.size();
        size--;
        while(size--) {
            que2.push(que1.front());
            que1.pop();
        }
        int result = que1.front();
        que1.pop();
        que1 = que2;//恢复que1
        while(!que2.empty())
            que2.pop();
        return result;
    }
    
    /** Get the top element. */
    int top() {
        return que1.back();
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return que1.empty();
    }
};

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

一个经典应用就是“有效的括号”问题。

 逆波兰表达式问题是栈的经典应用，也是一道比较难的题目，题目一定要记住一个规则：遇到数字则入栈；遇到算符则取出两个数字进行计算，并将结果压入栈中。

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> st;
        for(int i=0; i<tokens.size(); i++) {
            if(tokens[i]=="+" || tokens[i]=="-" || tokens[i]=="*" || tokens[i]=="/") {//这里一定要注意是双引号
                int num1 = st.top();
                st.pop();
                int num2 = st.top();
                st.pop();
                if(tokens[i]=="+")
                    st.push(num1+num2);
                else if(tokens[i]=="-")
                    st.push(num2-num1);//这里一定要注意相减的顺序
                else if(tokens[i]=="*")
                    st.push(num1*num2);
                else//除法
                    st.push(num2/num1);//这里一定要注意相除的顺序
            }
            else
                st.push(stoi(tokens[i]));
        }
        int result = st.top();
        st.pop();
        return result;
    }
};