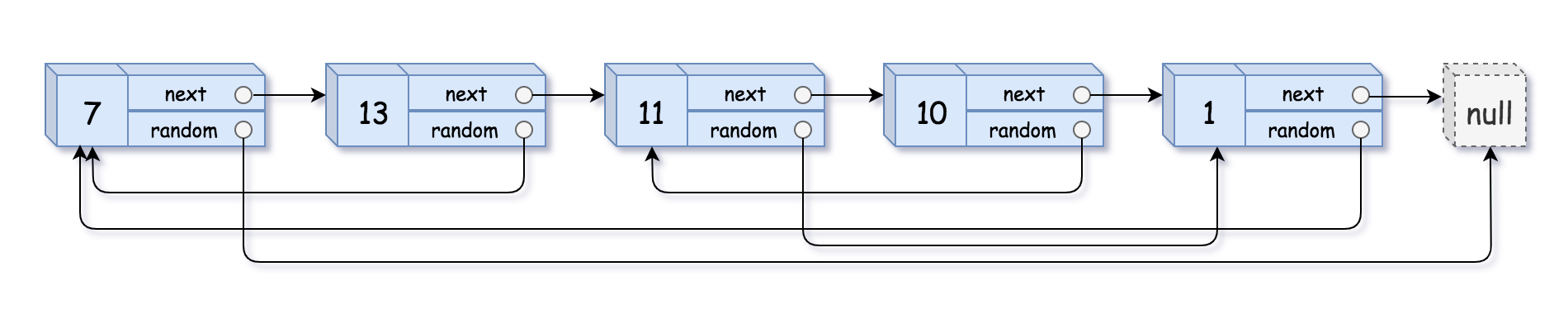
leetcode -- 递归法
人理解循环,神理解递归。递归不同于回溯,回溯是一种算法思路,递归是一种思路的实现方式,递归相当于图结构中的邻接矩阵和邻接表。这种实现方式通俗来说就是自己调用自己,比如,我想学习一下Spring cloud,但是在学习Spring cloud之前,我还得先学一下spring Boot,在学习SpringBoot之前,我先得学一下SpringMVC,学习SpringMVC之前,我还得先学习Spring,学习Spring之前,我先学习servlet,在学习serlvet之前,我先得学一下java,学完了java,我就可以依次学习servlet,Spring,SpringMVC,SpringBoot,SpringCloud,这个例子中学习就是一个递归函数,这个递归函数的终止条件是学完java。
因此在考虑递归算法的时候,首先需要考虑的是
- 递归函数应该做什么,
- 每一层递归的操作是什么,
- 递归的结束条件是什么。
当然递归的难也是在这三个问题的考虑之上,如何设计完美的递归函数还需要看各种题型。本文中的代码都在我的github。
回溯法多用于解决子集和需要列举全部情况的题目中,在本文中我将之分为:
- 顺序回溯,这种情况下多用于解决子集问题。
- 全路径回溯,这种情况下多用于解决列举全部组合的问题。
全路径递归
leetcode, 第509题目,Fibonacci Number,
The Fibonacci numbers, commonly denoted
F(n)form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from0and1. That is,F(0) = 0, F(1) = 1 F(n) = F(n - 1) + F(n - 2), for n > 1.Given
n, calculateF(n).Example 1:
Input: n = 2 Output: 1 Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.Example 2:
Input: n = 3 Output: 2 Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.Example 3:
Input: n = 4 Output: 3 Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.Constraints:
0 <= n <= 30
斐波那契数是入门经典的一道题目,也是递归思路非常清晰的一种思路,后面的每一项数字都是前俩项数字的和,这句话表明了每一层递归应该是前俩项相加,而递归结束条件就是n成为0或者1的时候。
// 递归法,但是效果差
public int fib(int n) {
if(n == 1 || n == 0) {
return n;
}
return fib(n-1) + fib(n-2);
}
这种写法在leetcode中效果不好,运行时间是6ms,只能超过32%的人,先思考一下效果差是因为什么?我们可以看一下计算5的斐波那契数过程。
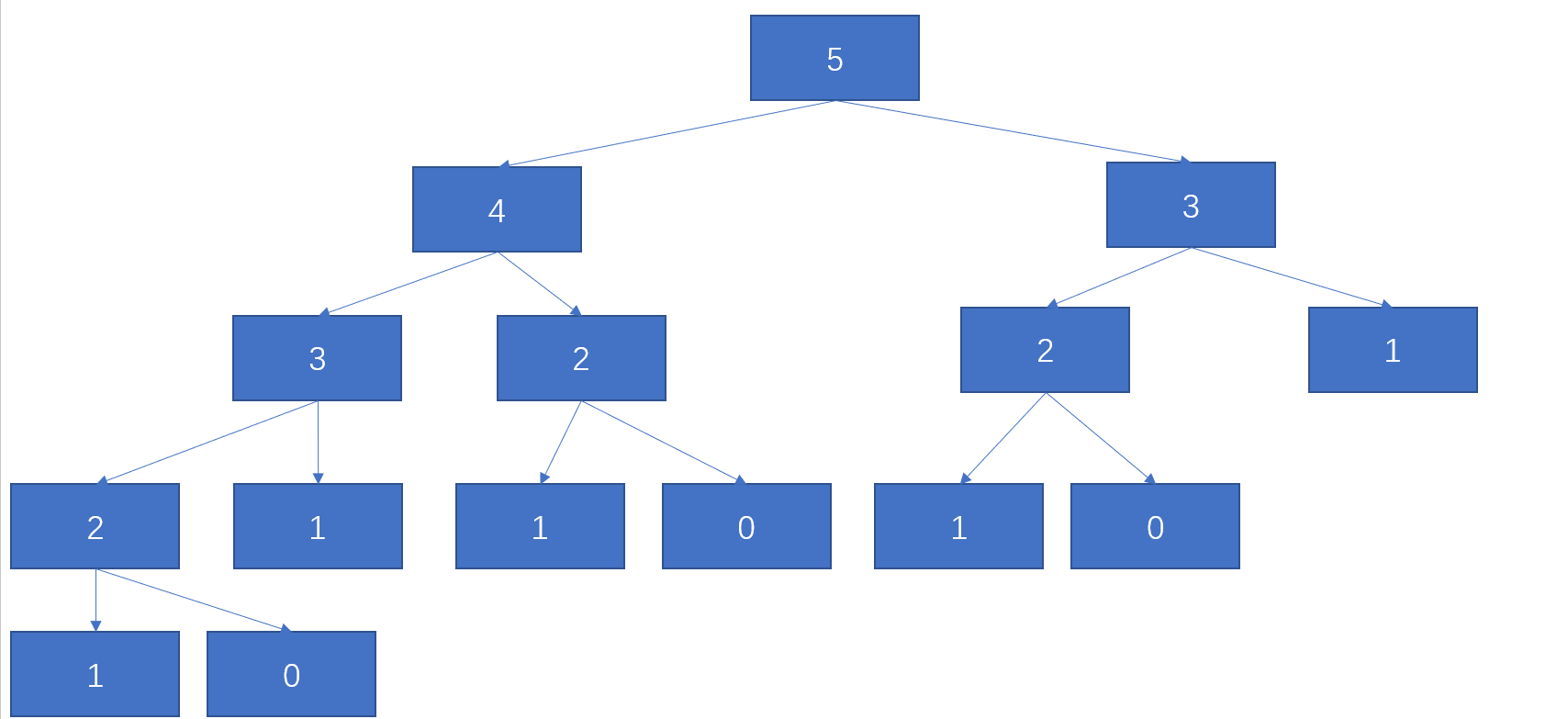
从中我们发现递归过程中有着大量的重复计算,4的前俩项是3,2,那么就需要递归计算3,但是在计算5的时候,也是需要计算3的,其中3就被重复计算了俩次,2被重复计算了3次。如果n很大,那么其中的重复计算也有很多很多,要想消去这些重复计算,最直接的想法就是记忆化递归,记忆化递归的思路下面再说,其实就是记录每次计算的值。
有着记忆功能的还有最令人头疼的动态规划,斐波那契数的计算也是可以通过动态规划来解决的。与递归由顶自下不同,动态规划是由底自上来做,动态规划需要考虑是状态变量、边界条件和状态转移方程。初始的状态变量就是0和1,状态转移方程就是斐波那契方程。
// 动态规划,速度很快
public int fib_1(int n) {
if(n == 1 || n == 0) {
return n;
}
int[] dp = new int[n+1];
dp[1] = 1;
for(int index = 2; index < n + 1; ++index) {
dp[index] = dp[index - 1] + dp[index - 2];
}
return dp[n];
}
动态规划不需要进行重复的计算,因此速度很快,在leetcode的运行时间是0ms。之后在记忆化递归的时候,我们还需要再讨论一下这道题,这道题也是可以使用记忆化递归来做的。
leetcode,第344题,Reverse String,
Write a function that reverses a string. The input string is given as an array of characters
s.Example 1:
Input: s = ["h","e","l","l","o"] Output: ["o","l","l","e","h"]Example 2:
Input: s = ["H","a","n","n","a","h"] Output: ["h","a","n","n","a","H"]Constraints:
1 <= s.length <= 105s[i]is a printable ascii character.Follow up: Do not allocate extra space for another array. You must do this by modifying the input array in-place with
O(1)extra memory.
反转字符串,最简单的办法使用for循环,直接每次交换首尾字符即可
// 要注意特殊情况,也就是[4,4,4,1,4]
public void reverseString(char[] s) {
if(s.length < 2) {
return ;
}
int start = 0;
int end = s.length - 1;
while(start < end) {
char temp = s[start];
s[start++] = s[end];
s[end--] = temp;
}
}
上面这种解法的时间复杂度已经很好了,但是如果非要将之改造成递归算法来做呢?需要考虑的是每层递归应该是交换字符,递归结束条件是首尾索引一样,递归的时间复杂度与上面解法的时间复杂度都是差不多的。
// 递归写法
public void reverseString(char[] s) {
if(s.length < 2) {
return ;
}
reverse(s,0,s.length - 1);
}
private void reverse(char[] s, int start, int end) {
if(start >= end) {
return;
}
reverse(s,start + 1,end - 1);
char temp = s[start];
s[start] = s[end];
s[end] = temp;
}
leetcode,第95题,Unique Binary Search Trees II,
Given an integer
n, return all the structurally unique BST's (binary search trees), which has exactlynnodes of unique values from1ton. Return the answer in any order.Example 1:
Input: n = 3 Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]Example 2:
Input: n = 1 Output: [[1]]Constraints:
1 <= n <= 8
这道题是需要求出所有的二叉搜索树,并且需要将几个二叉搜索树都输出。我们可以先从给定一个数输出这个数的其中一个二叉搜索树入手,根节点就是中心点,那么这道题就是简单的递归建树。
// 从构建一棵树进行思考
public TreeNode getTree(int n) {
return useGetTree(1,n);
}
private TreeNode useGetTree(int start, int end) {
if(start > end) {
return null;
}
int middle = start + (end - start)/2;
TreeNode root = new TreeNode(middle);
root.left = useGetTree(start, middle - 1);
root.right = useGetTree(middle + 1, end);
return root;
}
输出多棵树与上面的输出一棵树,最大的不同就是根节点是不同,输出多棵树需要遍历所有的值,并将每个值都作为根节点的值,之后得到左子树和右子树的多颗子树,这个时候只要将左子树的多颗子树和右子树的多颗子树进行组合,那么得到的就是我们所需要的多棵树。
// 从递归的方法来看生成多棵树
public List<TreeNode> generateTrees(int n) {
return useGetTree_1(1,n);
}
private List<TreeNode> useGetTree_1(int start, int end) {
List<TreeNode> all_trees = new ArrayList<>();
if(start > end) {
all_trees.add(null);
return all_trees;
}
for(int value = start; value <= end; ++value) {
List<TreeNode> left_node = useGetTree_1(start,value - 1);
List<TreeNode> right_node = useGetTree_1(value + 1,end);
for(int left_index = 0; left_index < left_node.size(); ++left_index) {
for(int right_index = 0; right_index < right_node.size(); ++right_index) {
TreeNode root = new TreeNode(value);
root.left = left_node.get(left_index);
root.right = right_node.get(right_index);
all_trees.add(root);
}
}
}
return all_trees;
}
上面的递归解法是可以变成动态规划的,不过动态规划的值不再是整数了,而是列表,列表中就是当前结点数为n的情况下所有的子树,和上面的递归一样,左右子树进行组合,不过这里需要注意的是,右子树的值是大于根节点的,动态数组中的值并不能直接用于构建右子树,我们需要将它与根节点的值相加。
// 对上面的递归进行动态规划改写
public List<TreeNode> generateTrees_1(int n) {
ArrayList<TreeNode>[] dp = new ArrayList[n+1];
dp[0] = new ArrayList<>();
if(n < 1) {
return dp[n];
}
dp[0].add(null);
for(int index = 1; index <= n; ++index) {
dp[index] = new ArrayList<TreeNode>();
for(int root_index = 1; root_index <= index; ++root_index) {
int left_num = root_index - 1;
int right_num = index - root_index;
for(TreeNode left_node:dp[left_num]) {
for(TreeNode right_node:dp[right_num]) {
TreeNode root = new TreeNode(root_index);
root.left = left_node;
// 不能直接使用,这是因为dp中的树是有值的,这个值与右子树是不同的
root.right = chooseRight(right_node,root_index);
dp[index].add(root);
}
}
}
}
return dp[n];
}
private TreeNode chooseRight(TreeNode right_node,int root_index) {
if(right_node == null) {
return right_node;
}
TreeNode new_right = new TreeNode(right_node.val + root_index);
new_right.left = chooseRight(right_node.left, root_index);
new_right.right = chooseRight(right_node.right, root_index);
return new_right;
}
如果我们以插入结点角度来看待这个动态规划问题,当我们要求三个结点的二叉搜索树的时候,我们可以往俩个结点的二叉搜索树中插入3,插入的3应该是树中最大值,那么这个新插入值一定是在俩个结点的所有二叉搜索树的根节点或者右边,只要依次对根节点,右子树右节点进行插入即可,当然要注意的是用来插入的树应该重新深拷贝一份。
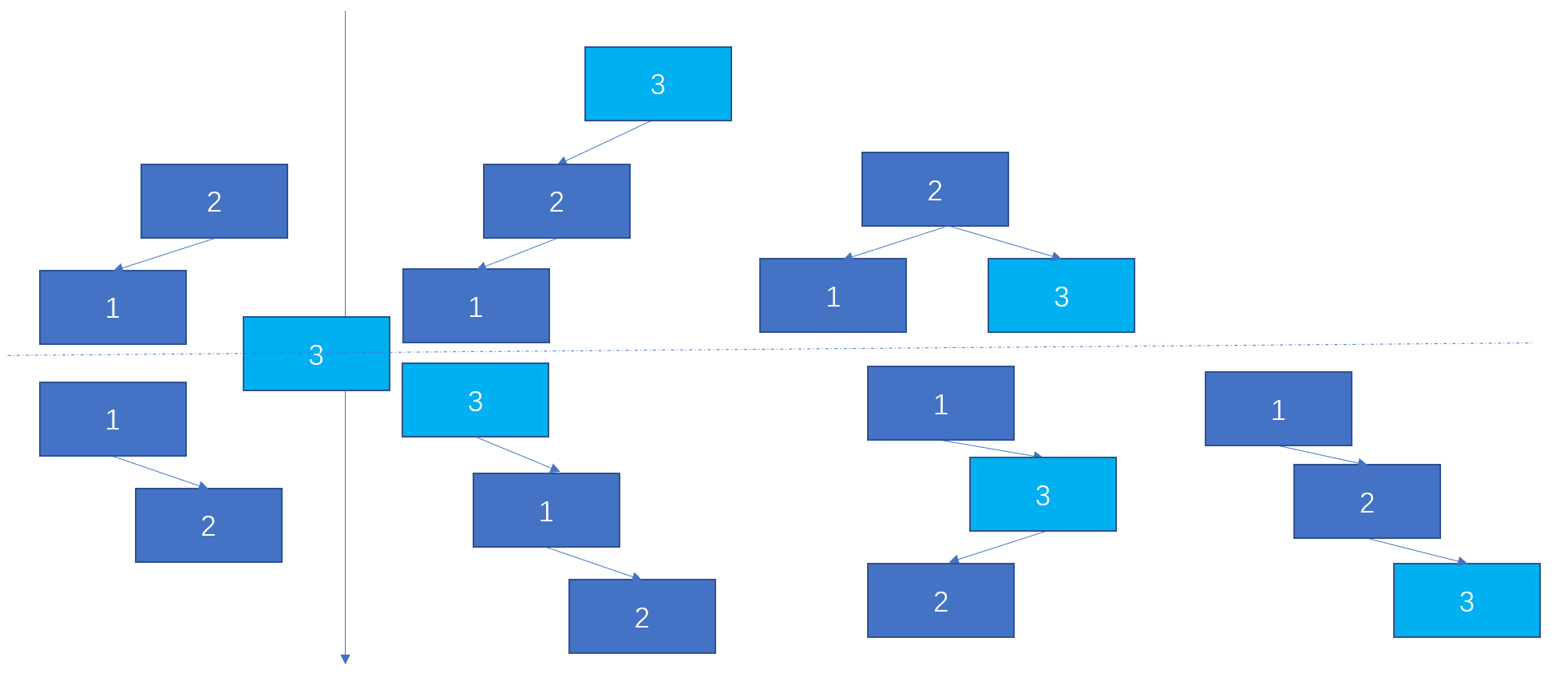
// 另一种动态规划的思想
public List<TreeNode> generateTrees_2(int n) {
List<TreeNode> pre_tree = new ArrayList<>();
if(n < 1) {
return pre_tree;
}
pre_tree.add(null);
for(int index = 1; index <= n; ++index) {
List<TreeNode> curr_tree = new ArrayList<>();
// 遍历之前所有的解
for(TreeNode one_pre:pre_tree) {
// 新增的数作为根节点
TreeNode curr_root = new TreeNode(index);
curr_root.left = one_pre;
curr_tree.add(curr_root);
// 下面就是将新增的数作为右子树中
for(int right_height = 0; right_height < index; ++right_height) {
// 首先需要重新复制一份
TreeNode tree_temp = treeCopy(one_pre);
TreeNode right_pos = tree_temp;
for(int right_index = 0; right_index < right_height; ++right_index) {
if(right_pos == null) {
break;
}
right_pos = right_pos.right;
}
// 还得再检查一次是否为null
if(right_pos == null) {
break;
}
// 进行插入
TreeNode new_right = new TreeNode(index);
new_right.left = right_pos.right;
right_pos.right = new_right;
curr_tree.add(tree_temp);
}
}
pre_tree = curr_tree;
}
return pre_tree;
}
private TreeNode treeCopy(TreeNode one_pre) {
if(one_pre == null) {
return one_pre;
}
TreeNode root = new TreeNode(one_pre.val);
root.left = treeCopy(one_pre.left);
root.right = treeCopy(one_pre.right);
return root;
}
记忆化递归
leetcode, 第509题目,Fibonacci Number,
The Fibonacci numbers, commonly denoted
F(n)form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from0and1. That is,F(0) = 0, F(1) = 1 F(n) = F(n - 1) + F(n - 2), for n > 1.Given
n, calculateF(n).Example 1:
Input: n = 2 Output: 1 Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.Example 2:
Input: n = 3 Output: 2 Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.Example 3:
Input: n = 4 Output: 3 Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.Constraints:
0 <= n <= 30
在全路径递归中,我们分析过这道题,这道题目最大的问题就是重复计算太多,因此使用递归思想的时候,我们需要解决这个重复计算太多的问题,最有效的办法就是记录,每层递归都要检查一下这个数是否被计算过,如果没有被计算过,那么进行递归计算,递归计算完成之后记录下来,如果被计算过,那么直接返回计算结果。
这其中主要思路还是和以前一样的,就是用什么数据结构来记录,我们需要记录俩个值,一个是被计算的数,一个是计算结果,那就使用键值对map来记录。
// 记忆化递归,使用map进行记录
public int fib_2(int n) {
if(n == 1 || n == 0) {
return n;
}
Map<Integer,Integer> men_result = new HashMap<>();
men_result.put(0, 0);
men_result.put(1, 1);
return fib_men(men_result, n);
}
private int fib_men(Map<Integer, Integer> men_result, int n) {
if(men_result.containsKey(n)) {
return men_result.get(n);
}
int result_n = fib_men(men_result,n-1) + fib_men(men_result,n-2);
men_result.put(n, result_n);
return result_n;
}
此思路比动态规划解法略好,主要是空间复杂度没有动态规划的高。
leetcode,第96题,Unique Binary Search Trees,
Given an integer
n, return the number of structurally unique BST's (binary search trees) which has exactlynnodes of unique values from1ton.Example 1:
Input: n = 3 Output: 5Example 2:
Input: n = 1 Output: 1Constraints:
1 <= n <= 19
这道题目需要思考的是,在只有俩个结点的情况下,无论俩个结点是什么值,它们是不是都是同样多的二叉搜索树个数?也就是虽然结点4,5和结点7,10它们都有着不同的值,但是4,5和7,10这俩种情况下,他们都只有俩种二叉搜索树,是不是说二叉搜索树的个数只与结点的个数有关,而与结点中的值无关?确实是的,二叉搜索树的个数只与结点个数有关。
一种根结点的情况是取决于左子树和右子树的情况,而左右子树的情况个数是由左右子树的结点个数决定的。左子树的情况个数与右子树的情况个数相乘得到了一种根结点的情况个数。并且根结点的值确定了,那么左右子树的结点个数也就确定了。
每种结点数量,我们都需要遍历所有的值作为根结点的情况,而根节点中值的变化,本质上其实就是左右子树的结点个数的变化,所以我们只需要从左子树结点个数为0遍历到左子树结点个数为总结点数量-1,还有一个结点是作为根节点的,因此需要-1。通过左右子树的结点个数相乘就可以得到。
按照上面的思路,我们可以使用递归来实现,每层递归都是为了实现结点数量为n的情况下二叉搜索树的个数,因此每层都需要进行遍历所有的值作为根节点,实际编程中是对左子树的结点个数进行遍历,范围就是[0, n-1]。不过普通的递归效果不好,时间复杂度和空间复杂度都很高,我们可以从简单的三个结点入手,来看一下整个过程。
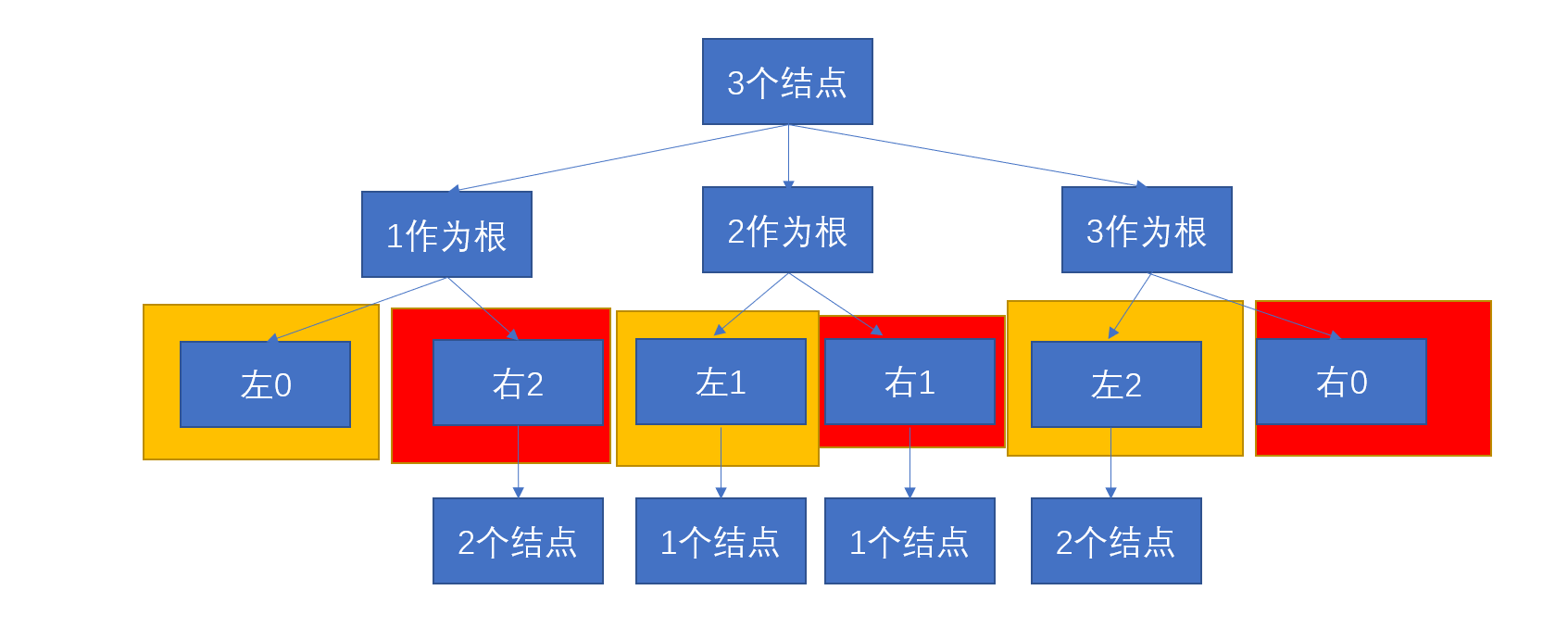
三个节点的话,遍历左子树的结点个数,
- 左子树结点个数为0(1作为根结点),右子树结点个数为2,之后统计结点个数为2的情况下,二叉搜索树的个数为多少。
- 左子树结点个数为1(2作为根结点),右子树结点个数为1,之后统计结点个数为1的情况下,二叉搜索树的个数为多少。
- 左子树结点个数为2(3作为根结点),右子树结点个数为0,之后统计结点个数为2的情况下,二叉搜索树的个数为多少。
从上面的过程中,我们可以看出里面是包含了大量重复的计算,因此使用了记忆化递归来做,使用map来记录结点数量与二叉搜索树数量的关系。
// 回溯判断
Map<Integer,Integer> num_map = new HashMap<>();
public int numTrees(int n) {
if(n == 1 || n == 0) {
return 1;
}
if(num_map.containsKey(n)) {
return num_map.get(n);
}
int num = 0;
for(int index = 0; index < n; ++index) {
num += numTrees(index)*numTrees(n-index-1);
}
num_map.put(n, num);
return num;
}
当然此题使用动态规划的思想来做是最好的,因为从上面我们看出结点数量为3的计算是用到了结点数量为2的计算,我们需要计算是结点个数为index的情况下,左子树的结点个数为num,num的范围为[0, index-1],因为还有一个点作为根节点。那么右子树就是结点个数就是index-num-1,之后将左右子树的个数乘机全部相加就是该结点数量下二叉搜索树个数。
// 动态规划
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
dp[1] = 1;
for(int index = 2; index <= n; ++index) {
for(int num = 0; num < index; ++num) {
dp[index] += dp[index - num - 1]*dp[num];
}
}
return dp[n];
}
链表问题
此章节是根据具体的链表问题来看递归法,虽然链表问题会在后续的leetcode -- 数据结构来介绍,但是递归法这边也留个印象,进行一下整理,链表的拷贝、合并、反转和交换,其中链表的反转笔试题中出现过,因而还是很重要的。链表是因为无法直接存取,只能遍历查找元素,因而很多时候都需要使用递归来对链表上的元素进行操作。我们在解决链表问题的时候,最好先在草稿纸上整理好思路再进行代码的实现。
下面先来一道简单的链表深拷贝问题。
leetcode, 第138,Copy List with Random Pointer,
A linked list of length
nis given such that each node contains an additional random pointer, which could point to any node in the list, ornull.Construct a deep copy of the list. The deep copy should consist of exactly
nbrand new nodes, where each new node has its value set to the value of its corresponding original node. Both thenextandrandompointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list.For example, if there are two nodes
XandYin the original list, whereX.random --> Y, then for the corresponding two nodesxandyin the copied list,x.random --> y.Return the head of the copied linked list.
The linked list is represented in the input/output as a list of
nnodes. Each node is represented as a pair of[val, random_index]where:
val: an integer representingNode.valrandom_index: the index of the node (range from0ton-1) that therandompointer points to, ornullif it does not point to any node.Your code will only be given the
headof the original linked list.Example 1:
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]] Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]Example 2:
Input: head = [[1,1],[2,1]] Output: [[1,1],[2,1]]Example 3:
Input: head = [[3,null],[3,0],[3,null]] Output: [[3,null],[3,0],[3,null]]Example 4:
Input: head = [] Output: [] Explanation: The given linked list is empty (null pointer), so return null.Constraints:
0 <= n <= 1000-10000 <= Node.val <= 10000Node.randomisnullor is pointing to some node in the linked list.
此题是对链表进行深拷贝,链表结点中还包含了一个随机结点,最大的难点就是这个随机结点,这是因为如果你使用遍历的话,会发现随机结点不是一个新的结点,它是后面未遍历到的结点,因此在拷贝遍历的时候,并不能简单的创建一个新的结点,不过这道题遍历解法其实也是能做的,思路是俩次遍历,先遍历一遍链表,并且再遍历的同时,不断地创建新的结点,之后再来一次遍历,遍历的同时,设置好每一个结点的next和random,,不过递归方法写法更加简洁,因为随机结点有可能是后面未遍历到的结点,因此我们需要map记录好每一个创建的新结点。
Map<Node,Node> node_map = new HashMap<>();
// 递归操作
public Node copyRandomList(Node head) {
if(head == null) {
return head;
}
if(node_map.containsKey(head)) {
return node_map.get(head);
}
Node new_node = new Node(head.val);
new_node.next = copyRandomList(head.next);
new_node.random = copyRandomList(head.random);
node_map.put(head, new_node);
return new_node;
}
对于链表的操作,还有交换操作。
leetcode,第24题, Swap Nodes in Pairs,
Given a linked list, swap every two adjacent nodes and return its head.
Example 1:
Input: head = [1,2,3,4] Output: [2,1,4,3]Example 2:
Input: head = [] Output: []Example 3:
Input: head = [1] Output: [1]Constraints:
- The number of nodes in the list is in the range
[0, 100].0 <= Node.val <= 100Follow up: Can you solve the problem without modifying the values in the list's nodes? (i.e., Only nodes themselves may be changed.)
此题目就是交换相邻结点,如果使用递归来解题的话,那么递归函数的作用就是交换相邻结点,递归的结束条件就是遍历到最后或者只有一个结点无法交换的时候。
// 递归操作
public ListNode swapPairs(ListNode head) {
if(head == null || head.next == null) {
return head;
}
// 交换操作
ListNode next_node = head.next;
head.next = swapPairs(next_node.next);
next_node.next = head;
return next_node;
}
递归的写法是非常简单的,但是第一次写的时候,我们常常只会想到用迭代的算法来解题,只要每次都进行相邻结点的交换即可,但是交换结点的时候,如果交换的是头结点,那么交换完成了之后原先的头结点就不再是头结点,也就是头结点的交换操作与其他的不同,如果不注意处理,就会交换之后,后面的结点都会消失,最好的处理办法就是在头结点之前再设置一个头指针。
// 迭代解法
public ListNode swapPairs_1(ListNode head) {
if(head == null || head.next == null) {
return head;
}
// 设置头指针
ListNode root_pre = new ListNode(-1,head);
ListNode dummey = root_pre;
// 交换操作
while(head != null && head.next != null) {
ListNode right = head.next;
dummey.next = right;
head.next = right.next;
right.next = head;
// 迭代中的下一轮操作
dummey = head;
head = head.next;
}
return root_pre.next;
}
链表合并
这种题目往往就是将俩条链表合并,如果使用常规的迭代拼接法的话,写起来较为复杂,递归写法很简洁。
leetcode, 第21题,Merge Two Sorted Lists,
Merge two sorted linked lists and return it as a sorted list. The list should be made by splicing together the nodes of the first two lists.
Example 1:
Input: l1 = [1,2,4], l2 = [1,3,4] Output: [1,1,2,3,4,4]Example 2:
Input: l1 = [], l2 = [] Output: []Example 3:
Input: l1 = [], l2 = [0] Output: [0]Constraints:
- The number of nodes in both lists is in the range
[0, 50].-100 <= Node.val <= 100- Both
l1andl2are sorted in non-decreasing order.
此题是将俩个有序链表合并成一个有序链表,这道题使用递归的思路来解答,递归的函数,就是比较俩个结点的值,将小的结点拿出来作为一个点,然后将剩下的链表再进行对比,结束条件就是其中的一条链表变成null了,那么剩下的就都是这条链表了。
// 递归
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1 == null) {
return l2;
}
if(l2 == null) {
return l1;
}
if(l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next,l2);
return l1;
}else {
l2.next = mergeTwoLists(l1,l2.next);
return l2;
}
}
链表反转
链表反转,就是将链表反过来,因为链表是无法根据位置来交换,因此在这类题目的面前,使用的就是递归来解。
leetcode,第206题,Reverse Linked List,
Given the
headof a singly linked list, reverse the list, and return the reversed list.Example 1:
Input: head = [1,2,3,4,5] Output: [5,4,3,2,1]Example 2:
Input: head = [1,2] Output: [2,1]Example 3:
Input: head = [] Output: []Constraints:
- The number of nodes in the list is the range
[0, 5000].-5000 <= Node.val <= 5000Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?
此题就是简单的将链表进行反转,但是递归函数内部的实现还是比较困难的,递归返回的就是反转之后的链表,也就是最后一个结点,而之后的结点交换的话,就是当前结点head一个人的独角戏,将后面的结点与当前结点进行。
// 递归反转
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) {
return head;
}
ListNode pre = reverseList(head.next);
head.next.next = head;
head.next = null;
return pre;
}
当然这道题更一般的只要使用迭代回溯法就可以进行链表反转了,这个时候就要一个头指针,这个头指针就是与链表的头结点进行交换,不用头指针的话,链表头结点的交换考虑就比较复杂了。
// 回溯反转
public ListNode reverseList_1(ListNode head) {
ListNode pre = null;
ListNode curr = head;
while(curr != null) {
ListNode temp = curr.next;
curr.next = pre;
pre = curr;
curr = temp;
}
return pre;
}
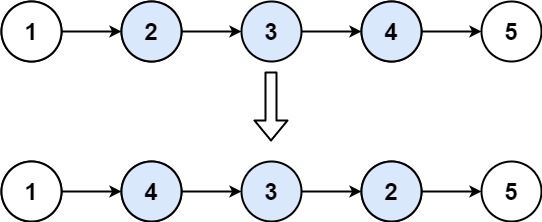
leetcode, 第92题,Reverse Linked List II,
Given the
headof a singly linked list and two integersleftandrightwhereleft <= right, reverse the nodes of the list from positionleftto positionright, and return the reversed list.Example 1:
Input: head = [1,2,3,4,5], left = 2, right = 4 Output: [1,4,3,2,5]Example 2:
Input: head = [5], left = 1, right = 1 Output: [5]Constraints:
- The number of nodes in the list is
n.1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= nFollow up: Could you do it in one pass?
此题是上一题的拓展,上一题是直接对整个链表进行反转,此题是对链表中部分结点进行反转,范围反转如果直接使用递归肯定不太好写,因为链表中的操作因为位置的变化而变化了,有的需要反转,有的不需要反转。我们现在重新定义一下题目,反转前n个结点,这样的话,就与之前的那道题差不多,差异就在于上一题最后是null,而反转前n个结点的话,最后是后面的那些不需要反转的结点。
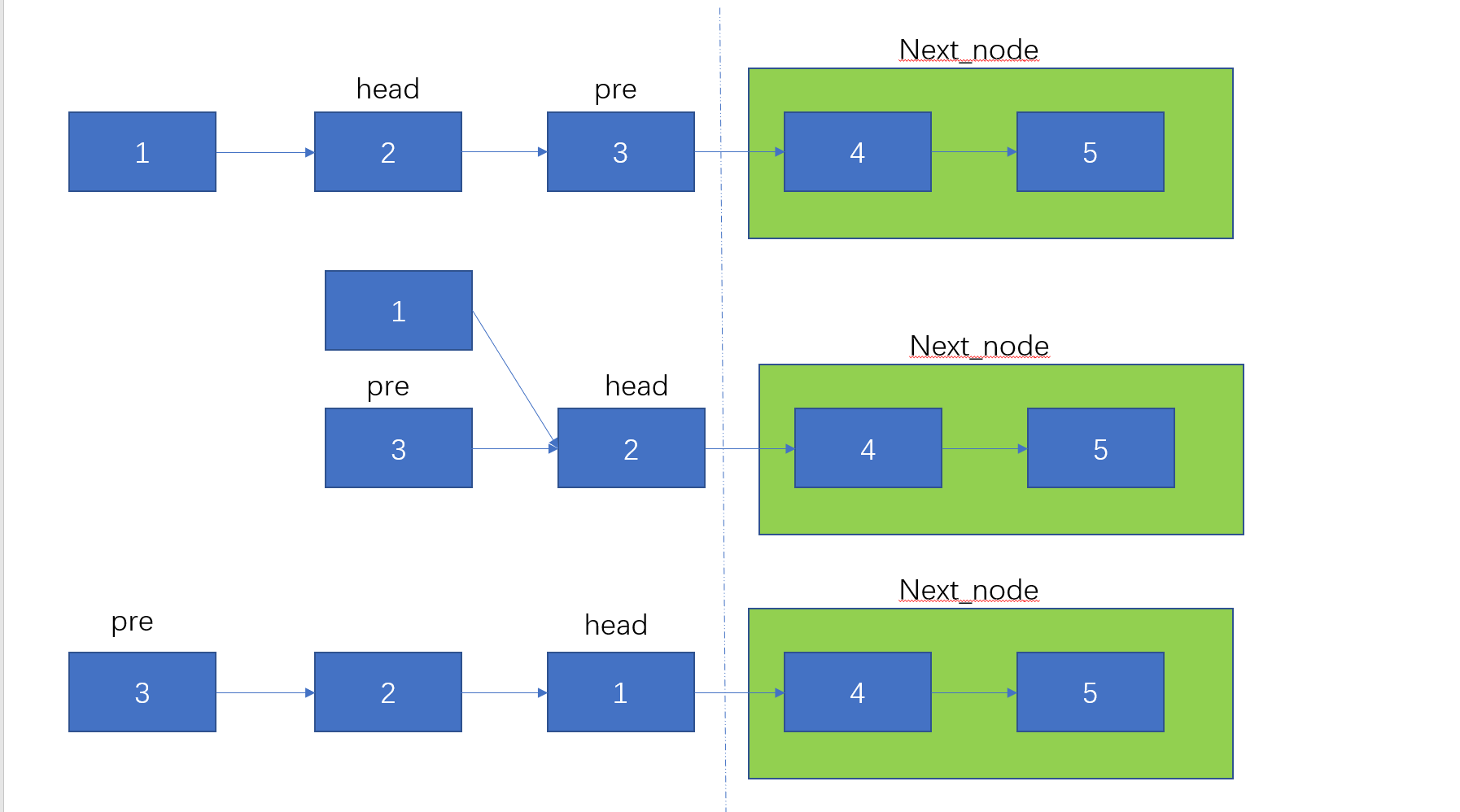
// 对前n个结点进行反转
ListNode next_node = null;
public ListNode reverseN(ListNode head, int right) {
if(right == 1) {
next_node = head.next;
return head;
}
ListNode pre = reverseN(head.next, right - 1);
head.next.next = head;
head.next = next_node;
return pre;
}
那么现在的问题是我们如何将范围内反转变成前N个结点反转了,那就是遍历到相应的位置上,最好的办法让m递减,一直递减到1的时候,这个时候就变成前N个结点反转问题了,因此我们还需要一次递归将之遍历。
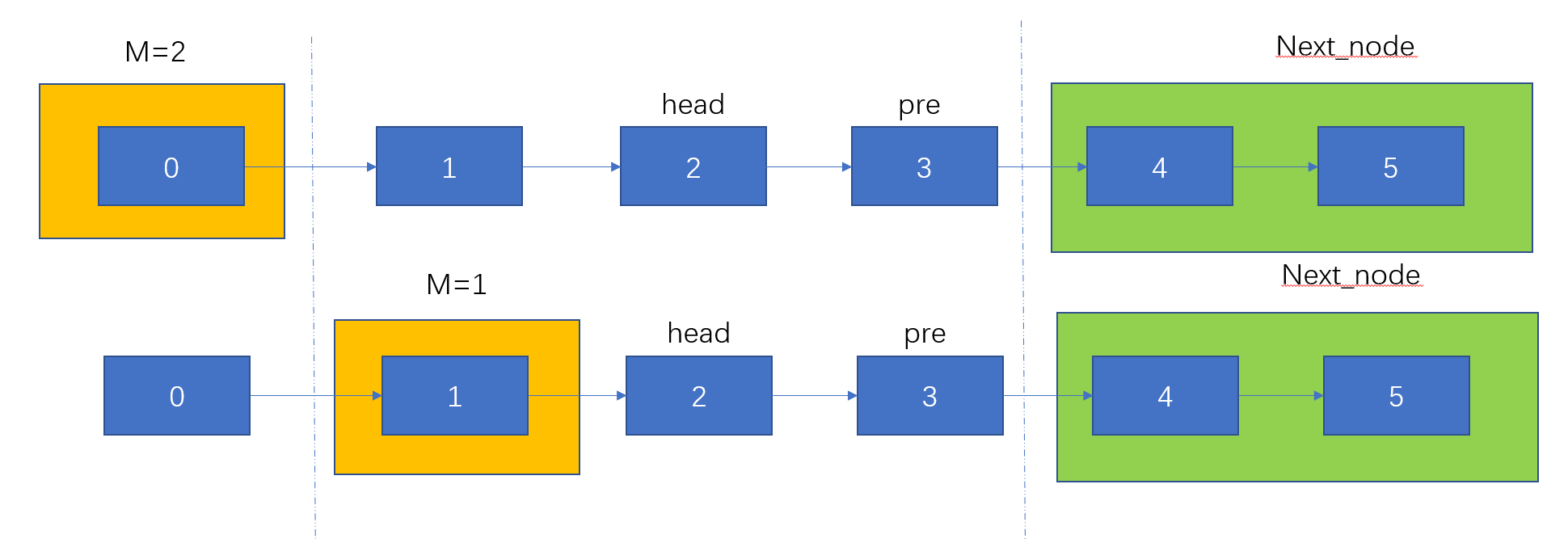
// 遍历反转
public ListNode reverseBetween(ListNode head, int left, int right) {
if(left == 1) {
return reverseN(head, right);
}
head.next = reverseBetween(head.next, left - 1, right - 1);
return head;
}
当然此题还可以使用上一题中的迭代解法来求解,只不过在大厂笔试的时候,你要在代码实现之前考虑完全清楚,因为没有提示那些数据不行,这样你可能想不到BUG出现在哪里。而使用迭代解法就需要考虑的很清楚,在范围反转,我们需要一直保存的有范围内的第一个结点,范围内的第一个结点反转到最后一个结点中去,还需要将范围外后部分结点与它相连,范围外的前部分的最后一个结点,它与需要与范围内的最后一个结点(反转过后就是第一个结点)相连,因此这俩个是需要保存下来的。并且在left为1的时候,就是变成反转前N个结点的问题的时候,还需要单独思考的,因此在left为1或者不为1的情况下,是有俩种返回值,这俩种我们都是需要考虑到的。
// 迭代求解
public ListNode reverseBetween_1(ListNode head, int left, int right) {
if(left == right) {
return head;
}
ListNode curr_node = head;
ListNode pre_node = null;
ListNode rever_pre_node = new ListNode();
// 它必须要初始化,这是为了防止Left=1的情况
ListNode rever_node = head;
for(int index = 1; index <= right; ++index) {
// 到了范围外前部分的最后一个点
if(index + 1 == left) {
// 需要进行记录
rever_node = curr_node.next;
if(left > 1) rever_pre_node = curr_node;
}
// 进入反转范围内了
if(index >= left) {
// 进行交换
ListNode temp = curr_node.next;
curr_node.next = pre_node;
pre_node = curr_node;
if(index == right) {
rever_node.next = temp;
if(left > 1) rever_pre_node.next = curr_node;
break;
}
curr_node = temp;
}
if(index < left) curr_node = curr_node.next;
}
if(left > 1) return head;
return curr_node;
}
约瑟夫环
约瑟夫环算是一个非常经典的问题,在很多笔试和算法面试中都会提及这个问题,
剑指offer,第62题,圆圈中最后剩下的数字,
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
输入: n = 5, m = 3 输出: 3示例 2:
输入: n = 10, m = 17 输出: 2限制:
1 <= n <= 10^51 <= m <= 10^6
此题是求最后存活下来的那个数字,假设n=5,m=3,那么每次都取第3个数删除,这个每次取数最大不同就是起始位置不同,步长都是一样的,假如我们一开始就知道了f(n,m)的那个存活的数字是x,因为数字是从0开始的,因此是从起始点数到x+1,这个数到x+1的位置就是存活数,这里的f(n,m)=x就表示n个数的时候,存活下来的数的索引是x,那么我们来看经过一轮m的删除会变成什么样子。
第一,删除的数应该就是(m-1)%n这个位置上的数,
第二,我们删除了一个数,那么在f(n-1,m)情况下存活的那个数是多少,我们假设f(n-1,m)=y,也就是存活下来的是y。
那么就是说第二次是从(m-1)%n数,数到y+1就是那个存活下来的数,而f(n,m)和f(n-1,m)这种存活下来的数应该都是一样的,因此
其中是利用取余操作进行化简的
这下就可以得到算法的递归式\(f(n,m) = [m + f(n-1,m)]\%n\),那么这个公式就是递归公式,那么还要考虑一个问题,递归结束条件是什么?递归到最后的时候应该是f(1,m),也就是只有一个数,这个数的索引一定是0,而这个0经过一系列的递归回溯,直到n的时候也就变成x。
// 递归操作
public int lastRemaining(int n, int m) {
if(n == 1) {
return 0;
}
return (lastRemaining(n-1, m) + m)%n;
}
我们还可以将这种递归操作变成迭代操作,我们想想最后一个数一定是0,那么这个0一直反推的话,就能得到这个数最开始的索引,这也就是靠着最终活的数进行反推即可。下面我利用狼人杀对n=5,m=3进行推导。

上面说最后一个数一定是0的意思就是最后一个数的位置一定在0这个位置,而我们的题目上位置就是这个数的值,因此最后一个数一定是0,不过我们看上面的推导,发现最后一个是小智,为了能快速找出狼人,我们最好在第一轮小刚被刀的时候,进行一次讨论,进行一次复盘,
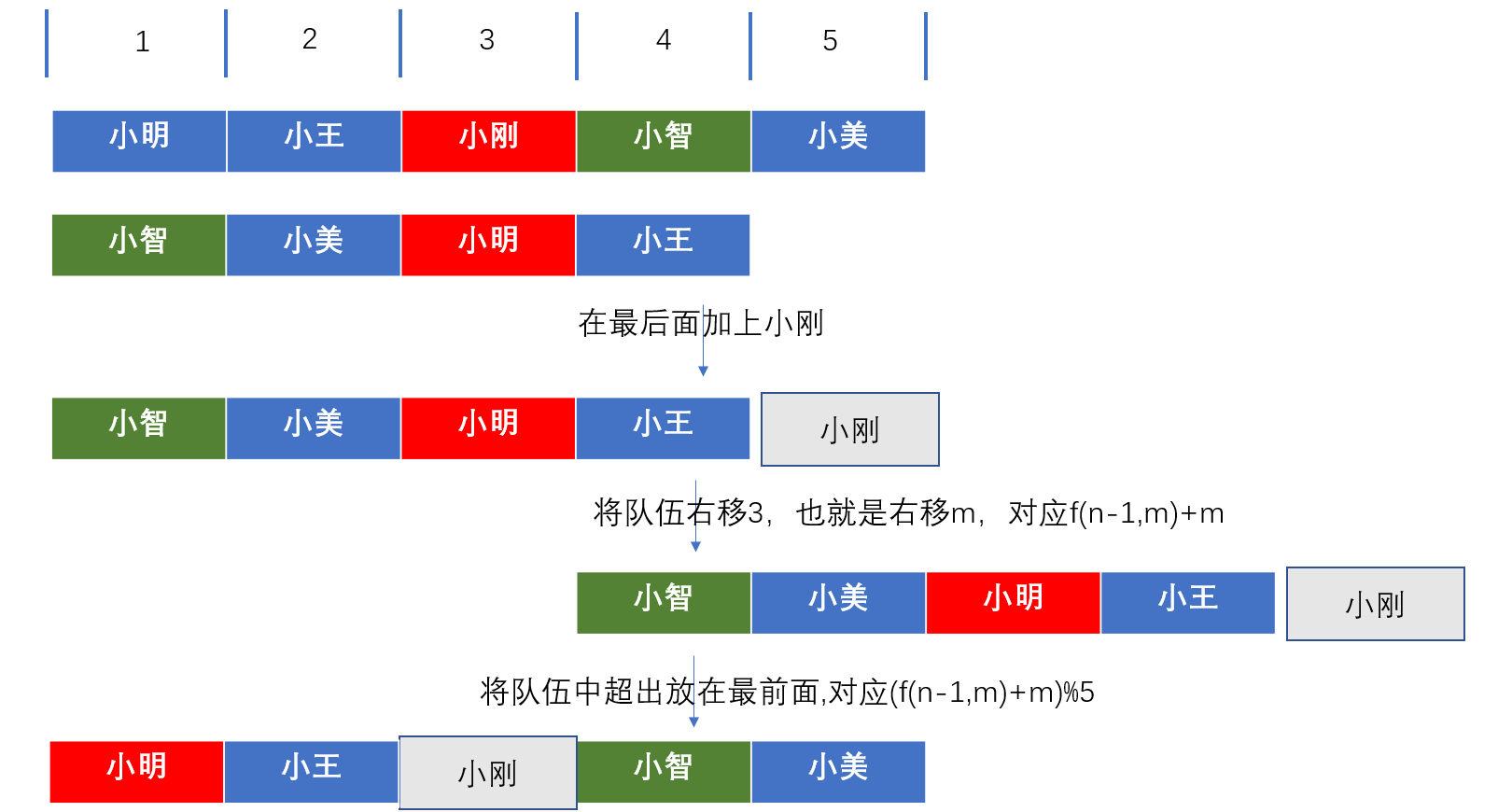
复盘我们发现,只要在队伍的最后加上小刚,之后右移m位,再将超出队伍的人离到最前面就是小刚没死之前的队伍了,这个超出队伍,就得看队伍在此时是有多长,上面是小刚被杀之前队伍是5,所以是对5进行取余,如果是最后只有狼人,想要恢复到俩个人的时候,队伍的长度就是2,所以最开始迭代应该是2,迭代到5即可,那么我们从最后一个存活的狼人位置进行迭代,最终得出的就是最开始狼人的位置。
// 迭代操作
public int lastRemaining_1(int n, int m) {
int live = 0;
for(int index = 2; index < n; ++index) {
live = (live + m)%index;
}
return live;
}
上述俩种算法都是能够通过的优秀思路,当然很多时候我们会使用暴力求解法,不过很遗憾的是,暴力求解并不能通过,会超时。这里说一下。首先想到的是使用链表来模拟这个约瑟夫环的过程,那么就需要将所有的数放入到链表中,之后我们进行遍历,因为从0开始的,因此只需要遍历到m-1的时候,就是要删除的那个数,那么最重要的是那些遍历的数如何操作呢?这里可以将遍历的数放到链表的最后面,那么链表的顺序在下一次遍历还是有效的。
// 链表操作
public int lastRemaining_2(int n, int m) {
List<Integer> last_list = new ArrayList<Integer>();
for(int temp = 0; temp < n; ++temp) {
last_list.add(temp);
}
while(last_list.size() > 1) {
for(int index = 0; index < m; ++index) {
if(index != m-1) {
last_list.add(last_list.get(0));
}
last_list.remove(0);
}
}
return last_list.get(0);
}
当然还可以使用其他的数据结构来做,可以使用双端队列,也可以使用数组等等,不过这些解决思路都不符合题目的时间限制。
总结
很多递归算法看起来很简单,只有几行代码,但是这些递归函数的过程往往很难被分析好,并且在很多时候,我在分析递归函数的时候都会被绕进去,因此递归算法的实现看起来简单,往往并不能轻易的被分析想到。本章也只是列举出一些比较典型的递归算法,要真正掌握这种递归算法,还是要进行刷题来融会贯通。