SVM,称为支持向量机,曾经一度是应用最广泛的模型,它有很好的数学基础和理论基础,但是它的数学基础却比以前讲过的那些学习模型复杂很多,我一直认为它是最难推导,比神经网络的BP算法还要难懂,要想完全懂这个算法,要有很深的数学基础和优化理论,本文也只是大概讨论一下。本文中所有的代码都在我的github。
硬间隔SVM推导
如果现在我们需要对一堆数据进行二分类处理,并且这些数据都是线性可分的(一条直线就能将数据区分开),那么你会如何对之进行划分?如图1。
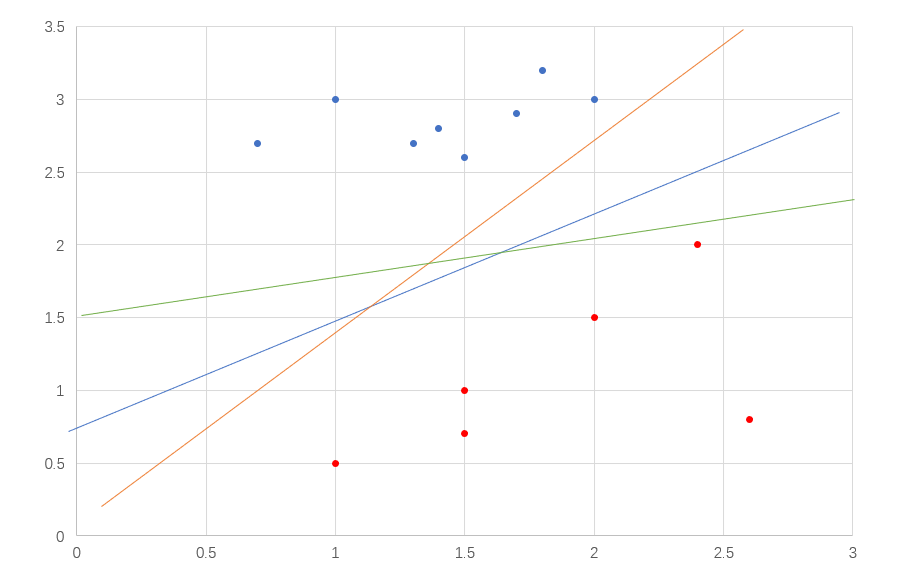
图1. 线性可分图
我们只需要在俩类数据的中间找出一条直线即可,如果数据是三维的,那么我们需要找出中间的切分面,能将俩类数据划分开的直线有很多,在图1中就有三条,那么你如何判断哪一条才是最适合的呢?直观来看,肯定是中间的蓝色线,因为黄线太靠近蓝点,绿线太靠近红色,这样的线对样本扰动的容忍性低,在测试集中很容易就会出错,而蓝色线是受影响最小的,因为它距离俩类样本最远,这样才具有泛化能力,那么我们需要找出的线就是距离俩类样本最远,其实就是最中间的线,从图1中可以看出平面上有很多点,问题在于哪些点才能衡量出线到俩类数据的距离呢?那肯定是距离线最近的那些点,我们把最近样本点到划分边界的距离称为间隔。我们的目标就是达到最大间隔的那个划分边界。下面先来求间隔。
间隔
用\(W^TX + b = 0\)来表示划分边界,我们先计算点到这个划分边界的距离,因为数据可能是高维的,所以不能用点到直线的距离,应该计算点到面的距离。图2就是计算其中有一个\(P\)到面的距离。
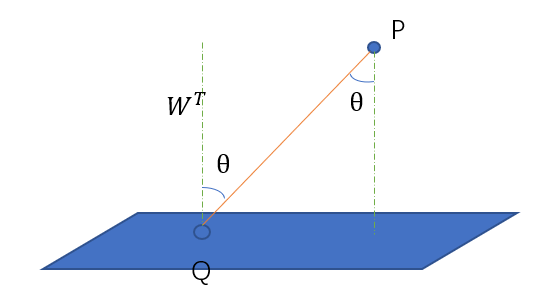
图2. 点到平面图
\(Q\)是平面上任意一点,其中\(W^T\)是平面的法向量,这个我们推导出来,假设平面上任意俩点\(x_1,x_2\),
\[W^T(x_1 - x_2) = W^Tx_1 - W^Tx_2 = (-b) - (-b) = 0
\]
因此\(W^T\)与平面垂直。设\(P\)到平面上距离为\(d\),从图中我们可以很容易的看出,
\[\begin{align}
d & = |PQ|cos\theta \notag \\
& = |P - Q|cos<W^T, P-Q> \notag \\
& = |P - Q| \frac{|W^T(P-Q)|}{|W||P - Q|} \notag \\
& = \frac{1}{|W|}|W^TP - W^TQ| \notag \\
\end{align}
\]
因为\(Q\)是平面上任意一点,所以\(W^TQ + b = 0\),点\(P\)到平面上的距离公式变成
\[d = \frac{1}{|W|}|W^TP + b|
\]
假设数据集\(D = \{(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\}\),点到划分边界的距离就是\(d = \frac{1}{|W|}|W^Tx_i + b|\),之前我们说最近样本点到划分边界的距离称为间隔,那么间隔用公式表示就是
\[margin = \min\limits_{i=1,2,\dots,n}(\frac{1}{|W|}|W^Tx_i + b|)
\]
这个公式也被称为几何间隔,是我们的目标。
因为\(\frac{1}{|W|}\)和\(min\)没有关系,可以直接提到前面去,
\[margin = \frac{1}{|W|}\min\limits_{i=1,2,\dots,n}(|W^Tx_i + b|)
\]
现在单独来看这个公式,我们可以将绝对值符号替换掉不?绝对值里面的数一定是正数,如果所有的数据都会正确分类,没有那种错误的数据,那么\(W^Tx_i + b\)在负类中的结果是负数,\(W^Tx_i + b\)在正类中的结果是正数,我们一般将负类表示为-1,正类表示为1,那么就有办法了,直接将之乘以各自的类别,
\[|W^Tx_i + b| = y_i(W^Tx_i + b)
\]
我们再来看看这个式子的含义,数据如果带入\(y_i(W^Tx_i + b)\),计算出来的肯定不是0,因为结果0代表这个点就在这个划分边界上,肯定是一个数,并且带入的点离划分边界越远,计算出来的结果就越大,我们就有更大的把握将之分类正确,那么\(y_i(W^Tx_i + b)\)其实就是数据分类的置信度,我们也将之称为函数间隔,这里的置信度不是概率而是一个确切的值,没有统一的量纲,会出现问题,我们如果将划分边界的\(W\)和\(b\)等比例放缩,比如将\(x + y + z + 1 = 0\)变成\(2x + 2y + 2z + 2 = 0\),这样放缩过后的平面与原来的平面其实还是同一个平面,平面没变,点的位置也没变,那么几何间隔不变,但是函数间隔就发生了变化,扩大2倍,那么我们就需要将划分边界的\(W\)和\(b\)的比例定下来,这个比例就是随便定哪种,因为它不影响几何间隔的大小,既然比例可以随便定了,那么我就定成最小点到平面距离为1的比例,也就是\(y_i(W^Tx_i + b) = 1\),那么间隔大小就是
\[margin = \frac{1}{|W|}
\]
我们的目标就是达到最大间隔的那个划分边界,别忘了还有条件,数据能够被完全正确划分,用公式表示就是,
\[\max\limits_{W,b}(margin) = \max\limits_{W,b}\frac{1}{|W|} \\
s.t. y_i(W^Tx_i + b) \geq 1
\]
对于函数间隔设置为1,除了之前的代数角度,还可以从另一个角度来看,平面的变化就是\(W\)和\(b\)的变化,我们需要找出最好的划分边界,那么就需要不断地变化\(W\)和\(b\)来表示不同的划分边界,\(W\)和\(b\)有俩种,一种是等比例,另一种是不等比例,等比例变化之后还是原来的平面,这明显不是我们想要的,我们想要的是不同的平面,那么就需要不等比例,那么我们就将函数间隔缩放成1,每次调整参数的时候,都会按比例把函数间隔缩放成1,这样变化\(W\)和\(b\)就不会出现第一种情况了。
现在这个问题就变成了求最大值的问题,在机器学习中就是优化问题,在优化最值问题中,一般都求最小值,因为如果你求最大值的话,你没有上界,你无法判断出结果如何,但是在求最小值中,我们可以将0当成下界,所以可以将之转化为最小值问题,就变成了\(\min\limits_{W,b}|W|\)。这里就需要比较向量的大小,专业化就是度量向量大小,在数学中可以使用范式,最常用的欧氏距离就是2范式,我们也将之变成2范式,并且为了简化之后的计算,在前面加上\(\frac{1}{2}\),就变成了
\[\min\limits_{W,b}\frac{1}{2}|W|^2 \\
s.t. y_i(W^Tx_i + b) \geq 1,i=1,2,\dots,n
\]
我们可以利用QP解法来直接求这个最小值,但是一旦要引入核函数,那么这种解法就很复杂了,没有效率,因此需要利用优化来求解。
对偶
上面的求最值问题在机器学习中被称为优化问题,从导数的时候,我们就学过求函数的最值,是利用导数为0,不过那时候是没有约束条件的,后来上大学,高数中出现求等式约束条件下多元函数的极值,这个时候我们来看怎么求,有了约束条件,那么取值就有范围,只能在这个等式中的值,我们可以通过图来直观的感受,这里我们使用的是等高线图来表示值的大小,并且用公式表示约束就是
\[minf(x) \\
s.t. h(x) = 0
\]
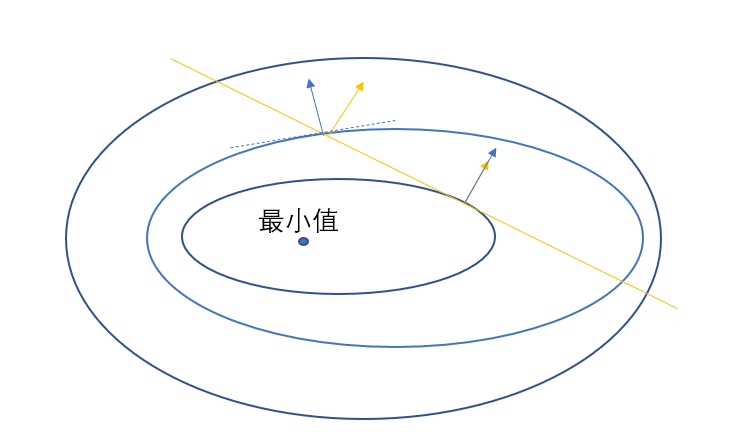
图3. 等式约束条件下的等高线图
图3中蓝色线就是值的等高线,是函数$f(x)$的值,黄线就是等式约束条件,等式约束条件就是$h(x)$,在约束条件下,值是先变小,小到一定程度之后开始慢慢变大,当黄线到达极小值的时候,必然会有等高线与之相切,在极值点处$x^{\ast}$,黄线的梯度与等高线垂直,而等高线自身的梯度也是与等高线垂直,那么黄线的梯度与等高线的梯度共线,自然就有了
$$
\bigtriangledown f(x^{\ast}) = \lambda \bigtriangledown h(x^{\ast})
$$
并且这个极值点处$x^{\ast}$在等式约束条件$h(x)$中也是存在的,因此也要满足
$$
h(x^{\ast}) = 0
$$
上面俩个等式就是求极值点所需要的俩个条件,有了它们就能求,为了能将它们都包含在无约束的优化问题中,就设计出了这样一个函数。
$$
L(x,\lambda) = f(x) + \lambda h(x) \\
s.t. \lambda \geq 0
$$
这个就是拉格朗日函数,一般拉格朗日函数都是需要对$x$和$\lambda$求偏导的,我们求出偏导就发现这俩个偏导和上面的俩个条件是一样的。
$$
\frac{\partial L}{\partial x} = \bigtriangledown f(x) + \lambda \bigtriangledown h(x) = 0 \\
\frac{\partial L}{\partial \lambda} = h(x) = 0
$$
但是在实际优化问题中很多都是不等式约束,如果只有一个不等式的话,那么还是使用拉格朗日即可。但是很多时候都有很多不等式,就比如我们上面的那个优化问题,它有\(n\)个不等式,这里我们先看有俩个不等式约束条件的情况,
\[min f(x) \\
s.t. h_1(x) \leqslant 0,h_2(x) \leqslant 0
\]
我们可以画出图形,就是
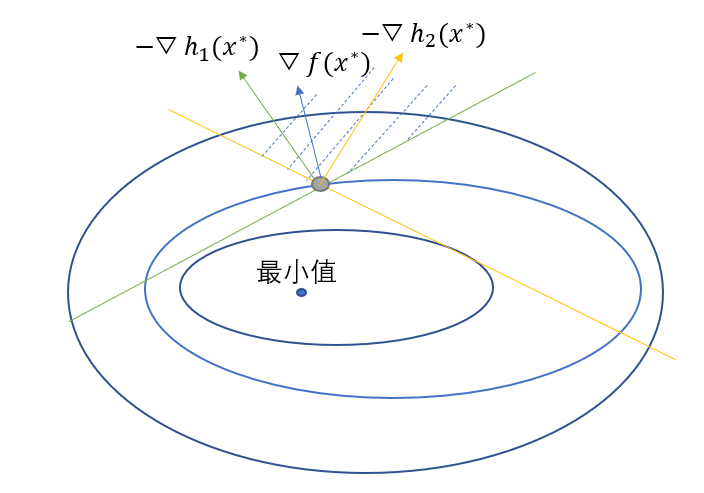
图4. 不等式约束条件下的等高线图
其中的黄线就是不等式约束$h_2(x)$,绿线就是$h_1(x)$,从图中可以看到函数$f(x)$在极值点处的梯度始终在俩条不等式约束梯度的中间,这在向量空间就是表示$\bigtriangledown f(x^{\ast})$可以由$-\bigtriangledown h_1(x^{\ast})$和$-\bigtriangledown h_2(x^{\ast})$线性表示出来,并且线性表示的系数必定是非负的,公式可以表示
$$
\bigtriangledown f(x^{\ast}) = -\mu_1\bigtriangledown h_1(x^{\ast})-\mu_2\bigtriangledown h_2(x^{\ast}) \\
\mu_1 \geq 0, \mu_2 \geq 0
$$
这个俩个分别是梯度为0条件和可行条件,当然,在约束条件中,还有一种情况,就是线性表示与其中一些不等式梯度无关,比如再加上一个不等式约束为$h_3(x)$,在图中表示就是
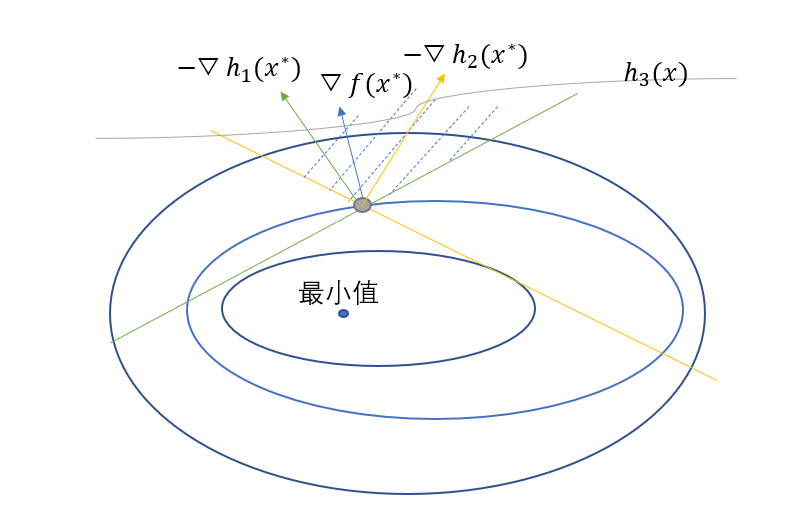
图5. 特殊情况下不等式约束条件下的等高线图
从图中可以看出灰线所表示的约束与线性表示无关,因为它的最小值不在\(x^{\ast}\),但是我们的条件还是要写成
\[\bigtriangledown f(x^{\ast}) = -\mu_1\bigtriangledown h_1(x^{\ast})-\mu_2\bigtriangledown h_2(x^{\ast})-\mu_3\bigtriangledown h_3(x^{\ast}) \\
\mu_1 \geq 0, \mu_2 \geq 0, \mu_3 \geq 0
\]
那么其中的\(\mu_3\bigtriangledown h_3(x^{\ast})\)该如何消去呢,那么再增加一个互补松弛条件就是
\[\mu_1h_1(x^{\ast})+\mu_2h_2(x^{\ast})+\mu_3 h_3(x^{\ast}) = 0
\]
因为在极值点处,\(h_1(x^{\ast})\)和\(h_2(x^{\ast})\)都是为0的,但是\(h_3(x^{\ast})\)不是0,用图中线段的话,\(h_3(x^{\ast}) < 0\),那么\(\mu_3 = 0\),这样就能弥补上面条件的缺陷了。这三个条件也被称为KKT条件,KKT条件就是存在局部极小值点的必要条件,整理起来就是
\[\mu_1 \geq 0, \mu_2 \geq 0, \mu_3 \geq 0 \\
\bigtriangledown f(x^{\ast}) + \mu_1\bigtriangledown h_1(x^{\ast})+\mu_2\bigtriangledown h_2(x^{\ast})+\mu_3\bigtriangledown h_3(x^{\ast}) =0 \\
\mu_1h_1(x^{\ast})+\mu_2h_2(x^{\ast})+\mu_3 h_3(x^{\ast}) = 0
\]
KKT条件是强对偶关系的充要条件,很多优化原问题很难求解,就需要找出原问题的对偶问题来求解。顺便说一下,slater条件是强对偶关系的充分非必要条件。而凸二次规划问题是一定满足slater条件,我们的SVM就是一个凸二次规划问题,因为它的目标函数\(f(x)\)是凸函数,并且约束都是放射函数,所以它一定是满足强对偶关系的,但是下面推导我们依旧慢慢推导。
上面无论什么约束,目标函数\(f(x)\)和约束函数\(h(x)\)都是变成一个式子的,因此我们先将之转变为拉格朗日函数,变成无约束问题。将约束条件转变为一般形式
\[1-y_i(W^Tx_i + b) \leq 0
\]
之后变成拉格朗日函数
\[L(x,\lambda) = \frac{1}{2}|W|^2 + \sum\limits_{i=1}^{n}\lambda_i(1-y_i(W^Tx_i + b)) \\
s.t. \lambda_i \geq 0
\]
那么我们能不能用拉格朗日函数来表示原问题呢?当然也是可以的,原问题是优化问题,可以转变为极大极小问题,
\[\min\limits_{W,b}\frac{1}{2}|W|^2 = \min\limits_{W,b}\max\limits_{\lambda}L(x,\lambda)
\]
我们可以分情况来讨论,当\(1-y_i(W^Tx_i + b) > 0\)的时候,\(L(x,\lambda)\)没有最大值,或者说最大值是\(+\infty\),当\(1-y_i(W^Tx_i + b) \leq 0\)的时候,\(L(x,\lambda)\)有最大值,最大值就是\(\frac{1}{2}|W|^2\),那么上面的极小极大可以变成
\[\min\limits_{W,b}\max\limits_{\lambda}L(x,\lambda) = \min\limits_{W,b}(+\infty, \frac{1}{2}|W|^2) = \min\limits_{W,b}\frac{1}{2}|W|^2
\]
其中\(\lambda_i\)用于表达约束,上式中\(\max\limits_{\lambda}L(x,\lambda)\)无法求,更无法使用偏导来求,因为式子\(L(x,\lambda)\)中的\(W\)和\(b\)没有固定住。那么这样不行的话,就使用对偶问题来求,一般式都是满足弱对偶关系的,也就是
\[\min\limits_{W,b}\max\limits_{\lambda}L(x,\lambda) \leq \max\limits_{\lambda}\min\limits_{W,b}L(x,\lambda)
\]
弱对偶关系很简单,但是我们想要的是强对偶关系,那么就需要用到上面所说的KKT条件,那么我们求解KKT条件,先来看自带的约束条件和KKT乘子条件就是
\[1-y_i(W^Tx_i + b) \leq 0 \\
\lambda_i \geq 0
\]
第二个条件就是梯度为0条件,那么需要对\(W\)和\(b\)进行求导
\[\frac{\partial L}{\partial W} = W - \sum\limits_{i=1}^{n}\lambda_iy_ix_i = 0 \\
\frac{\partial L}{\partial b} = \sum\limits_{i=1}^{n}\lambda_iy_i = 0
\]
第三个条件就是互补松弛条件,对于任意的i,都有
\[\lambda_i(1-y_i(W^Tx_i + b)) = 0
\]
满足了这三条要求,我们就可以转化为对偶问题了,得到了
\[\max\limits_{\lambda}\min\limits_{W,b}L(x,\lambda)
\]
那么先对其中的\(W\)和\(b\)求偏导,其中也就是KKT中的第二个条件,
\[\frac{\partial L}{\partial W} = W - \sum\limits_{i=1}^{n}\lambda_iy_ix_i = 0 \\
\frac{\partial L}{\partial b} = \sum\limits_{i=1}^{n}\lambda_iy_i = 0
\]
那么可以得到
\[W = \sum\limits_{i=1}^{n}\lambda_iy_ix_i \\
\sum\limits_{i=1}^{n}\lambda_iy_i = 0
\]
将之带入到原方程中去,
\[\begin{align}
L(x,\lambda) & = \frac{1}{2}W^TW + \sum\limits_{i=1}^{n}\lambda_i(1-y_i(W^Tx_i + b)) \notag \\
& = \frac{1}{2}\sum\limits_{i=1}^{n}\lambda_iy_ix_i^T\sum\limits_{j=1}^{n}\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i-\sum\limits_{i=1}^{n}\lambda_iy_iW^Tx_i -\sum\limits_{i=1}^{n}\lambda_iy_i b \notag \\
& = \frac{1}{2}\sum\limits_{i=1}^{n}\lambda_iy_ix_i^T\sum\limits_{j=1}^{n}\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i-\sum\limits_{i=1}^{n}\lambda_iy_i(\sum\limits_{j=1}^{n}\lambda_jy_jx_j^T)x_i -\sum\limits_{i=1}^{n}\lambda_iy_i b \notag \\
& = -\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i \notag \\
\end{align}
\]
那么我们可以求得
\[\min\limits_{W,b}L(x,\lambda) = -\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i \notag
\]
最终的式子就是
\[\max\limits_{\lambda}\min\limits_{W,b}L(x,\lambda) = \max\limits_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i \notag \\
s.t. \lambda_i \geq 0,\sum\limits_{i=1}^{n}\lambda_iy_i = 0 \\
\]
划分边界中的\(W^{\ast} = \sum\limits_{i=1}^{n}\lambda_iy_ix_i\),而我们假设最近样本点就是\((x_k,y_k)\),还可以求出\(b^{\ast} = y_k - \sum\limits_{i=1}^{n}\lambda_iy_ix_i^Tx_k\)。
超平面就是\(f(x) = sign(W^{T\ast}x+b^{\ast})\),还缺少的KKT条件就是
\[\lambda_i \geq 0 \\
1-y_i(W^Tx_i + b) \leq 0 \\
\lambda_i(1-y_i(W^Tx_i + b)) = 0
\]
此时会过来看SVM,叫做支持向量机,其中的支持向量,其实就是最近样本点,为什么这样说呢?我们看第四个条件,也就是\(\lambda_i(1-y_i(W^Tx_i + b)) = 0\),只有当\(y_i(W^Tx_i + b) = 1\)的时候,\(\lambda_i\)才不会为0,如果\(y_i(W^Tx_i + b) > 1\),那么\(\lambda_i\)为0,\(\lambda_i\)为0的话就对超平面起不到任何的作用,你可以看\(W\)和\(b\)的解。所以SVM关注的只有那些最近样本点,如下图6中过虚线的那三个点就是支持向量,这也是和逻辑回归最大的不同,逻辑回归关注的是所有的样本点。那么问题来了,支持向量多还是少的时候,比较好呢?支持向量越多,训练得到的模型越复杂,就会有过拟合的风险,但是这也不是绝对的。
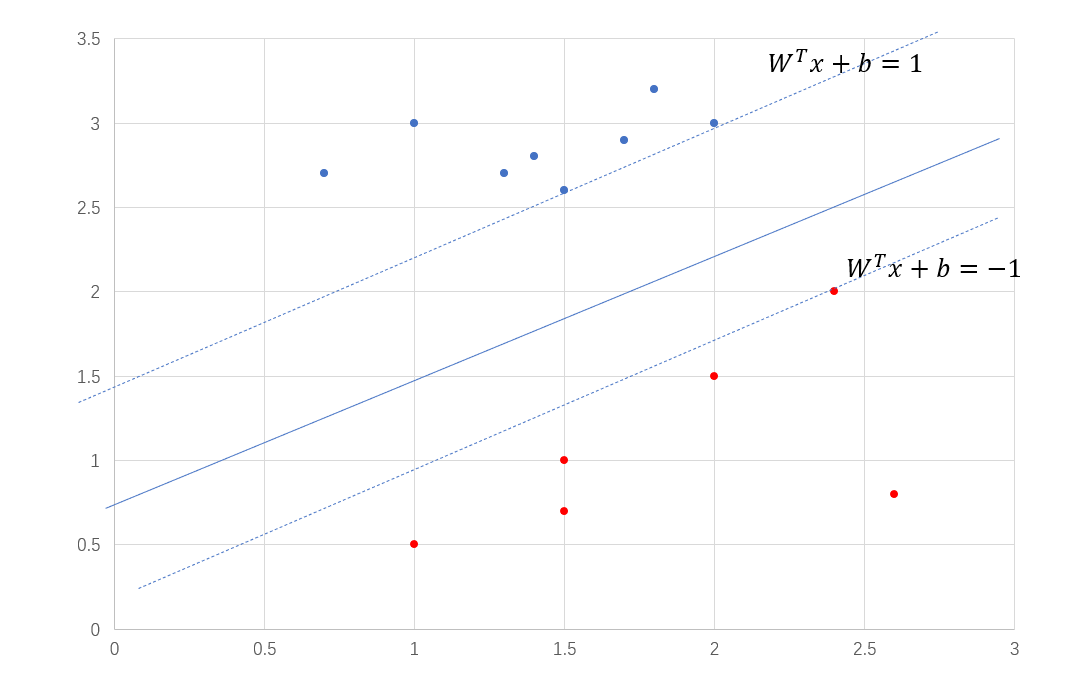
图6. SVM支持向量
SMO
对于上面的那个最终式子的求解,这种极值问题,之前逻辑回归中使用的梯度下降法,但是这种要求的是多个值,使用的就是坐标下降,每次沿着坐标的方向更新一次,就是每个值依次更新,比如在我们这个问题中,我们要更新\(\lambda_1\)的话,我们就需要固定其他的\(\lambda_i\)的值,然后求导进行更新,但是不能忘了我们的问题是有约束条件的,其中\(\sum\limits_{i=1}^{n}\lambda_iy_i = 0\)就说明如果固定其他的话,\(\lambda_1\)就完全等于一个固定的值了,\(\lambda_1 = -\sum\limits_{i=2}^{n}\lambda_iy_i\),不可能再更新啥的。每次更新一个值行不通的话,我们就每次固定住其他值,然后更新俩个值\(\lambda_1\)和\(\lambda_2\),这样的话,就不会出现上面的情况了,这就是序列最小优化算法SMO的基本思想,其中最小就是最小有俩个。
那么如何更新这俩个值呢?先来看如何更新最开始的\(\lambda_1\)和\(\lambda_2\),我们拿出最终式,将这个求最大值的式子先转化为最小值。
\[\max\limits_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i = \min\limits_{\lambda}\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j - \sum\limits_{i=1}^{n}\lambda_i
\]
我们设置方程\(K(\lambda_1,\lambda_2) = \frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j - \sum\limits_{i=1}^{n}\lambda_i\),然后将这个分解开,其实就是将关于\(\lambda_1\)和\(\lambda_2\)的式子提取出来,因为只有他们俩是未知的,其他都被固定了,可以看成实数。
\[\begin{align}
K(\lambda_1,\lambda_2) & = \frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j - \sum\limits_{i=1}^{n}\lambda_i \notag \\
& = \frac{1}{2}\lambda_1y_1x_1^T\lambda_1y_1x_1+ \lambda_1y_1x_1^T\lambda_2y_2x_2 + \frac{1}{2}\lambda_2y_2x_2^T\lambda_2y_2x_2 - (\lambda_1 + \lambda_2)+\lambda_1y_1\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_1 + \lambda_2y_2\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_2 + C \notag \\
\end{align}
\]
式子中的C就是代表了\(\sum\limits_{i=3}^{n}\lambda_i\),其中\(y_i\)就是标签,只有1和-1这俩种值,所以\(y_i^2 = 1\),我们将俩个\(x_i\)和\(x_j\)相乘标记为\(k_{ij}\),并且\(v_1 = \sum\limits_{i=3}^{n}\lambda_iy_ix_1x_i, v_2 = \sum\limits_{i=3}^{n}\lambda_iy_ix_2x_i\),那么上面的式子就可以化简成
\[\begin{align}
K(\lambda_1,\lambda_2) & = \frac{1}{2}\lambda_1y_1x_1^T\lambda_1y_1x_1+ \lambda_1y_1x_1^T\lambda_2y_2x_2 + \frac{1}{2}\lambda_2y_2x_2^T\lambda_2y_2x_2 - (\lambda_1 + \lambda_2)+\lambda_1y_1\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_1 + \lambda_2y_2\sum\limits_{i=3}^{n}\lambda_iy_ix_ix_2 + C \notag \\
& = \frac{1}{2}\lambda_1^2k_{11}+ \lambda_1\lambda_2y_1y_2k_{12} + \frac{1}{2}\lambda_2^2k_{22} - (\lambda_1 + \lambda_2)+\lambda_1y_1v_1 + \lambda_2y_2v_2 + C \notag \\
\end{align}
\]
因为\(\sum\limits_{i=1}^{n}\lambda_iy_i = 0\),除了\(\lambda_1\)和\(\lambda_2\),其他的都是固定的,那么\(\lambda_1y_1 + \lambda_2y_2 = \delta\),所以可以表示\(\lambda_1 = y_1(\delta- \lambda_2y_2)\),因此可以带入式中,式子现在只有一个变量\(\lambda_2\),
\[K(\lambda_2) = \frac{1}{2}(\delta- \lambda_2y_2)^2k_{11}+ (\delta- \lambda_2y_2)\lambda_2y_2k_{12} + \frac{1}{2}\lambda_2^2k_{22} - ( y_1(\delta- \lambda_2y_2) + \lambda_2)+(\delta- \lambda_2y_2)v_1 + \lambda_2y_2v_2 + C
\]
可以对\(\lambda\)进行求导,这个求导化简可以在纸上写一下,式子很多很长,我怕打错了,直接写出化简的最终式子。
\[\frac{\partial K}{\partial \lambda_2} = 0 得到\\
(k_{11} + k_{22} - 2k_{12})\lambda_2 = y_2(y_2 - y_1 + \delta k_{11} - \delta k_{12} + v_1 - v_2)
\]
并且其中的\(\delta = \lambda_1^{old}y_1 + \lambda_2^{old}y_2\),带入其中进行化简,为了区分开,将式子左边的\(\lambda_2\)变成\(\lambda_2^{new}\),设置其中的\(g(x) = \sum\limits_{i=1}^{n}\lambda_iy_ik(x_i,x)+b\),这个\(g(x)\)就代表了预测结果,从上面的\(W\)的求解式可以看出\(g(x) = W^Tx+b\),我们可以使用\(g(x)\)来替换式子中的\(v_i\),那么\(v_1 = g(x_1) - y_1\lambda_1k_{11} - y_2\lambda_2k_{12}-b\),最终式子化简变成了
\[\lambda_2^{new} = \lambda_2^{old} + \frac{y_2((g(x_1) - y_1) - (g(x_2) - y_2))}{k_{11} + k_{22} - 2k_{12}}
\]
在这个式中,我们需要考虑俩个范围,第一个就是\(\lambda_i\)的可行域,第二个就是\(k_{11} + k_{22} - 2k_{12}\)的大小。
之前我们提过\(\lambda_1y_1 + \lambda_2y_2 = \delta\),并且\(\lambda_1\)是一个实数,本身就是有范围的,我们设置为\(0 \leq \lambda_i \leq C\),并且\(\lambda_i\)也是需要满足\(\lambda_1y_1 + \lambda_2y_2 = \delta\),当\(y_1 = y_2\),那么\(\lambda_1 + \lambda_2 = \delta\),这边是1还是-1都是没有影响,当\(y_1 \ne y_2\),那么\(\lambda_1 - \lambda_2 = \delta\),我们画出这俩个式子的图像,如下图7所示。
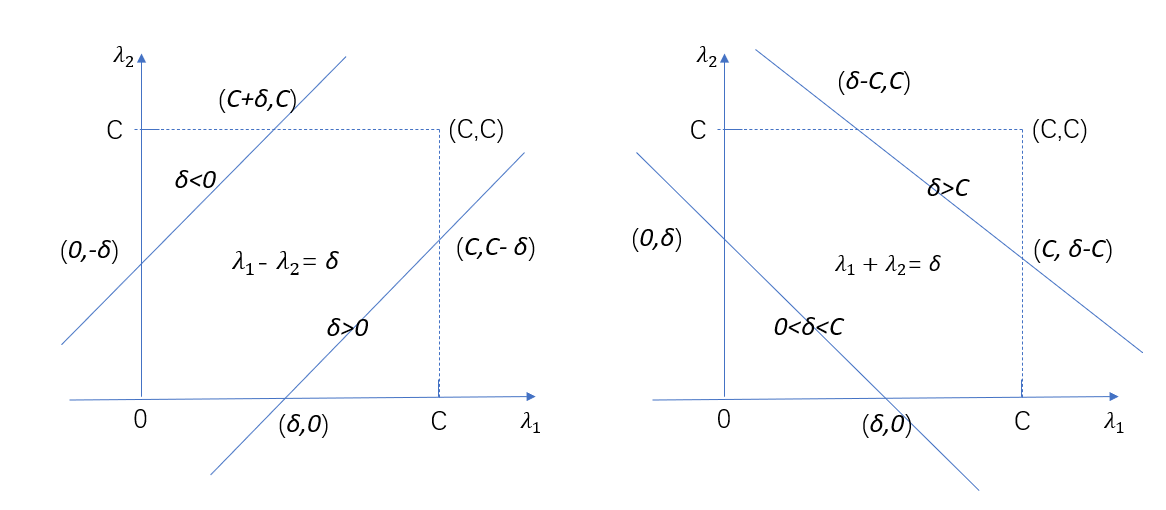
图7. 可行域范围
在左图中,也就是当\(y_1 \ne y_2\),\(\lambda_1 - \lambda_2 = \delta\)的时候,可以看到有俩种情况,第一种情况就是\(\delta < 0\),这时\(\delta_2 \in [-\delta,C]\),第二种情况就是\(\delta > 0\),这时\(\delta_2 \in [0,C-\delta]\),那么最小值\(low = max(0,-\delta)\),最大值\(high = min(C,C-\delta)\)。在右图中,当\(y_1 = y_2\),\(\lambda_1 + \lambda_2 = \delta\)的时候,也是俩种情况,第一种情况就是\(\delta > C\),这时\(\delta_2 \in [\delta - C,C]\),第二种情况就是\(0 < \delta < C\),这时\(\delta_2 \in [0,\delta]\),最小值\(low = max(0,\delta)\),最大值\(high = min(C,\delta-C)\)。所以\(low\)和\(high\)是分俩种情况的,这里我们统一用\(low\)和\(high\)表示,在代码中比较\(y_1\)和\(y-2\)即可,这就是它的定义域,因此
\[\lambda_2^{new} =
\begin{cases}
hight & \lambda_2^{new} > high,\\
\lambda_2^{new} & low \leq \lambda_2^{new} \leq high,\\
low & \lambda_2^{new} < low,\\
\end{cases}
\]
之后我们还需要考虑\(k_{11}+k_{22}-2k_{12}\)的取值范围,当它\(k_{11}+k_{22}-2k_{12} > 0\),那么最小值就在可行域中取到,但是如果\(k_{11}+k_{22}-2k_{12} \leq 0\),那么最小值就在边界\(low\)和\(high\)处取到了。
此时\(\lambda_2\)就被计算出来了,下面就是计算\(\lambda_1\),还是通过约束条件\(\lambda_1^{old}y_1 + \lambda_2^{old}y_2 = \lambda_1^{new}y_1 + \lambda_2^{new}y_2\)进行计算,下面就是推导过程。
\[\begin{align}
\lambda_1^{new}y_1 + \lambda_2^{new}y_2 & = \lambda_1^{old}y_1 + \lambda_2^{old}y_2 \notag \\
\lambda_1^{new}y_1 & = \lambda_1^{old}y_1 + \lambda_2^{old}y_2 - \lambda_2^{new}y_2 \notag \\
\lambda_1^{new} & = \lambda_1^{old} + (\lambda_2^{old} - \lambda_2^{new})y_1y_2 \notag \\
\end{align}
\]
在式子\(g(x) = \sum\limits_{i=1}^{n}\lambda_iy_ik(x_i,x)+b\)中也出现了b,那么我们还可以更新b,因为SMO的本质就是不断地移动划分边界来看谁最好,所以也是需要更新b的。
\[\begin{align}
b_1^{new} & = y_1 - W^Tx_1 \notag \\
& = y_1 - \sum\limits_{i=1}^{n}\lambda_iy_ik_{i1} \notag \\
& = y_1 - \lambda_1^{new}y_1k_{11} - \lambda_2^{new}y_2k_{21} - \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1} \notag \\
\end{align}
\]
我们需要化简上式中的\(y_1 - \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1}\),我们来看预测差值,也就是
\[\begin{align}
E_1 & = g(x_1) - y_1 \notag \\
& = \sum\limits_{i=1}^{n}\lambda_iy_ik(x_i,x_1)+b^{old} - y_1 \notag \\
& = \lambda_1^{old}y_1k_{11} + \lambda_2^{old}y_2k_{21} + \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1} - y_1 +b^{old} \notag \\
\end{align}
\]
从上式中可以得知\(y_1 - \sum\limits_{i=3}^{n}\lambda_iy_ik_{i1} = -E_1 + \lambda_1^{old}y_1k_{11} + \lambda_2^{old}y_2k_{21} +b^{old}\),因此b中的更新可以进行替换。
\[\begin{align}
b_1^{new} & = -E_1 + \lambda_1^{old}y_1k_{11} + \lambda_2^{old}y_2k_{21} +b^{old} - \lambda_1^{new}y_1k_{11} - \lambda_2^{new}y_2k_{21} \notag \\
& = -E_1 - y_1k_{11}(\lambda_1^{new} - \lambda_1^{old}) + y_2k_{21}(\lambda_2^{new} - \lambda_2^{old}) +b^{old} \notag \\
\end{align}
\]
那么所有解的推导式子都有了,更新只要根据式子进行更新就行。
上面的式子就能更新,选出俩个\(\lambda_i\),之后根据公式求得\(\lambda_i\),然后进行可行域的判断,是否超出了上下界,之后更新b。之后在初始选取俩个\(\lambda_i\)方面出现了很多方法,第一个\(\lambda_i\)大多数都是利用KKT条件,也就是选取不满足KKT条件,那为什么要选择呢?这是因为SMO其实就是调整划分边界的过程,其中肯定有不满足\(y_i(W^Tx_i+b) \geq 1\)的存在,如果一个\(\lambda_i\)违背KKT条件程度越大,它就表现得越靠近划分边界,最开始的最大值就会越小,它对最开始的最大化函数的减幅也是最大的,所以要先优化它。在代码中
# 检查是否满足KKT条件
if ((labelMat[i]*error < -toler) and (alphas[i] < C)) \
or ((labelMat[i]*error > toler) and (alphas[i] > 0)):
其中labelMat[i]就是数据类别,error就是误差,表现得就是\(error = W^Tx_i + b - y_i\),toler就是自己设置的容错率,alphas[i]就是\(\lambda_i\),先看第一个条件,其中的labelMat[i]*error < -toler表明了
\[y_i(W^Tx_i + b - y_i) < -toler \\
y_i(W^Tx_i + b) - 1 + toler < 0 \\
那么可得y_i(W^Tx_i + b)<1
\]
其中如果有软间隔的话,下面会讲,\(y_i(W^Tx_i + b)<1\)的数据都会被调整到支持向量上,这时\(\lambda_i = C\),但是\(\lambda_i < C\),这样的数据就不满足KKT条件了。第二个条件就是labelMat[i]*error > toler,那么
\[y_i(W^Tx_i + b - y_i) > toler \\
y_i(W^Tx_i + b) - 1 - toler > 0 \\
那么可得y_i(W^Tx_i + b)>1
\]
\(y_i(W^Tx_i + b)>1\)代表了它不是支持向量,是那些比较远的数据,这类数据如果想要满足KKT条件的话,\(\lambda_i = 0\),但是条件是\(\lambda_i > 0\),那么自然不满足KKT条件了。
对于第二个\(\lambda_i\)的选择,也有很多种方法,其中代表的就是选取与第一个差异最大的数据,能使目标函数有足够大的变化。
那么整理一下整个过程:
- 先选取一个\(\lambda_i\),计算它的误差,查看是否满足KKT条件(是否被优化);
- 满足条件,使用方法选择另外一个\(\lambda_j\),再计算它的误差;
- 约束\(\lambda_i\)和\(\lambda_j\)的可行域范围;
- 下面就是求新的\(\lambda_i\)的值了,根据是\(\lambda_i\)新和旧的公式,先计算那个分母,查看它的值;
- 根据公式计算出新的值,优化幅度不大的话,可以结束,进行下一轮;
- 计算出另外一个aj的新值;
- 计算出b的值;
- 如果已经没有被优化的次数超过了限制次数,说明不用优化了;
软间隔SVM
到目前为止,我们的SVM还很脆弱,它只能被用在线性可分的数据,并且还不能有噪声点,这样的模型是无法使用到现实数据中,因为现实数据的复杂性,会出现很多噪声点和离群点,
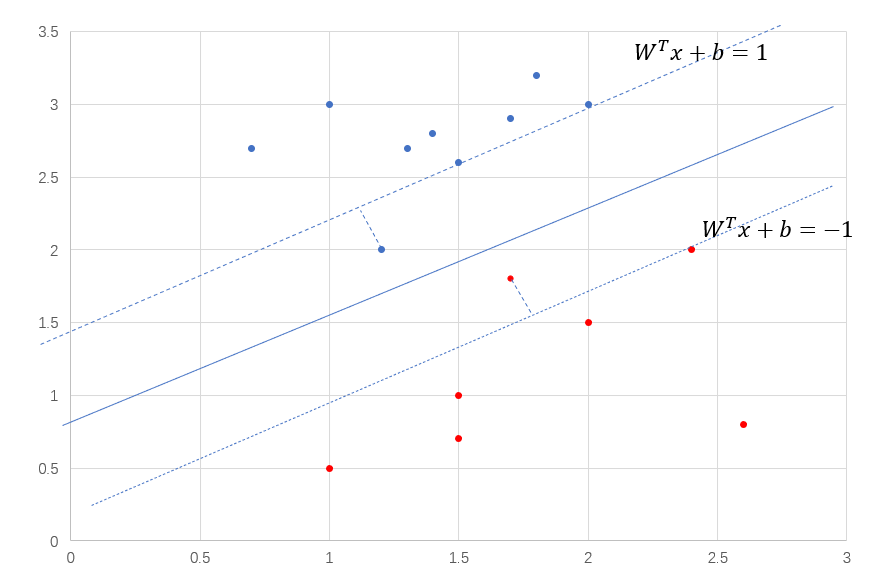
图8. 有噪声点的情况
从图8中看出,SVM的要求很严格,即使你分类正确了,也要达到一定的置信度,小于这个置信度,你依然会有损失的存在。我们需要处理这些在虚线内部的点,也就是让SVM放宽条件,允许模型犯一点小错误,让目标函数加上损失。
\[min\frac{1}{2}|W|^2 + loss
\]
关键是什么样的损失函数能够满足SVM?SVM模型只是由支持向量点决定的,对于普通的点,那是没有任何关系的,所以损失函数也要考虑到这一点,我们可以先来列出要求
- 如果\(y_i(W^Tx_i + b) \geq 1\),\(loss = 0\)。
- 如果\(y_i(W^Tx_i + b) < 1\),\(loss = 1 - y_i(W^Tx_i + b)\)
这样的话,我们将之组合起来,变成
\[loss = max\{0, 1-y_i(W^Tx_i + b)\}
\]
这样就能保持SVM解的稀疏性,我们将之称为hingle loss,合页损失。简单画一下它的图像就是
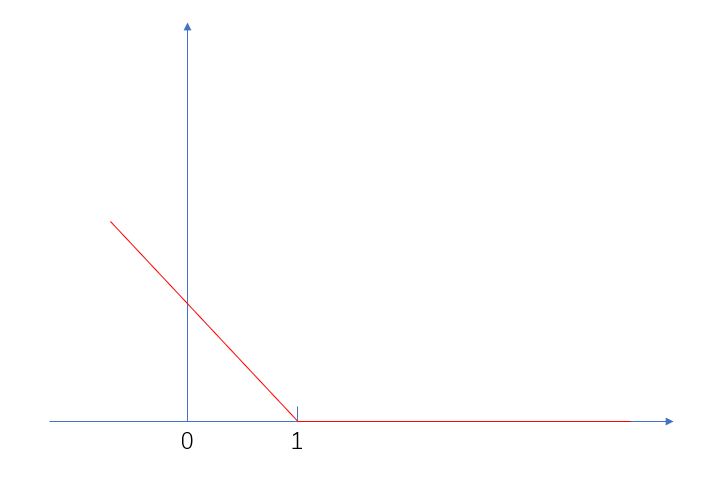
图9. hingle loss
这样我们就可以将损失带入到目标函数中,变成
$$
\min\limits_{W,b}\frac{1}{2}|W|^2 + C\sum\limits_{i=1}^nmax\{0, 1-y_i(W^Tx_i + b)\} \\
s.t. y_i(W^Tx_i + b) \geq 1,i=1,2,\dots,n
$$
这样是可以继续简化的,就是将
$$
\xi_i = 1-y_i(W^Tx_i + b), \xi_i \geq 0
$$
目标函数就变成了
$$
\min\limits_{W,b}\frac{1}{2}|W|^2 + C\sum\limits_{i=1}^n\xi_i \\
s.t. y_i(W^Tx_i + b) \geq 1 - \xi_i,i=1,2,\dots,n \\
\xi_i \geq 0
$$
上面这个就是软间隔SVM的目标函数,它的求解与上面的硬间隔SVM是一样的。软间隔SVM是允许有一点点错误的数据存在,但是如果数据完全不是线性可分的呢,那么上面的方法都无法解决,那该如何?
核函数
我们来看一个经典的异或问题,
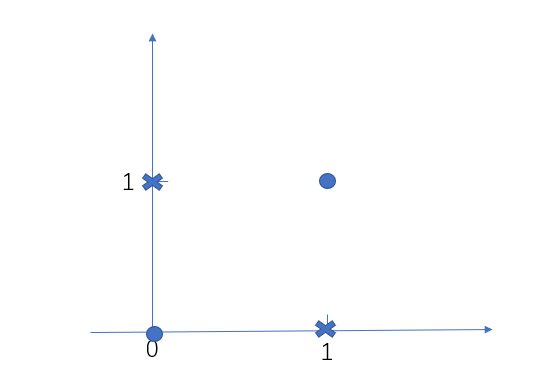
图10. 异或问题
图中有四个点,原点为一类,叉点为一类,这些数据就不是线性可分,那么上面的SVM不能应用到这类数据中,这样的话,我们辛辛苦苦推导了那么久的SVM,原来这么鸡肋,因为现实中还有更复杂的数据,SVM难道都不行吗?我们先来看这个异或问题该如何解决,SVM所处理的数据肯定是线性可分的,这一点无法改变,那我们能不能改变其他方面,比如将这些线性不可分的点变成线性可分的点,可以试一试,毕竟实践出真知,我们将二维变成三维,再加上一个特征,这个特征值为$(x_1 - x_2)^2$,那么其中的叉点变成了(0,1,1)和(1,0,1),圆点变成了(0,0,0)和(1,1,0),画出这个三维图像就是
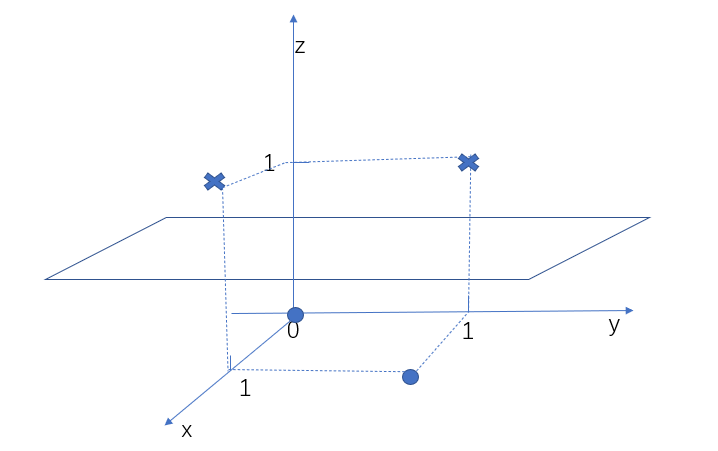
图10. 异或问题
我们可以看到三维之后,数据就变得线性可分了,这也是cover定理,高维比低维更易线性可分,那么我们可以直接在SVM中将数据更成高维,让它变得线性可分,这种利用高维线性可分的方法也被称为核方法,我们将$\phi(x)$称为数据变成高维的方法,那么所有的数据$x$都要变成$\phi(x)$,我们上面求出SVM的最终解就变成了
$$
\max\limits_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_ix_i^T\lambda_jy_jx_j + \sum\limits_{i=1}^{n}\lambda_i \to \max\limits_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\lambda_iy_i\phi(x_i)^T\lambda_jy_j\phi(x_j) + \sum\limits_{i=1}^{n}\lambda_i \notag
$$
在很多实际的应用中,$\phi(x)$函数需要将数据变成很高的维度甚至无限维,这样的话,$\phi(x)$的计算就会变得很复杂,一旦复杂,就很难计算,式中需要先计算$\phi(x_i)^T$,再计算$\phi(x_j)$,最后还要计算俩个式子的乘机$\phi(x_i)^T\phi(x_j)$。一看就知道很复杂,那么我能不能直接计算出$\phi(x_i)^T\phi(x_j)$的值呢,不用计算其中的$\phi(x_i)^T$和$\phi(x_j)$,当然也是可以的,这种直接计算的技巧被称为核技巧,那么我们定义出
$$
K(x_i,x_j) = \phi(x_i)^T\phi(x_j) = <\phi(x_i), \phi(x_j)>
$$
其中$<>$代表内积,$K(x_i,x_j)$就被称为核函数,在很多文献中也会严格的称它为正定核函数,而一般核函数的定义就是
$$
K: \chi \times \chi \to R \\
\forall x,z \in \chi,称K(x,z)为核函数
$$
可以看出一般核函数只要是能将数据映射到实数域中就可以了,并不要求是某个函数的内积。而正定核函数是要求内积的,定义就是
$$
K: \chi \times \chi \to R, \forall x,z \in \chi,有K(x,z), \\
如果\exists \phi: \chi \to R, 并且\phi \in 希尔伯特空间, \\
K(x,z) = <\phi(x), \phi(z)>,那么称K(x,z)为正定核函数.
$$
那么我们怎么证明一个函数是正定核函数呢?不能用定义来证明啊,也无法证明,那么就有了下面的条件
$$
K: \chi \times \chi \to R, \forall x,z \in \chi,有K(x,z), \\
如果K(x,z)满足对称性和正定性,那么K(x,z)就是正定核函数。
$$
其中的对称性就是$K(x,z) = K(z,x)$,而正定性就是任意取N个元素,都是属于$\chi$,对应的gram matrix是半正定的,而其中的gram matrix就是$G = [K(x_i,x_j)]$,下面就是数学知识了,先来看希尔伯特空间,可能一上来就说希尔伯特空间比较懵,我们先来看最简单的线性空间,线性空间只定义了数乘与加法,但是我们想研究向量的长度怎么办,就加入范式,还想研究向量的角度怎么办,就加入内积,变成了内积空间,如果我们还想研究收敛性,就要定义完备性,而完备的内积空间就是希尔伯特空间,完备性就是空间函数的极限还是在希尔伯特空间中,内积也是有对称性、正定性和线性,其中的对称性也是上面那种,$
= $,正定性就是$ \geq 0$,并且等于0的情况只有f = 0,线性就是$ = r_1+ r_2$。
这里我们例举出几个常见的核函数,对于这方面,我的了解也不是很深,
- 线性核,\(K(x_i,x_j) = x_i^Tx_j\),其实就是没核,还是以前样子。
- 多项式核,\(K(x_i,x_j) = (x_ix_j + R)^d\),R代表一个设定的数,d就是次方,当d=1的时候,就是线性核。
- 高斯核,也称为RBF核,\(K(x_i,x_j) = e^{-\frac{|x_i - x_j|^2}{2\sigma^2}}\),这是最常用的核函数。
- 拉普拉斯核,\(K(x_i,x_j) = e^{-\frac{|x_i - x_j|}{\sigma}}\)。
- sigmoid核,\(K(x_i,x_j) = tanh(\beta x_i^Tx_j + \theta)\)。
下面我们看一下最常见的RBF核函数是如何将数据变成无限维的,其中用到了泰勒公式
\[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots = \sum\limits_{n=0}^{N}\frac{x^n}{n!}
\]
推导如下:
\[\begin{align}
K(x_i,x_j) & = e^{-\frac{|x_i - x_j|^2}{2\sigma^2}} \notag \\
& = e^{-\frac{x_i^2}{2\sigma^2}} e^{-\frac{x_j^2}{2\sigma^2}} e^{\frac{x_ix_j}{\sigma^2}} \notag \\
& = e^{-\frac{x_i^2}{2\sigma^2}} e^{-\frac{x_j^2}{2\sigma^2}} \sum\limits_{n=0}^{N}\frac{(\frac{x_ix_j}{\sigma^2})^n}{n!} \notag \\
& = \sum\limits_{n=0}^{N} \frac{1}{n!\sigma^{2n}} e^{-\frac{x_i^2}{2\sigma^2}}x_i^n e^{-\frac{x_j^2}{2\sigma^2}}x_j^n \notag \\
& = \sum\limits_{n=0}^{N}(\frac{1}{n!\sigma^{2n}} e^{-\frac{x_i^2}{2\sigma^2}}x_i^n)( \frac{1}{n!\sigma^{2n}}e^{-\frac{x_j^2}{2\sigma^2}}x_j^n) \notag \\
& = \phi(x_i)^T\phi(x_j)
\end{align}
\]
从上面可以看出RBF核函数已经将\(x_i\)和\(x_j\)变成了无限维的
\[x_i = e^{-\frac{x_i^2}{2\sigma^2}}(1,\frac{x_i}{\sigma^2},\frac{x_i^2}{2\sigma^{2\times 2}},\dots)
\]
核函数不只是在SVM中应用到,其他机器学习模型中也会用到核函数这一概念,毕竟它的思想都是通用,就是高维比低维更加线性可分。
总结
支持向量机在我的研究中用的很少,主要我一直认为它只用于二分类中,并且我一直对核函数并没有深入的了解过,对于SVM最新的发展研究也没有关注过,以前用过一次,就用到我的集成模型中作为我的基学习器,并且也用到了SVM的增量学习,其实我看的是一个中文文献中的SVM增量学习,算法也是非常简单,主要还是看后来的数据是不是支持向量,但是后来那个模型失败了,就没搞过SVM。本文中所有的代码都在我的github。














