[题解]UVA11722

数形结合好题

转化

设你在\(x\)时间到达，你的朋友在\(y\)时间到达

显然\(|y-x| \leqslant w\)时，可以见面

即\(x-w \leqslant y \leqslant x + w\)

于是我们把它们\(x\)和\(y\)变成坐标放到平面直角坐标系里去手绘不易aaaa

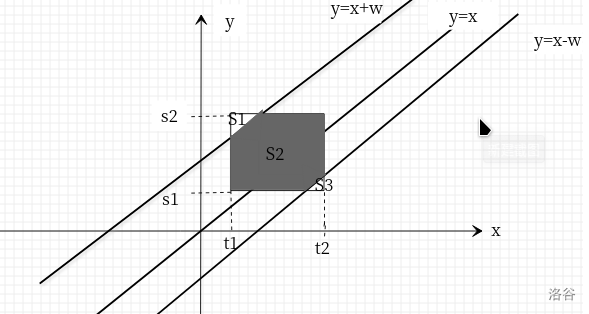
要求的概率就是\(\frac{S_2}{S_1 + S_2 + S_3}\)

我们可以把它继续转化为\(\frac{(S_2 + S_1) - S_1}{S_{长方形}}\)

而\(S_2 + S_1\)便是直线\(y=x-w\)上方与正方形的交

\(S_1\)便是直线\(y=x+w\)上方与正方形的交

问题转化为求直线上方与正方形面积的交

解决

画一个图，分类讨论即可

总共六种情况，如图

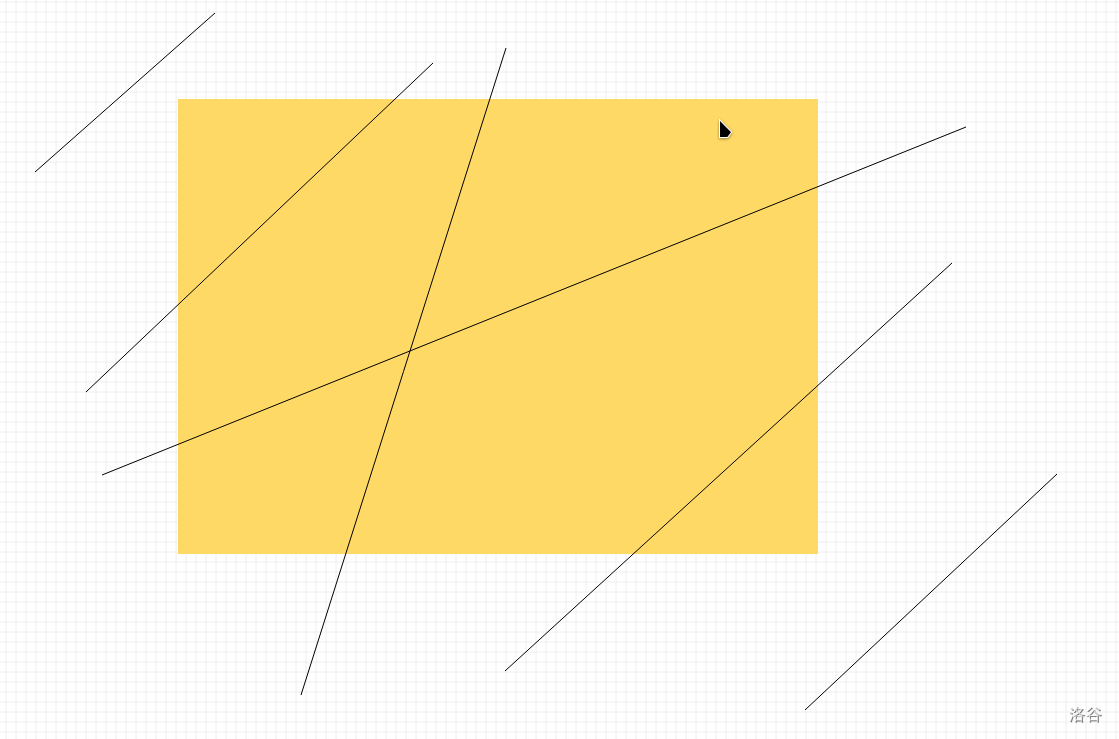
在这张图里看上去每条直线的斜率不一样，但其实本质上它们斜率相同，是长方形的形状不同

代码

#include <cstdio>
typedef double db;

int T, cnt;
db t1, t2, s1, s2, w;

db get(db b) // y = x + b;
{
    if (t1 + b >= s2) return 0;
    if (t1 + b >= s1)
    {
        if (s2 - b <= t2) return 0.5 * (s2 - t1 - b) * (s2 - b - t1);
        return 0.5 * (t2 - t1) * (s2 - t2 - b + s2 - t1 - b);       
    }
    if (s2 - b <= t2) return 0.5 * (s2 - s1) * (s2 - b - t1 + s1 - b - t1);
    if (t2 + b > s1) return (t2 - t1) * (s2 - s1) - 0.5 * (t2 - s1 + b) * (t2 - s1 + b); 
    return (t2 - t1) * (s2 - s1);
}

int main()
{
    scanf ("%d", &T);
    while (T--)
    {
        scanf ("%lf%lf%lf%lf%lf", &t1, &t2, &s1, &s2, &w);
        printf ("Case #%d: %.8lf\n", ++cnt, (get(-w) - get(w)) / ((t2 - t1) * (s2 - s1)));
    }
    return 0;
}