cf(找规律,模拟)
A schoolboy named Vasya loves reading books on programming and mathematics. He has recently read an encyclopedia article that described the method of median smoothing (or median filter) and its many applications in science and engineering. Vasya liked the idea of the method very much, and he decided to try it in practice.
Applying the simplest variant of median smoothing to the sequence of numbers a1, a2, ..., an will result a new sequence b1, b2, ..., bnobtained by the following algorithm:
- b1 = a1, bn = an, that is, the first and the last number of the new sequence match the corresponding numbers of the original sequence.
- For i = 2, ..., n - 1 value bi is equal to the median of three values ai - 1, ai and ai + 1.
The median of a set of three numbers is the number that goes on the second place, when these three numbers are written in the non-decreasing order. For example, the median of the set 5, 1, 2 is number 2, and the median of set 1, 0, 1 is equal to 1.
In order to make the task easier, Vasya decided to apply the method to sequences consisting of zeros and ones only.
Having made the procedure once, Vasya looked at the resulting sequence and thought: what if I apply the algorithm to it once again, and then apply it to the next result, and so on? Vasya tried a couple of examples and found out that after some number of median smoothing algorithm applications the sequence can stop changing. We say that the sequence is stable, if it does not change when the median smoothing is applied to it.
Now Vasya wonders, whether the sequence always eventually becomes stable. He asks you to write a program that, given a sequence of zeros and ones, will determine whether it ever becomes stable. Moreover, if it ever becomes stable, then you should determine what will it look like and how many times one needs to apply the median smoothing algorithm to initial sequence in order to obtain a stable one.
The first input line of the input contains a single integer n (3 ≤ n ≤ 500 000) — the length of the initial sequence.
The next line contains n integers a1, a2, ..., an (ai = 0 or ai = 1), giving the initial sequence itself.
If the sequence will never become stable, print a single number - 1.
Otherwise, first print a single integer — the minimum number of times one needs to apply the median smoothing algorithm to the initial sequence before it becomes is stable. In the second line print n numbers separated by a space — the resulting sequence itself.
4 0 0 1 1
0 0 0 1 1
5 0 1 0 1 0
2 0 0 0 0 0
In the second sample the stabilization occurs in two steps: 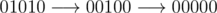 ,
and the sequence 00000 is obviously stable.
,
and the sequence 00000 is obviously stable.
刚开始写的模拟tle了T_T,无语中。。。复杂度相当高。。。。
后来自己找了一些规律可是自己没有发掘出来,看了一下别人代码,可是并没有看懂,不过自己在看完别人代码之后自己对题目的认识更加深入了,对自己找出来的规律有了一点思绪,然后只需要考虑010101010这样交错的情况,然后找到规律了还被自己坑了wa两遍。。。。
先贴那个tle的:
#include <iostream>
#include <cstdio>
#include <cstring>
#include<algorithm>
using namespace std;
int a[500010],b[500010];
int main()
{
int n;
scanf("%d",&n);
bool flag=1;
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
if(i>=2&&a[i]==a[i-2]&&a[i]!=a[i-1])
b[i-1]=!a[i-1],flag=0;
else
b[i-1]=a[i-1];
}
b[0]=a[0],b[n-1]=a[n-1];
if(flag)
{
printf("0\n%d",a[0]);
for(int i=1;i<n;i++)
printf(" %d",a[i]);printf("\n");
}
else
{
int sum=0;
while(!flag)
{
sum++;
flag=1;
for(int i=0;i<n;i++)
a[i]=b[i];
for(int i=0;i<n;i++)
if(i>=2&&a[i]==a[i-2]&&a[i]!=a[i-1])
b[i-1]=!a[i-1],flag=0;
else
b[i-1]=a[i-1];
b[0]=a[0],b[n-1]=a[n-1];
}
printf("%d\n%d",sum,a[0]);
for(int i=1;i<n;i++)
printf(" %d",a[i]);printf("\n");
}
return 0;
}下面是ac代码(复杂度直接就是o(n)了,找到规律就是快):
#include <iostream>
#include <cstdio>
#include <cstring>
#include<algorithm>
using namespace std;
int a[500010],b[500010];
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
b[0]=a[0],b[n-1]=a[n-1];
int max0=0,j;
for(int i=1;i<n-1;i++)
{
if(a[i]!=a[i-1]&&a[i]!=a[i+1])
{
int jl=1;
for(j=i+2;j<n;j++)
if(a[j]==a[j-2])
jl++;
else
break;
if(jl%2==0)
{
if(jl/2>max0)
max0=jl/2;
for(int k=i;k<i+jl/2;k++)
{b[k]=a[i-1];}
for(int k=i+jl/2;k<i+jl;k++)
{b[k]=a[i+jl];}
}
else
{
if((jl+1)/2>max0)
max0=(jl+1)/2;
for(int k=i;k<i+jl;k++)
{b[k]=a[i-1];}
}
i=j-2;//cout<<"i"<<i<<endl;
}
else b[i]=a[i];
}
printf("%d\n%d",max0,b[0]);
for(int i=1;i<n;i++)
printf(" %d",b[i]);printf("\n");
return 0;
}



