cf(405A,B,C,D)
Little Chris is bored during his physics lessons (too easy), so he has built a toy box to keep himself occupied. The box is special, since it has the ability to change gravity.
There are n columns of toy cubes in the box arranged in a line. The i-th column contains ai cubes. At first, the gravity in the box is pulling the cubes downwards. When Chris switches the gravity, it begins to pull all the cubes to the right side of the box. The figure shows the initial and final configurations of the cubes in the box: the cubes that have changed their position are highlighted with orange.

Given the initial configuration of the toy cubes in the box, find the amounts of cubes in each of the n columns after the gravity switch!
The first line of input contains an integer n (1 ≤ n ≤ 100), the number of the columns in the box. The next line contains n space-separated integer numbers. The i-th number ai (1 ≤ ai ≤ 100) denotes the number of cubes in the i-th column.
Output n integer numbers separated by spaces, where the i-th number is the amount of cubes in the i-th column after the gravity switch.
4 3 2 1 2
1 2 2 3
3 2 3 8
2 3 8
The first example case is shown on the figure. The top cube of the first column falls to the top of the last column; the top cube of the second column falls to the top of the third column; the middle cube of the first column falls to the top of the second column.
In the second example case the gravity switch does not change the heights of the columns.
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long ll;
bool a[110][110]={{0}};
int main()
{
int n,m;
cin>>n;
for(int i=0;i<n;i++)
{
int t;
cin>>t;
m= i==0? t:max(m,t);
for(int j=0;j<t;j++)
a[i][j]=1;
}
for(int i=0;i<m;i++)
{
int s=0;
for(int j=0;j<n;j++)
if(a[j][i])s++,a[j][i]=0;
for(int j=n-1;j>=0&&s>0;j--,s--)
a[j][i]=1;
}
for(int i=0;i<n;i++)
{
int s=0;
for(int j=0;j<m;j++)
s+=a[i][j];
cout<<s<<' ';
}cout<<endl;
return 0;
}
Little Chris knows there's no fun in playing dominoes, he thinks it's too random and doesn't require skill. Instead, he decided to play withthe dominoes and make a "domino show".
Chris arranges n dominoes in a line, placing each piece vertically upright. In the beginning, he simultaneously pushes some of the dominoes either to the left or to the right. However, somewhere between every two dominoes pushed in the same direction there is at least one domino pushed in the opposite direction.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right. When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces. The figure shows one possible example of the process.
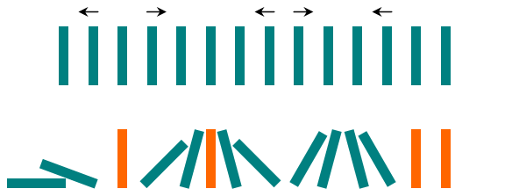
Given the initial directions Chris has pushed the dominoes, find the number of the dominoes left standing vertically at the end of the process!
The first line contains a single integer n (1 ≤ n ≤ 3000), the number of the dominoes in the line. The next line contains a character strings of length n. The i-th character of the string si is equal to
- "L", if the i-th domino has been pushed to the left;
- "R", if the i-th domino has been pushed to the right;
- ".", if the i-th domino has not been pushed.
It is guaranteed that if si = sj = "L" and i < j, then there exists such k that i < k < j and sk = "R"; if si = sj = "R" and i < j, then there exists such k that i < k < j and sk = "L".
Output a single integer, the number of the dominoes that remain vertical at the end of the process.
14 .L.R...LR..L..
4
5 R....
0
1 .
1
The first example case is shown on the figure. The four pieces that remain standing vertically are highlighted with orange.
In the second example case, all pieces fall down since the first piece topples all the other pieces.
In the last example case, a single piece has not been pushed in either direction.
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long ll;
char a[3010];
bool aa[3010]={0};
int main()
{
int n;
cin>>n;
cin>>a;
int sum=0;
for(int i=0;i<n;i++)
if(!aa[i]&&a[i]=='R')
{
aa[i]=1;
int s=i,e=-1,j;
for(j=i+1;j<n;j++)
if(a[j]=='L')
{
aa[j]=1;
e=j;
break;
}
else aa[j]=1;
if(e!=-1)
{
if((e-s+1)%2==1)
sum++;
}
i=j;
}
else if(a[i]=='L'&&!aa[i])
{
aa[i]=1;
for(int j=i-1;j>=0;j--)
aa[j]=1;
}
for(int i=0;i<n;i++)
{
//cout<<aa[i]<<' ';
if(!aa[i])sum++;
}
cout<<sum<<endl;
return 0;
}
Little Chris is a huge fan of linear algebra. This time he has been given a homework about the unusual square of a square matrix.
The dot product of two integer number vectors x and y of size n is the sum of the products of the corresponding components of the vectors. The unusual square of an n × n square matrix A is defined as the sum of n dot products. The i-th of them is the dot product of the i-th row vector and the i-th column vector in the matrix A.
Fortunately for Chris, he has to work only in GF(2)! This means that all operations (addition, multiplication) are calculated modulo 2. In fact, the matrix A is binary: each element of A is either 0 or 1. For example, consider the following matrix A:
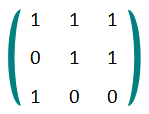
The unusual square of A is equal to (1·1 + 1·0 + 1·1) + (0·1 + 1·1 + 1·0) + (1·1 + 0·1 + 0·0) = 0 + 1 + 1 = 0.
However, there is much more to the homework. Chris has to process q queries; each query can be one of the following:
- given a row index i, flip all the values in the i-th row in A;
- given a column index i, flip all the values in the i-th column in A;
- find the unusual square of A.
To flip a bit value w means to change it to 1 - w, i.e., 1 changes to 0 and 0 changes to 1.
Given the initial matrix A, output the answers for each query of the third type! Can you solve Chris's homework?
The first line of input contains an integer n (1 ≤ n ≤ 1000), the number of rows and the number of columns in the matrix A. The next nlines describe the matrix: the i-th line contains n space-separated bits and describes the i-th row of A. The j-th number of the i-th line aij(0 ≤ aij ≤ 1) is the element on the intersection of the i-th row and the j-th column of A.
The next line of input contains an integer q (1 ≤ q ≤ 106), the number of queries. Each of the next q lines describes a single query, which can be one of the following:
- 1 i — flip the values of the i-th row;
- 2 i — flip the values of the i-th column;
- 3 — output the unusual square of A.
Note: since the size of the input and output could be very large, don't use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.
Let the number of the 3rd type queries in the input be m. Output a single string s of length m, where the i-th symbol of s is the value of the unusual square of A for the i-th query of the 3rd type as it appears in the input.
3 1 1 1 0 1 1 1 0 0 12 3 2 3 3 2 2 2 2 1 3 3 3 1 2 2 1 1 1 3
01001
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long ll;
int a[1010][1010];
int main()
{
int n;int x=0;
scanf("%d",&n);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
scanf("%d",&a[i][j]);
if(i==j&&a[i][j]==1)x=!x;
}
int q;scanf("%d",&q);
while(q--)
{
int t;scanf("%d",&t);
if(t!=3)
{
int tt;scanf("%d",&tt);
if(t==1)
x=!x;
else
x=!x;
}
else
printf("%d",x);
}
return 0;
}
Little Chris is very keen on his toy blocks. His teacher, however, wants Chris to solve more problems, so he decided to play a trick on Chris.
There are exactly s blocks in Chris's set, each block has a unique number from 1 to s. Chris's teacher picks a subset of blocks X and keeps it to himself. He will give them back only if Chris can pick such a non-empty subset Y from the remaining blocks, that the equality holds:

For example, consider a case where s = 8 and Chris's teacher took the blocks with numbers 1, 4 and 5. One way for Chris to choose a set is to pick the blocks with numbers 3 and 6, see figure. Then the required sums would be equal:(1 - 1) + (4 - 1) + (5 - 1) = (8 - 3) + (8 - 6) = 7.

However, now Chris has exactly s = 106 blocks. Given the set X of blocks his teacher chooses, help Chris to find the required set Y!
The first line of input contains a single integer n (1 ≤ n ≤ 5·105), the number of blocks in the set X. The next line contains n distinct space-separated integers x1, x2, ..., xn (1 ≤ xi ≤ 106), the numbers of the blocks in X.
Note: since the size of the input and output could be very large, don't use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.
In the first line of output print a single integer m (1 ≤ m ≤ 106 - n), the number of blocks in the set Y. In the next line output m distinct space-separated integers y1, y2, ..., ym (1 ≤ yi ≤ 106), such that the required equality holds. The sets X and Y should not intersect, i.e.xi ≠ yj for all i, j (1 ≤ i ≤ n; 1 ≤ j ≤ m). It is guaranteed that at least one solution always exists. If there are multiple solutions, output any of them.
3 1 4 5
2 999993 1000000
1 1
1 1000000
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long ll;
bool x[1000005]={0};
const int s=1000001;
int main()
{
int n,sum=0;
cin>>n;
for(int i=0;i<n;i++)
{int t;cin>>t;x[t]=1;if(x[s-t]==1)sum++;}
printf("%d\n",n);
for(int i=1;i<s;i++)
if(sum&&!x[i]&&!x[s-i])
sum--,cout<<i<<' '<<s-i<<' ';
else if(x[i]&&!x[s-i])
cout<<s-i<<' ';
cout<<endl;
return 0;
}



