hdu4568(spfa,状态压缩dp)
Hunter
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1668 Accepted Submission(s): 501
Problem Description
One day, a hunter named James went to a mysterious area to find the treasures. James wanted to research the area and brought all treasures that he could.
The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.
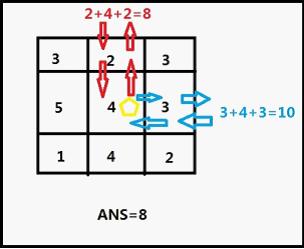
The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.

Input
The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case begins with a line containing 2 integers N M , (1<=N,M<=200), that represents the rectangle. Each of the following N lines contains M numbers(0~9),represent
the cost of each point. Next is K(1<=K<=13),and next K lines, each line contains 2 integers x y means the position of the treasures, x means row and start from 0, y means column start from 0 too.
Output
For each test case, you should output only a number means the minimum cost.
Sample Input
2 3 3 3 2 3 5 4 3 1 4 2 1 1 1 3 3 3 2 3 5 4 3 1 4 2 2 1 1 2 2
Sample Output
8 11
题目大意:给定一个n*m的棋盘,每一个格子有一个值,代表经过这个格子的花费,给出sum个宝藏点的坐标,求从棋盘的任意一个边进入棋盘,经过所有的宝藏点后在走出
棋盘所需要的最小花费
解题思路:spfa处理处任意两个宝藏点之间的最短距离(最小花费)和每个宝藏点和边界的最短距离。然后状态压缩:dp[s][i]表示经过宝藏点的状态为s并且结尾点为i的
最小花费
刚开始老是超时。。。。结果发现原来是模拟队列数组开的太小了。。。。无言以对T_T
代码里面注释都写得非常清楚了,便于理解。//由于自己比较熟练spfa所以没写spfa的注释
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
using namespace std;
typedef long long ll;
const int N=205,INF=999999999;
int n,m,k;
int a[N][N];///图上每个点的cost
int fx[4][2]= {{1,0},{0,1},{-1,0},{0,-1}}; ///方向数组
int dis[N][N];///spfa时图上每两点之间的最短路
int mi[N][N];///存储宝藏点之间的最短路
int dd[N];///宝藏某个点到达边界的最短距离
int dp[1<<14][14];///表示经过宝藏点的状态为s并且结尾点为i的最小花费
struct data
{
int x,y;
} p[N]; ///有宝藏的点
struct hh
{
int x,y;
} dl[99999999]; ///模拟队列!!注意!!!队列一定要设置的足够大!!!!刚开始设置小了老是超时。。。
void spfa(int s)
{
for(int i=0; i<n; i++)
for(int j=0; j<m; j++)
dis[i][j]=INF;
dis[p[s].x][p[s].y]=0;
bool vis[N][N]= {{0}};
int r=0,l=0;
dl[r].x=p[s].x,dl[r++].y=p[s].y;
while(l<r)
{
int x=dl[l].x,y=dl[l++].y;
vis[x][y]=0;
if(x==0||x==(n-1)||y==0||y==(m-1))
dd[s]=min(dd[s],dis[x][y]);
for(int i=0; i<4; i++)
{
int tx=x+fx[i][0],ty=y+fx[i][1];
if(tx>=0&&ty>=0&&tx<n&&ty<m&&a[tx][ty]!=-1)
{
if(dis[x][y]+a[tx][ty]<dis[tx][ty])
{
dis[tx][ty]=dis[x][y]+a[tx][ty];
if(!vis[tx][ty])
{
vis[tx][ty]=1;
dl[r].x=tx,dl[r++].y=ty;
}
}
}
}
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
for(int i=0; i<n; i++)
for(int j=0; j<m; j++)
scanf("%d",&a[i][j]);
scanf("%d",&k);
for(int i=0; i<k; i++)
scanf("%d%d",&p[i].x,&p[i].y);
for(int i=0; i<k; i++)
for(int j=0; j<k; j++)
mi[i][j]=i==j?0:INF;
for(int i=0; i<N; i++)
dd[i]=INF;
for(int i=0; i<1<<k; i++)
for(int j=0; j<k; j++)
dp[i][j]=INF;
for(int i=0; i<k; i++)
{
spfa(i);
for(int j=0; j<k; j++)
if(i!=j)
mi[i][j]=min(mi[i][j],dis[p[j].x][p[j].y]);
dp[1<<i][i]=dd[i]+a[p[i].x][p[i].y];///dp入口,就是从某个点进去需要花费的最短路程
}
for(int i=0; i<1<<k; i++)
{
for(int j=0; j<k; j++)
{
if((i&(1<<j))&&dp[i][j]!=INF)///i&(1<<j)不等于0(见上面我对dp[][]的定义,以j结尾那么i状态肯定要包含j),dp[i][j]不等于INF
for(int kk=0; kk<k; kk++)
{
if((i&(1<<kk))==1)continue;///这用来表示状态dp[i][j]的下一个状态dp[i|(1<<kk)][kk],因为它是以kk这个点结尾的,所以它的上一个状态不应该有kk这个点存在
dp[i|(1<<kk)][kk]=min(dp[i|(1<<kk)][kk],dp[i][j]+mi[j][kk]);///mi[j][kk]是spfa提前已经算好了
}
}
}
int ans=INF;
for(int i=0; i<k; i++)
ans=min(ans,dp[(1<<k)-1][i]+dd[i]);///(1<<k)-1表示所有宝藏点都走过了,以i结尾就加上宝藏点到边界的最短路程
printf("%d\n",ans);
}
return 0;
}
持续更新博客地址:
blog.csdn.net/martinue



