hdu4587(去掉两个点让强连通分量最大)
TWO NODES
Time Limit: 24000/12000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)Total Submission(s): 1702 Accepted Submission(s): 530
Problem Description
Suppose that G is an undirected graph, and the value of stab is defined as follows:
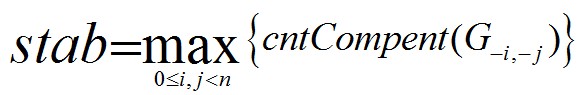
Among the expression,G-i, -j is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.
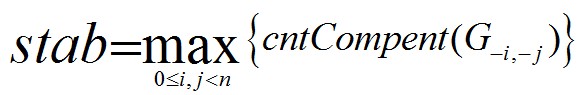
Among the expression,G-i, -j is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.
Input
The input will contain the description of several graphs. For each graph, the description consist of an integer N for the number of nodes, an integer M for the number of edges, and M pairs of integers for edges (3<=N,M<=5000).
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.
Output
For each graph in the input, you should output the value of stab.
Sample Input
4 5 0 1 1 2 2 3 3 0 0 2
Sample Output
2
题意:去掉两个点,让原图的强连通分量最大。
思路:暴力解决这题真的够呛。。所以先去枚举掉一个点,然后用tarjan判断割点的方法,如果被判断为割点说明强连通分量要增加一了,存到cut数组里,最后算最大值就好了。
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<stack>
using namespace std;
typedef long long ll;
const int N=5010;
struct data
{
int to,next;
} tu[N*N];
int head[N],low[N],dfn[N];///dfn[]记录某个点被访问到的次数,low[]记录某个点或其子树回边的最小步数的点
int cut[N];///是否为割点且该点连接边的数量
int ip;
int step,rt_son,scc_cnt;
void init()
{
ip=0;
memset(head,-1,sizeof(head));
}
void add(int u,int v)
{
tu[ip].to=v,tu[ip].next=head[u],head[u]=ip++;
}
void tarjan(int u,int del)
{
//cout<<u<<' ';
dfn[u] = low[u] = step++;
for(int i = head[u]; i!=-1 ; i=tu[i].next)
{
int to = tu[i].to;
if(to==del)continue;
if(!dfn[to])///表示未被访问的点
{
tarjan(to,del);
low[u]=min(low[u],low[to]);
if(low[to]>=dfn[u])
cut[u]++;
}
else
low[u]=min(low[u],dfn[to]);
}
}
void solve(int n)
{
int ans=0;
for(int j=1; j<=n; j++)
{
memset(dfn, 0, sizeof(dfn));
for(int i=1; i<=n; i++)
cut[i]=1;
step = 1;
int sum=0;
for (int i = 1; i <=n; i++)
if (i!=j&&!dfn[i])
{
sum++;
cut[i]=0;
tarjan(i,j);
}
for(int i=1; i<=n; i++)
if(i!=j)
ans=max(ans,sum+cut[i]-1);
}
printf("%d\n",ans);
}
int main()
{
int m,n;
while(~scanf("%d%d",&n,&m))
{
init();
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
a++,b++;
add(a,b);
add(b,a);
}
solve(n);
}
return 0;
}
持续更新博客地址:
blog.csdn.net/martinue



