多重比较方法
前篇讲的是两个总体样本之间的比较方法,如果有多个处理水平,通常使用三种常见的方法,最小显著差数法(LSD法)、复极差法(q法)和Duncan氏新复极差法(SSR法)。本质上都属于t检验法。因此,使用这三种方法必须满足方差齐性。如果通过F检验p>0.05,方差具有齐次性。
具体操作方法可参考:
http://www.wendangku.net/doc/a8901b87bceb19e8b8f6ba42-2.html
例如,一个试验中k个处理平均数间可能有k(k-1)/2个比较,因而这种比较是复式比较亦称为多重比较(multiple comparisons)。
进行方差分析时需要满足独立样本、方差齐性、正态分布等条件,如果方差不具备齐性(F检验),
可首先进行数据转换,如通过对数变换、平方根变换、倒数变换、平方根反正弦变换等方法变换后再进行方差齐性检验,若还不行只能进行非参数检验。
1:最小显著差数法(least significant difference,简称LSD法),LSD 法实质上是t测验。
其程序是:在处理间的F测验为显著的前提下,计算出显著水平为α的最小显著差数;任何两个平均数的差数如其绝对值≥,即为在α水平上显著;反之则为不显著。
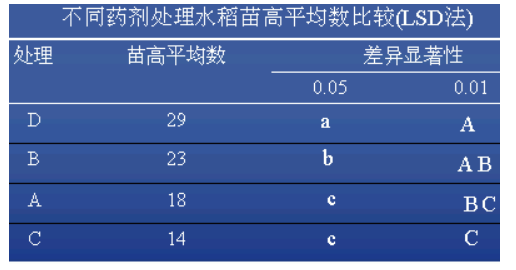
举例:试以LSD法测验各种药剂处理的苗高平均数之间的差异显著性。


下面用字母标记法对各种药剂处理的苗高平均数之间的差异显著性进行比较。首先约定:
(1)5%水平的差异显著性用小写英文字母标记,1%水平的差异显著性用大写英文字母标记;
(2)若两平均数之间差异显著用不同字母标记,若两平均数之间差异不显著用相同字母标记。
2:复极差法(q法)
LSD法的t测验是根据两个样本平均数差数(k=2)的抽样分布提出来的,但是一组处理(k>2)是同时抽取k个样本的结果。抽样理论提出k=2时与k>2时,例如k=10时其随机极差是不同的,随着k的增大而增大,因而用k=2时的t测验有可能夸大k=10时最大与最小两个样本平均数差数的显著性。基于极差的抽样分布理论,Student-Newman-Keul提出了q测验或称复极差测验,有时又称SNK测验(SAS软件中就是这种叫法)或NK测验。
q测验方法是将一组k个平均数由大到小排列后,根据所比较的两个处理平均数的差数是几个平均数间的极差分别确定最小显著极差的。
q测验因是根据极差抽样分布原理,其各个比较都可保证同一个α水平。其尺度构成为:

式中2≤p≤k,p是所有比较的平均数按大到小顺序排列所计算出的两极差范围内所包含的平均数个数(称为秩次距),SE为平均数的标准误。
3:新复极差法
q法不同秩次距p下的最小显著极差变幅大,虽然减小了犯α错误的概率,但同时增加了犯β错误的概率。为此,D.B.Duncan(1955)提出了新复极差法,又称最短显著极差法(shortest significant ranges SSR)、
Duncan法。该法与q法(SNK法)相似,其区别在于计算最小显著极差时不是查q表而是查SSR表,所得最小显著极差值随着k增大通常比q测验时减小。

多重比较方法的选择
1、试验事先确定比较的标准,凡是与对照相比较,或与预定要比较的对象比较,一般可选用最小显著差数法;
2、根据否定一个正确的H 0 和接受一个不正确的H 0 的相对重要性来决定。
三种方法的显著尺度不同,LSD法最低,SSR法次之,q法最高。故LSD测验犯α错误的概率最大,q法最小,SSR法介于两者之间,因此,对于试验结论事关重大或有严格要求的,宜用q法;一般试验可用SSR法。
实际研究中,经常需要比较两组以上样本均数的差别,这时不能使用t检验方法作两两间的比较(如有人对四组均数的比较,作6次两两间的t检验),这势必增加两类错误的可能性(如原先a定为0.05,这样作多次的t检验将使最终推断时的a>0.05)。故对于两组以上的均数比较,必须使用方差分析的方法,当然方差分析方法亦适用于两组均数的比较。方差分析可调用此过程可完成。
Least-significant difference(LSD):最小显著差法。a可指定0~1之间任何显著性水平,默认值为0.05;
Bonferroni:Bonferroni修正差别检验法。a可指定0~1之间任何显著性水平,默认值为0.05;
Duncan’s multiple range test:Duncan多范围检验。只能指定a为0.05或0.01或0.1,默认值为0.05;
Student-Newman-Keuls:Student-Newman-Keuls检验,简称N-K检验,亦即q检验。a只能为0.05;(以前都以SNK法最为常用,但研究表明,当两两比较的次数极多时,该方法的假阳性非常高,最终可以达到100%。因此比较次数较多时,包括SPSS和SAS在内的权威统计软件都不再推荐使用此法。)
Tukey’s honestly significant difference:Tukey显著性检验。a只能为0.05;
Tukey’s b:Tukey另一种显著性检验。a只能为0.05;
Scheffe:Scheffe差别检验法。a可指定0~1之间任何显著性水平,默认值为0.05。
根据对相关研究的检索结果,除了参照所研究领域的惯例外,一般可以参照如下标准:
如果存在明确的对照组,要进行的是验证性研究,即计划好的某两个或几个组间(和对照组)的比较,宜用Bonferoni(LSD)法;若需要进行的是多个平均数间的两两比较(探索性研究),且各组样本数相等,宜用Tukey法,其他情况宜用Scheffe法。
另外Equal Variances Not Assumed复选框组提供了方差不齐时可以采用的两两比较方法,一般认为Games-Howell法稍好一些。
不过由于这方面统计学界尚无定论,建议最好直接使用非参数检验方法。
Tukey法:20241103新增 参考https://zhuanlan.zhihu.com/p/44880434
在介绍Tukey方法前,首先了解学生化极差分布。
在概率论和统计学中,学生化极差分布是极差的抽样分布。该分布是一种连续型概率分布,用于在样本量较小且总体标准差未知的情况下估计正态分布总体的极差。
假设要比较的组数为k,那么在零假设成立的条件下,下面的随机变量服从学生化极差分布。
𝑞=𝑋¯𝑚𝑎𝑥−𝑋¯𝑚𝑖𝑛𝑆𝑐2𝑛
公式中分子分别是最大和最小样本的均值, 𝑆𝑐2 是所有样本的联合方差 ,n为每个样本的样本含量。该统计量有两个自由度,分别为k和n-k。
Turkey的HSD (Honestly significant difference)是基于学生化极差的成对比较。其思想和LSD方法类似,通过计算HSD统计量,如果两组均数的差异大于该极差,认为差异是显著的,因此拒绝零假设,认为两组均数不同。计算临界HSD的公式为
𝐻𝑆𝐷=𝑞α(𝑘,ν)𝑆𝑐2𝑛
k为组数,ν为联合方差的自由度,即N-k,n为每个样本的样本含量。从HSD公式上看,Tukey法较LSD法保守,即较LSD不易发现显著差异。Tukey法要求比较的样本容量相差不大,一般用于样本容量相同的组之间均数的比较。
发现显著性的敏感程度 (更容易发现显著差异),LSD法最低,SSR法次之,q法,tukey最高。目前推荐tukey做探索新比较,但是要求组内样本量n相同,HSD计算用到了n。



