[USACO1.5]八皇后 Checker Challenge

题目链接 https://www.luogu.com.cn/problem/P1219

没错我又做的dfs.........因为总感觉没大理解不太会写.......那怎么办嘛......

---

 

对于八皇后问题我们可以把它转化为精确覆盖的问题：

1、每行只能放一个皇后

2、每列只能放一个皇后

3、每个“/”只能放一个皇后

4、每个“\”只能放一个皇后

---

 

本道题最重要的就是记录下皇后占领的格子（打标记的思想），通过标记判断下一个皇后能否在某个位置。如果可以，继续搜索下一个皇后的位置；如果不可以，则清除标记返回上一步，继续搜索。

我的第一想法是用四个一维数组分别表示行、列、左斜、右斜，记录这四条线是否被标记。看到有用二维数组的但是好像会TLE，我也没试。

（还没写完但是实验室要关门了我要走了明天再写！）

（第二天：我已经忘了我想写什么了。。。）

---

 

更：

关于 第21行代码中，对角线和反对角线为什么分别为 i+j 和 i-j+n ？

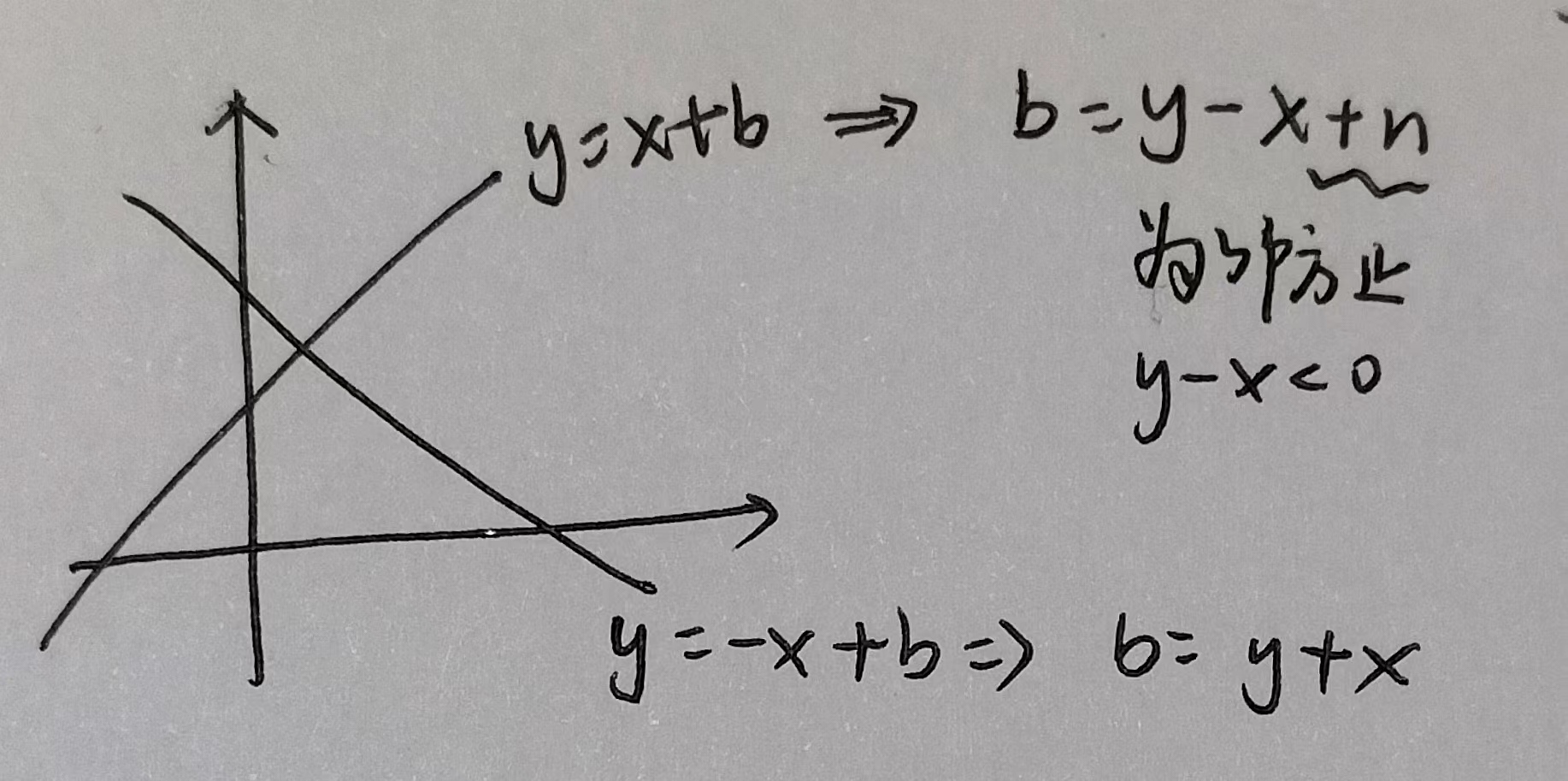
关于 为什么要清除标记？

因为要回溯，对于不能满足条件的点不再进行搜索，并将之前的标记清除，再对下一个点搜索。

---

 

 

放AC代码

#include<bits/stdc++.h>
using namespace std;
int n,sum=0;
int a[50],b[50],c[50],d[50];//——、|、/、'\'
void dfs(int i)
{
    if(i>n)//如果超过n行
    {
        sum++;//表明已经找到一个解，则解的总数+1
        if(sum>3) return;
        else//输出前三个解
        {
            for(int i=1;i<=n;i++)
                cout<<a[i]<<" ";
            cout<<endl;
            return;
        }
    }
    for(int j=1;j<=n;j++)//尝试可能的位置
    {
        if((!b[j])&&(!c[i+j])&&(!d[i-j+n]))//如果纵列和对角线没有都没有被占领
        {
            a[i]=j;//标记第i排是第j个
            b[j]=-1;//占领纵列
            c[i+j]=-1;
            d[i-j+n]=-1;
            dfs(i+1);//深入搜索下一个皇后
            b[j]=0;//清除标记
            c[i+j]=0;
            d[i-j+n]=0;
        }
    }
}
int main()
{
    cin>>n;
    dfs(1);
    cout<<sum;
    return 0;
}