【数据结构】部分易考知识点回顾

期末实验考试一共线性表、树和查找、图、排序四道题。据说需要重点复习二叉树的遍历与哈希表。
目前还没写完，龟速更新中。。。

线性表&栈&队列

顺序栈

表达式求值

核心逻辑

• 核心算法是一个循环，每次读入一个元素：可能是一个数或一个符号（运算符、左右括号和结束符）
• 括号包着的是一个独立的表达式，可以直接看成一个数。因此递归调用求值函数把括号中的内容处理成一个数就可以了。
• 运算优先级低的运算符先保留(存入栈中)，因为不知道第二个操作数后面是否会有更高优先级的运算符，使得第二个操作数发生改变。如1+2*3中，读到+时先按兵不动。
• 进行一次运算，当且仅当：
  • a. 这一次循环读入的不是数字；
  • b. 运算符栈非空（和条件a共同保证目前存在1个运算符和2个操作数）；
  • c. 当前读入的符号为运算符，且优先级低于栈顶符号优先级；或者当前读入的为结束符。（此时上述栈顶运算符的顾虑抵消了，可以进行运算）
• 运算只会取栈顶的运算符和前两个运算数进行运算。

参考代码

// 全部函数采用指针now来读取字符串，并且指针now为引用传参，便于标记读到哪一位了。
// 从当前位置开始，读入字符，将其转化为浮点数并存入到引用变量ans中。(指针now移到这个数后一位(应当是符号))
// 返回值表示是否有读到一个数字。0为没有读入。
inline bool readnum(char *&now,float &ans) 
{
    if(*now<'0' || *now>'9') return 0;
    do
    {
        ans *= 10;
        ans += *now-'0';
        now++;
    } while (*now >= '0' && *now <= '9'); // 转换整数部分
    if (*now == '.')                      // 如果有小数部分，则转换
    {
        now++; //跳过小数点
        float flag=0.1;
        do
        {
            ans += (*now-'0')*flag;
            flag *= 0.1;
            now++;
        } while (*now>='0'&&*now<='9'); // 转换小数部分
    }
    return 1;
}
// 运算优先级比较函数，只考虑了四则运算
inline bool cmp(char a,char b) 
{
    int a1 = (a=='*' || a=='/')?1:0;
    int b1 = (b=='*' || b=='/')?1:0;
    return a1<=b1;
}
// 运算函数，直接从栈中取出运算符与操作数
// 因为该函数调用前，算法可以保证栈里面有元素，没有判断栈是否为空。
// 同样通过引用传参的方式使函数内可以访问栈中元素
inline float calc(Stack<float> &ovs,Stack<char> &optr) 
{
    float b=ovs.top(); ovs.pop();
    float a=ovs.top(); ovs.pop();
    char opt=optr.top();optr.pop();
    switch (opt)
    {
    case '+':
        return a+b;
    case '-':
        return a-b;
    case '*':
        return a*b;
    case '/':
        return a/b;
    default:
        return -1;
    }
}
float deal(char* &now)
{
    // 分别为运算数栈与运算符栈
    Stack<float> ovs(64);
    Stack<char> optr(64);
    while(1)
    {
        if (*now == '(') // 若读到括号，则进入递归，单独处理括号中的内容。
        {
            now++;
            ovs.push(deal(now)); // 处理完后返回，压入运算数栈。
        }

        float num = 0; // 若接下来是一个数，就放进这个变量里，然后再进栈
        if (readnum(now, num))
            ovs.push(num);
        else // 否则说明读到了一个运算符，开始处理表达式
        {
            // 运算符栈不为空，这时候需要比较当前运算符和栈中运算符优先级
            // 栈里面运算符优先级高，就先把它算掉再管当前的运算符
            // 否则先搁置当前运算符，放入运算符栈里面，下一次遇到运算符的时候再管。（以防后面有优先级更高的运算符）
            while (!optr.empty())
            {
                if (cmp(*now, optr.top()))
                    ovs.push(calc(ovs, optr));
                else
                {
                    optr.push(*(now++)); // 这里入栈之后就now++了，表示这个符号处理完了
                    break;
                }
            }
            if (*now == '#' || *now == ')') // 读到这两个说明这一段表达式结束了，退出外层循环。
                break;
            // 如果当前还是个符号，只有可能是因为opt栈是空的，没进入while循环处理掉
            // 说明它是第一个进栈的运算符，先留着
            if ((*now < '0' || *now > '9'))
                optr.push(*(now++));
        }
    }
    // 最后ovs栈里面只可能剩下一个元素，就是运算结果。
    return ovs.top(); 
}

树与二叉树

二叉树

二叉树的存储

• 二叉树的，或者说树的基本单位都是节点(Node)，节点之间的联系构成了树。所以要存储二叉树，只需要存储节点的内容(即数据)和节点之间的关系就可以了。
• 而对于二叉树，因为节点间的关系是有向的父子关系。因此我们不妨把关系统一存在父节点上，即在父节点中留下它的子节点的索引——指针。这样一来一个复杂的二叉树就能够拆解为相对简洁的多个节点进行存储。
  
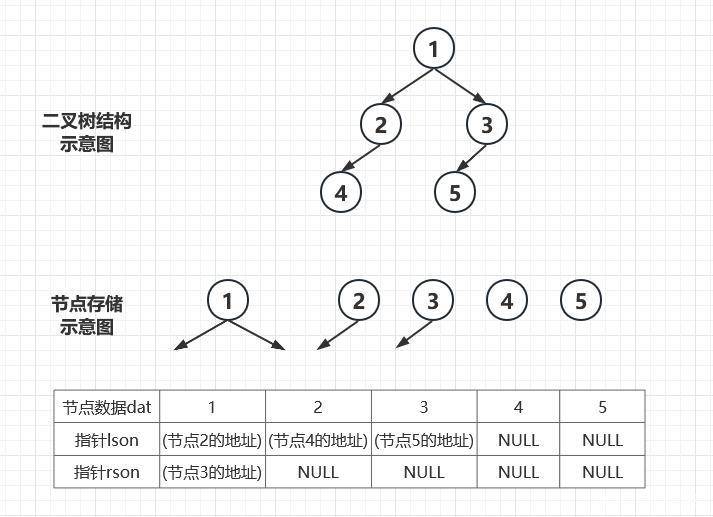
• 单个节点存储的代码，可以使用结构体来实现。在建立二叉树时，每新增一个节点，就使用new新申请一个节点的内存。

struct Node
{
	Node *lson,*rson;
	int dat;
}*Root;
// 新增单个节点，此处仅代表原理演示，实际可以写得更简单
void CreateNode(Node *root, int data, bool flag)
{
	if(root==NULL)
		return;
	Node *now = new Node;
	now->dat = data;
	now->lson = NULL;
	now->rson = NULL;
	
	// flag用于标记是左孩子还是右孩子
	if(flag==0)
		root->lson = now;
	else
		root->rson = now;
}

二叉树的遍历

• 二叉树的遍历方式分为前序遍历、中序遍历、后序遍历三种，区别在于三种遍历方式访问根节点的时机不同。

使用递归方法

• 每一种遍历方式都可以选择是否用递归方式来写。使用递归写遍历算法非常简易，设计一个递归算法可以使用如下的大致思路：
  • 考虑单次调用函数需要使用的参数。 如指向当前根节点的指针root.
  • 设置递归边界。即检测当前节点是否没有子节点。 如果是，则直接返回。
  • 设计访问当前节点并进行处理的代码。 注意只需要考虑对当前节点的处理，后续的节点会在各自被访问到时执行相同的代码。所谓儿孙自有儿孙福。 对于二叉树的遍历，这一操作即访问并输出当前节点的数据。
  • 考虑从当前节点如何转移到下一个节点。 对于二叉树的遍历，即访问当前节点的左右子节点。
• 要想实现前序、中序等区别，只需要调换上述第三和第四部分的代码顺序即可。以下是中序遍历的参考代码。

void trav_in(Node *now)
{
	if(now->dat == '#') // 具体边界视题目而定，有时是now==NULL 等
		return;
	trav_in(now->lson); // 先访问左子树
	cout<<now->dat<<" "; // 再访问根节点并输出
	trav_in(now->rson);  // 再访问右子树
}

非递归遍历

• 非递归遍历的思想要比递归法复杂，但效率可能略高于递归遍历。
• 递归函数之所以能便捷地实现遍历，事实上是因为隐含了栈的结构。因此非递归算法需要手动实现栈。
• 前序遍历的实现思路如下：
  • 创建一个栈，并将根节点入栈。
  • 循环执行以下操作，直到栈为空：
    • 弹出栈顶元素，并访问它。
    • 如果该节点有右子树，则将右子树入栈。先右后左，这样在之后的循环访问时才能先左后右地访问。
    • 如果该节点有左子树，则将左子树入栈。
• 中序遍历相对前序遍历复杂一点。① 由于总是需要先访问左子树，为了保证对于每一个子树的遍历都是中序的，那就需要一路访问左子树的左子树的……左子树，即最左的子树。② 把上述所有的节点按顺序放进栈里面，然后取出最顶上那个来访问。③ 接着就需要访问当前节点的右子树了。由于对于右子节点也需要执行上述的完整操作，因此放到下一次循环来访问。这时就需要一个指针来指示每一次循环从哪里开始（即当前根节点）。实现思路如下：
  • 创建一个栈和一个指针p，初始时指向根节点。
  • 循环执行以下操作，直到栈为空：
    • 将指针p指向左子树的最左节点，并将路径上的所有节点入栈。
    • 弹出栈顶元素，并访问它。
    • 将指针p指向栈顶元素的右子树。
• 后序遍历更加复杂一点。因为根节点最后访问，不妨再开一个栈，把当前节点压入栈中，那么最后输出时把栈中内容挨个输出，就是后序的遍历序列了。需要注意的是左右子树访问的顺序。因为实际上倒了两次栈，所以还是先左后右。实现思路如下：
  • 创建两个栈s1和s2，并将根节点入栈s1。
  • 循环执行以下操作，直到栈s1为空：
    • 弹出栈顶元素，并将它入栈s2。
    • 如果该节点有左子树，则将左子树入栈s1。
    • 如果该节点有右子树，则将右子树入栈s1。
  • 弹出栈s2中的所有元素，即为后序遍历的结果。
• 以下是这三种遍历非递归算法的参考代码。

void trav_pri_norec(Node *root) // 前序遍历
{
	stack<Node*> s; // 定义一个栈，用于存放遍历的节点
	s.push(root); // 将根节点压入栈中
	while (!s.empty())
	{
		Node* node = s.top();s.pop(); // 取出栈顶节点
		cout << node->dat << " "; // 输出节点值
		// 将右子节点压入栈中
		if (node->rson->dat != '#')
			s.push(node->rson);
		// 将左子节点压入栈中
		if (node->lson->dat != '#')
			s.push(node->lson);
	}
}
void trav_in_norec(Node *root) // 中序遍历
{
	stack<Node*> s; // 定义一个栈，用于存放遍历的节点
	Node* node = root; // 定义一个指针，指向当前遍历的节点
	while (node->dat != '#' || !s.empty())
	{
		// 将左子树中的所有节点压入栈中
		while (node->dat != '#')
		{
			s.push(node);
			node = node->lson;
		}
		// 取出栈顶节点，输出节点值
		node = s.top(); s.pop();
		cout << node->dat << " ";
		// 遍历右子树
		node = node->rson;
	}
}
void trav_post_norec(Node *root) // 后序遍历
{
	stack<Node*> s1, s2; // 定义两个栈，s1用于存放遍历的节点，s2用于存放输出结果
	s1.push(root); // 将根节点压入s1中
	while (!s1.empty())
	{
		Node* node = s1.top(); // 取出s1的栈顶节点
		s1.pop(); // 弹出s1的栈顶节点
		s2.push(node); // 将该节点压入s2中
		// 将左子节点和右子节点分别压入s1中
		if (node->lson->dat != '#')
			s1.push(node->lson);
		if (node->rson->dat != '#')
			s1.push(node->rson);
	}
	// 输出遍历结果
	while (!s2.empty())
	{
		Node* node = s2.top();
		s2.pop();
		cout << node->dat << " ";
	}
}