小批量梯度下降入门案例 —— 构造一元一次方程拟合模型

简介

梯度下降

梯度下降是一种优化算法，用于最小化一个函数，通常是在机器学习和人工智能中用来最小化损失函数，从而找到模型参数的最佳值。
常见的梯度下降算法主要有三种变体：

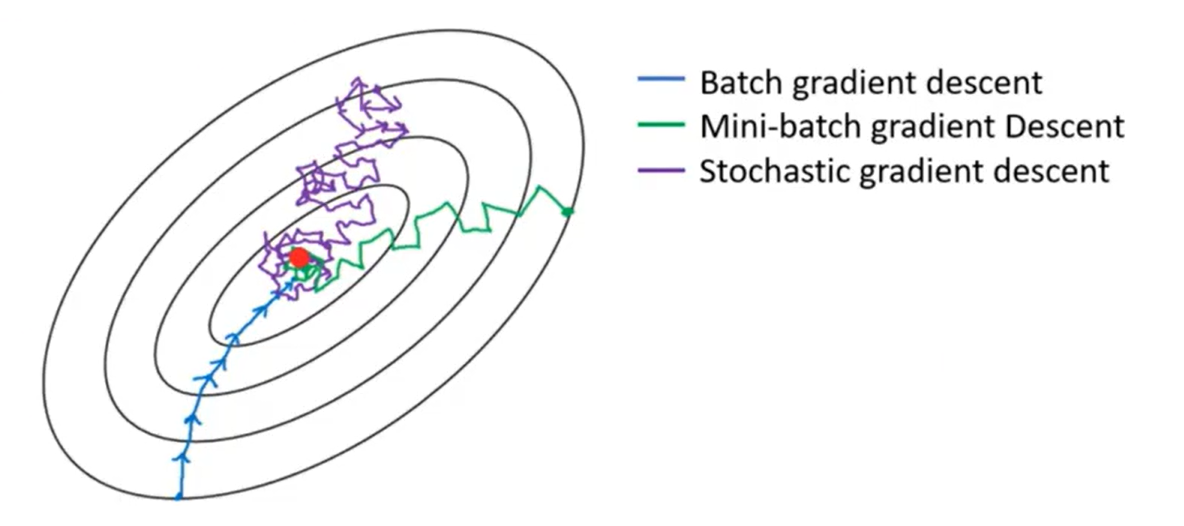
• 批量梯度下降（Batch Gradient Descent, BGD）：每次迭代使用整个数据集来计算梯度。
• 随机梯度下降（Stochastic Gradient Descent, SGD）：每次迭代只使用一个数据点来计算梯度。
• 小批量梯度下降（Mini-batch Gradient Descent, MBGD）：每次迭代使用一小部分数据点来计算梯度，介于BGD和SGD之间。

三种梯度下降的收敛曲线：

为什么选择小批量梯度下降？

梯度计算公式：

\[\nabla_{\boldsymbol{\Theta}} L(\boldsymbol{\Theta}) = -\frac{1}{n} \mathbf{X}^\top (\mathbf{X\Theta - y}) \]

其中：

• \(\nabla_{\boldsymbol{\Theta}} L(\boldsymbol{\Theta})\)：表示损失函数 ( L ) 对参数矩阵 \(\boldsymbol{\Theta}\) 的梯度。
• \(n\)：是数据集中样本的总数。
• \(\mathbf{X}\)：是一个 \(n \times m\) 的特征矩阵，其中 \(m\) 是特征的数量。
• \(\boldsymbol{\Theta}\)：是一个 \(m \times 1\) 的参数矩阵。
• \(\mathbf{y}\)：是一个 \(n \times 1\) 的向量，包含 \(n\) 个样本的目标值。

此算法时间复杂度随样本数量 \(n\) 的增长级别是 \(n^2\)。

现实生活中，样本数量往往达到 \(10^3\) 数量级以上，若使用BGD算法，将面临收敛速度慢、计算成本高等问题。而SGD在每次迭代中只使用一个样本来计算梯度，这导致梯度估计具有很高的方差和噪声。因此，更新步骤可能会受到单个样本特性的影响，导致参数更新方向不稳定。

MBGD将样本划分为多个批次，分批进行处理，以此保证一定的算法稳定性的同时，获取更快的收敛速度，减小计算成本。

本案例中，随机生成了一个带截距的一元一次方程和若干组随机数据，使用numpy操作矩阵，梯度下降公式训练模型，matplotlib对源数据和模型可视化。

运行截图

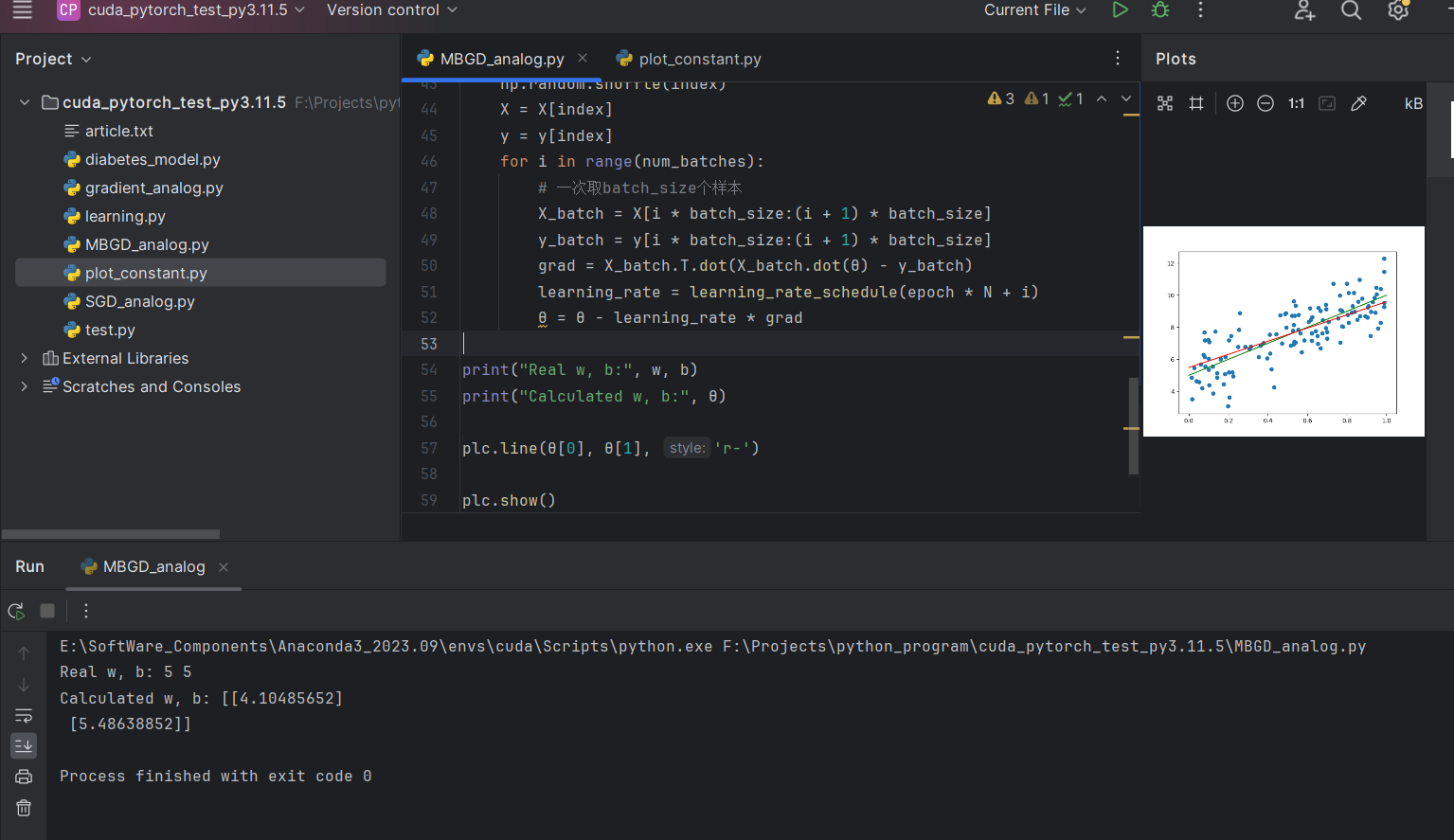
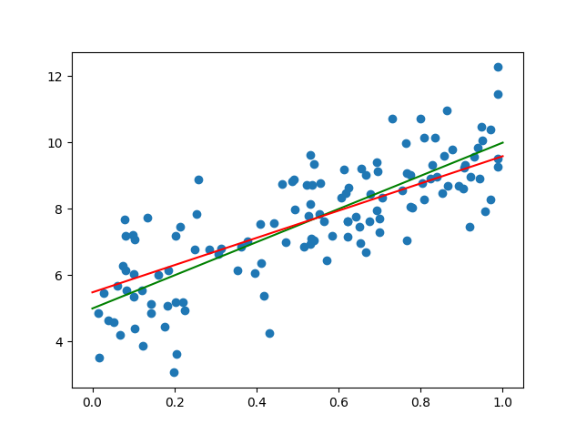
绿线：标准答案直线
红线：模型拟合生成的直线

Full Code

MBGD_analog.py

import matplotlib.pyplot as plt
import numpy as np
import plot_constant as plc

'''
小批量梯度下降（Mini-Batch Gradient Descent, MBGD）
'''

# 样本数，特征个数（引入偏置之前）
N, M = 128, 1

# 1.创建数据集X，y
X = np.random.rand(N, M)
w, b = np.random.randint(1, 10, size=2)
# 为y添加噪声
y = w * X + b + np.random.randn(N, M)

# 2. 绘制预设的回归线和点
plc.dots(X, y)
plc.line(w, b, 'g-')

# 3.在X中引入偏置项
X = np.concatenate((X, np.ones((N, 1))), axis=1)

# 4.学习率调整函数
t0, t1 = 5, 500
def learning_rate_schedule(t):
    return t0 / (t + t1)


# 5.创建超参数轮次、样本数量、小批量数量
epochs = 100
batch_size = 16
num_batches = int(N / batch_size)

# 6.初始化W0...Wn，标准正态分布
θ = np.random.randn(M + 1, 1)

# 7.多次循环实现梯度下降，最终结果收敛
for epoch in range(epochs):
    # 每个轮次开始分批迭代前打乱索引顺序
    index = np.arange(N)
    np.random.shuffle(index)
    X = X[index]
    y = y[index]
    for i in range(num_batches):
        # 一次取batch_size个样本
        X_batch = X[i * batch_size:(i + 1) * batch_size]
        y_batch = y[i * batch_size:(i + 1) * batch_size]
        grad = X_batch.T.dot(X_batch.dot(θ) - y_batch)
        learning_rate = learning_rate_schedule(epoch * N + i)
        θ = θ - learning_rate * grad

print("Real w, b:", w, b)
print("Calculated w, b:", θ)

plc.line(θ[0], θ[1], 'r-')

plc.show()

plot_constant.py

import matplotlib.pyplot as plt
import numpy as np


def dots(X, y):
    plt.scatter(X, y)


def line(w, b, style):
    x_line = np.linspace(0, 1, 10)  # 生成从0到1的10个点
    y_line = w * x_line + b  # 根据线性方程计算y值
    # 绘制直线
    plt.plot(x_line, y_line, style, label='Linear function: y = wx + b')


def show():
    plt.show()