(转载) 浅谈高斯过程回归

 

网上讲高斯过程回归的文章很少，且往往从高斯过程讲起，我比较不以为然：高斯过程回归（GPR）， 终究是个离散的事情，用连续的高斯过程( GP) 来阐述，简直是杀鸡用牛刀。所以我们这次直接从离散的问题搞起，然后把高斯过程逆推出来。

 

这篇博客有两个彩蛋，一个是揭示了高斯过程回归和Ridge回归的联系，另一个是介绍了贝叶斯优化具体是怎么搞的。后者其实值得单独写一篇博客，我在这里就是做一个简单介绍好了，但没准就不写了，想想就累。

高斯过程回归 的 Intuition

　　假设有一个未知的函数f  : R–> R ，

　　在训练集中，我们有3个点 x_1, x_2, x_3,   以及这3个点对应的结果，f1,f2,f3. (如图) 这三个返回值可以有噪声，也可以没有。我们先假设没有。

　　so far so good. 没什么惊讶的事情。

　　高斯过程回归的关键假设是：

给定 一些  X 的值，我们对  Y 建模，并假设 对应的这些 Y 值 服从 联合正态分布！

（更正式的定义后面会说到）

　　换言之，对于上面的例子，我们的假设是：

　　一般来说，这个联合正态分布的均值向量不用操心，假设成0 就蛮好。（讲到后面你就知道为什么了）

　　所以关键是，这个模型的 协方差矩阵K 从哪儿来。

　　为了解答这个问题，我们进行了另一个重要假设：

　　如果两个x 比较相似（eg, 离得比较近），那么对应的y值的相关性也就较高。换言之，协方差矩阵是 X 的函数。（而不是y的函数）

　　具体而言，对于上面的例子，由于x3和x2离得比较近，所以我们假设 f3和f2 的correlation 要比 f3和f1的correlation 高。　　

　　话句话说，我们可以假设协方差矩阵的每个元素为对应的两个x值的一个相似性度量：

那么问题来了，这个相似性怎么算？如何保证这个相似性度量所产生的矩阵是一个合法的协方差矩阵？ 

好，现在不要往下看了，你自己想3分钟。你也能想出来的。 提示：合法的协方差矩阵就是 (symmetric) Positive Semi-definite Matrix （。。。。。。。。。。。。思考中） 好了时间到。

　　答案： Kernel functions !

　　矩阵A正定是指,对任意的X≠0恒有X^TAX＞0。
　　矩阵A半正定是指,对任意的X≠0恒有X^TAX≥0。

　　判定A是半正定矩阵的充要条件是：A的所有顺序主子式大于或等于零。

　　如果你了解SVM的话，就会接触过一个著名的Mercer Theorem，（当然如果你了解泛函分析的话也会接触过 ），这个M定理是在说：一个矩阵是Positive Semi-definite Matrix当且仅当该矩阵是一个Mercer Kernel .

　　所以我们在svm里用过的任何Kernel都能拿过来用！

　　举个栗子，在高斯过程回归里，一种非常常见的Kernel就是SVM里面著名的高斯核（但是为了让命名不是那么混淆，文献中一般把这个Kernel称作 squared exponential kernel.

　　具体而言就是

　回归分析

　　好了，现在可以做回归分析了：

　　如果我们现在又有了一个新的点 x*

　　这个新的点对应的f* 怎么求？（如下图）

根据假设，我们假设 f* 和 训练集里的  f1, f2, f3 同属于一个 （4维的）联合正态分布！

也就是说，不仅 f1,f2,f3属于 一个3 维的联合正态分布（参数可以算出来），而且 f* 和 f1,f2,f3属于（另一个）4维的联合正态分布，用数学的语言来表达就是：

　　首先我们来看一看，这个4 x 4 的 矩阵能不能算出来：

黄色的大K，是依据训练集的3维联合分布算出来的，绿色的K*, 是测试点x* 分别和每一个训练集的x 求出来的。所以整个联合分布我们都知道了。

　　接下来的事情就好办了，我们既然已经知道（f,f*)的联合分布P(f, f*)的所有参数, 如何求p(f*) ？好消息是这个联合分布是正态的，我们直接用公式就能搞出来下面的结果（using the marginalization  property）：

　　不难求出f* 隶属于一个1维的正态分布， 参数是：

　　所以这是一种贝叶斯方法，和OLS回归不同，这个方法给出了预测值所隶属的整个（后验）概率分布的。再强调一下，我们得到的是f* 的整个分布！不是一个点估计，而是整个分布啊同志们。

 In addition, 不仅可以得到  f*这一个点的分布，我们对这个未知的 函数 也可以进行推断！换言之，如果把一个函数想成一个变量，那么高斯过程回归可以求出这个函数的分布来。(distribution over functions)不幸的是，我们的计算机只能存储离散的数据，怎么表示一个连续的函数呢？

　　好办，我们对一个区间里面均匀地硬造出来1万个测试点x*, 然后求出这些测试点和训练集所对应的y（一个巨高维的向量）的联合分布，然后在这个巨高维的联合分布里采样一次，就得到了函数的（近似的）一个样本。

　　比如训练集就三个点，测试集1万个x，图中的每一个红点就分别是这些点f* 的均值，（当点很多的时候，就可以假设是一个“连续”的函数了）而蓝色的线代表一个或两个标准差的bound.

　　我们如果从这个分布中采样10次，就可以得到10个巨高维的向量，也就是从这个后验概率中sample出来的10个函数的sample.  plot出来长这个样子：

　　含有已知数据（训练集）的地方，这些函数都离的很近（variance很低），没有数据的时候，这个spread就比较大。

　　也许你会问：我为毛要搞出来函数的分布？我为毛要关心这个variance. 在很多问题中，我们不仅仅需要知道预测值的点估计，而且要知道这个估计有多少信心在里面（这也是贝叶斯方法的好处之一）

举个例子：Multiple Bandit Problem假设 我们已经有了几个油井，每个油井的价值不一样，我们在这个二维平面上，利用高斯过程回归，对每一个地理位置估计一个该位置对应的出油量。而开发每一口井是有成本的，在预算有限的情况下，如果想尽可能少地花钱，我们就需要定义一个效益函数，同高斯过程回归的预测结果相结合，来指导我们下一次在哪儿打井。这个效益函数往往是 预测值 和  方差 的一个函数。以上这个例子，就是高斯过程回归在贝叶斯优化中的一个典型应用。有时间专门写一篇。

高斯过程

好了，现在终于可以讲一讲高斯过程了。

高斯过程是在函数上的正态分布。（Gaussian distribution over functions)具体而言就是

　　我们具体用的时候，模型假设是酱紫的：

　　我们观察到一个训练集 D

　　给定一个测试集 X*  （ X* 是一个 N* x D 的矩阵， D是每一个点的维度）我们希望得到 一个 N* 维的预测向量 f*. 高斯过程回归的模型假设是

　　然后根据贝叶斯回归的方法，我们可以求出来 f*的后验概率：

　　This is it. 要啥有啥了。

有噪声的高斯过程

　　下面着重说一下有噪声情况下的结果，以及此情况下和Ridge Regression的神秘联系。

当观测点有噪声时候，即， y = f(x) + noise, where noise ~N(0, sigma^2)

我们有

　　发现没，唯一区别就是 K 变成 了 Ky，也就是多加了一个sigma。

　　这个很像是一种regularization. 确实如此。

• 好了，下面就说说这个 GPR的  insight，这个模型到底想干什么

　　如果只有一个测试点，那么输出的f* 就是隶属于一个1维的正态分布了，具体而言：

　　再看，我们回想一下Ridge Regression （小编注：下图argmax应为argmin）

　　我们仔细观察一下上面那个蓝色的框框

　　所以说，ridge回归是一种最最最最简单的高斯过程回归，核函数就是简单的点积！

而高斯过程的核函数可以有很多，除了上面提到的squared exponential, 有整整一本书都在讲各种kernel和对应的随机过程

　　所以高斯过程是一个非常包罗万象的根基，类似于小无相功。

 　　高斯过程回归(GPR)和贝叶斯线性回归类似，区别在于高斯过程回归中用核函数代替了贝叶斯线性回归中的基函数（其实也是核函数，线性核）。

　　来看看多维高斯分布的一些重要性质，第一个性质为两个相互独立的多维高斯分布A和B的和也是一个多维高斯分布C，且C的均值和方差都为A和B均值方差的和。第二个性质为：两个多维高斯分布之和构成的分布C而言，在已知一部分观察值C1的条件下，另一部分观察值C2的概率分布是一个多维高斯分布，且可以用A和B中对应的信息来表示。

如下：

　　 　　

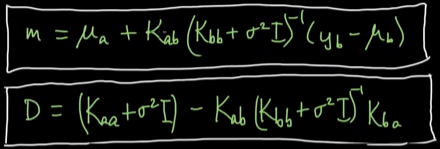
　　由贝叶斯线性回归和高斯过程回归的对比可知，贝叶斯线性回归是高斯过程回归中的一个子集，只是它用的是线性核而已，通过两者的公式就可以看出它们之间的关系：

 　　

　　上面是贝叶斯线性回归，下面是高斯过程回归。

　　简单例子：

　　假设现在已经观察到了6个样本点，x为样本点特征（一维的），y为样本输出值。现在新来了一个样本点，要求是用高斯回归过程来预测新来样本点的输出值。这些样本点显示如下;

 　　

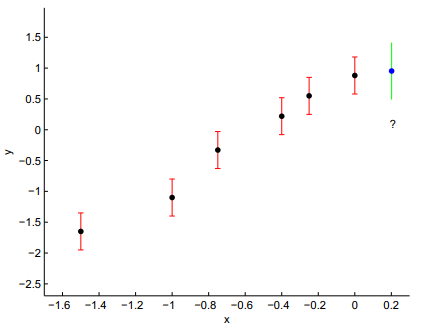
　　其中前面6个点是已知输出值的训练样本，其值为：

　　第7个点是需要预测的样本，红色的垂直条形线表示观察输出值的误差，绿色的垂直条形线为用高斯过程回归的误差。

　　用GPR解该问题的流程大概如下（对应前面讲的一些基础知识）：

　　1. 选择适当的u（均值函数）和k（核函数），以及噪声变量σ，其中核函数的选择尤其重要，因为它体现了需处理问题的先验知识，应根据不同的应用而选择不同的核。

　　2. 计算出训练样本的核矩阵（6*6），如下：

 　　

　　3. 计算需预测的点  与训练样本6个点的核值向量，如下：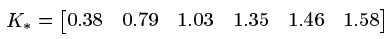

　　4. 自己和自己的核值为 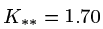 且此时整个样本的多维高斯分布表达式为：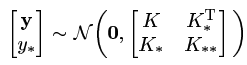 

　　5. 通过前面m和D的公式，求得m=0.95，D=0.21.

　　6. 画出最终结果如下：

　　

　　这个例子来源于论文Gaussian Processes for Regression A Quick Introduction中，它的核函数等参数选择和基础知识部分的不同，但这里主要是对GPR的应用有个简单的宏观上的理解，让大脑对GPR应用有个初步的印象，否则有了那么多的公式推导但不会应用又有什么用呢？

　　http://www.cnblogs.com/tornadomeet/archive/2013/06/14/3135380.html

　　http://dataunion.org/17089.html

　　http://www.cnblogs.com/tornadomeet/archive/2013/06/15/3137239.html