[CVPR2021] AttentiveNAS: Improving Neural Architecture Search via Attentive Sampling
1. 背景(Two-stage NAS)
该篇论文(AttentiveNAS)聚焦的是Two-stage NAS,比较出名的算法有 BigNAS,Once-for-all NAS (OFA), SPOS等等,不过他们都采用的uniform的采样去训练Supernet,即把所有的子网一视同仁,尽可能分配相等的采样机会。Two-stage NAS算法通常包含如下两个步骤:
1.1 Constraint-free pre-training
第一步是训练Supernet,数学化公式如下:
- 第一项是所有子网loss的期望,这些子网共享权重
- 第二项是对共享权重的约束
1.2 Resource-constrained searching
第二步是基于训练好的Supernet去评估子网络,然后选出Pareto-front模型。数学公式可表示成如下形式:
一般常用的搜索算法是进化算法或者Monte Carlo tree search算法。
2. AttentiveNAS
2.1 Mathematics
AttentiveNAS想做的是把两个步骤融合成一步,可表示成如下数学公式:
- 公式(1)中的表示候选网络的FLOPs,最优的简单理解就是 使得 不同FLOPs下() 所有子模型的loss期望 () 最小的解。
- 公式(2)和(3)都是分别使用Monte Carlo采样做近似计算。比如 表示将整个搜索空间划分成个FLOPs区间,表示每个FLOPs区间内每次采样更新的模型数量,是indicator函数,即如果模型结构满足指定条件,则等于1,反之为0。
2.2 Pseudo Algorithm

上面数学公式中提到的是一个指示函数,其条件是是否属于 best或worst Pareto-front,分别记为BestUp-k和WorstUp-k
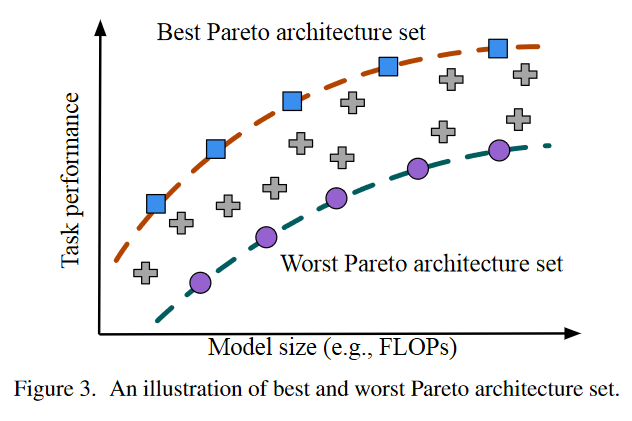
它的这种优化策略类似于BigNAS里的Sandwich策略,即把最好的和最差的都优化好了,那么就认为中间的也一定程度上被优化好了。
3. Experimental Results
训练好了Supernet,接下来就是去做实验验证这种训练方式的稳定性和有效性。
3.1 Prediction
对于任意一个子模型,我们可以得到它的评估性能(直接从Supernet中继承对应模块的权重)和真实性能(test acc),一般来说如果足够数量模型的评估性能和预测性能之间存在强相关性,则说明训练好的Supernet能够有效地知道后面对模型的搜索。
评估性能有两种策略可以获取:
-
- 基于训练好的Supernet去初始化自网络,然后在验证集上去评估模型性能;
-
- 上面的方法耗时比较长,所以另一种策略是训练一个预测器来预测每个模型的性能。本文的做法是先跑1024个子模型得到他们的真实性能,然后基于这1024个模型组成的数据对(模型结构编码,test acc)训练得到一个随机森林回归树。
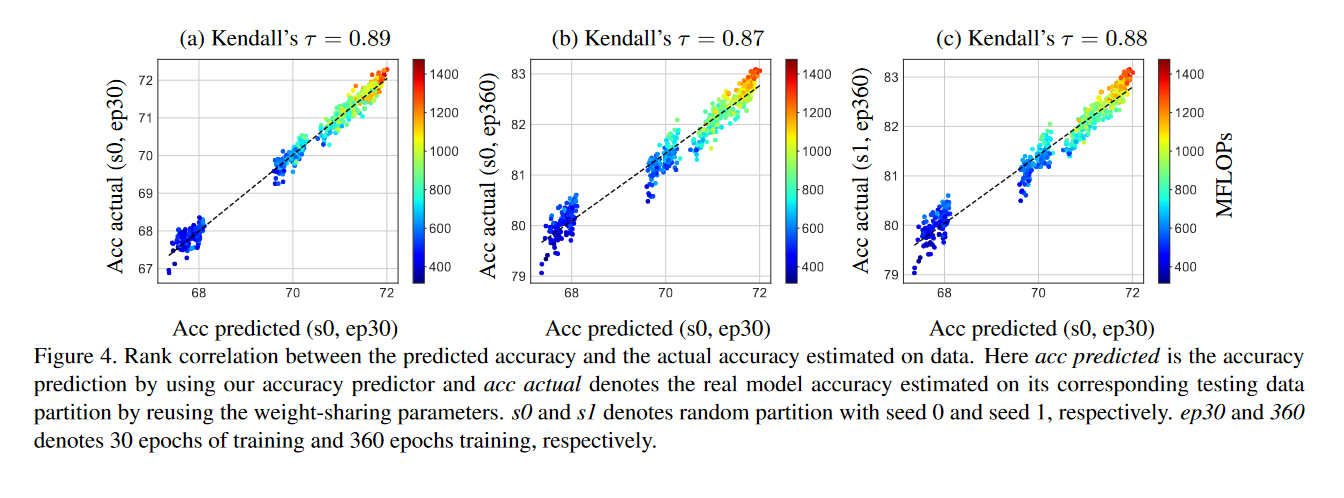
下图是AttentiveNAS基于第二种策略得到的实验结果, 其中分别表示在两个不同种子下跑的实验结果,ep30/ep360表示在训练30个epoch和360个epoch下的结果。可以看到预测的ACC和真实的ACC之间的相关系数Kendall tau(其范围是-1~1)还是比较大的。这表明预测器还是能有效预测出模型的ACC的。
3.2 Sampling Results

不同采样训练的结果如上图所示,BestUp-50表示从best Pareto front set中每个sampling step采样50个模型做评估。根据上面的结果可以观察到训练WorstUp要比BestUp效果更好,这个常规的想法不太一致。
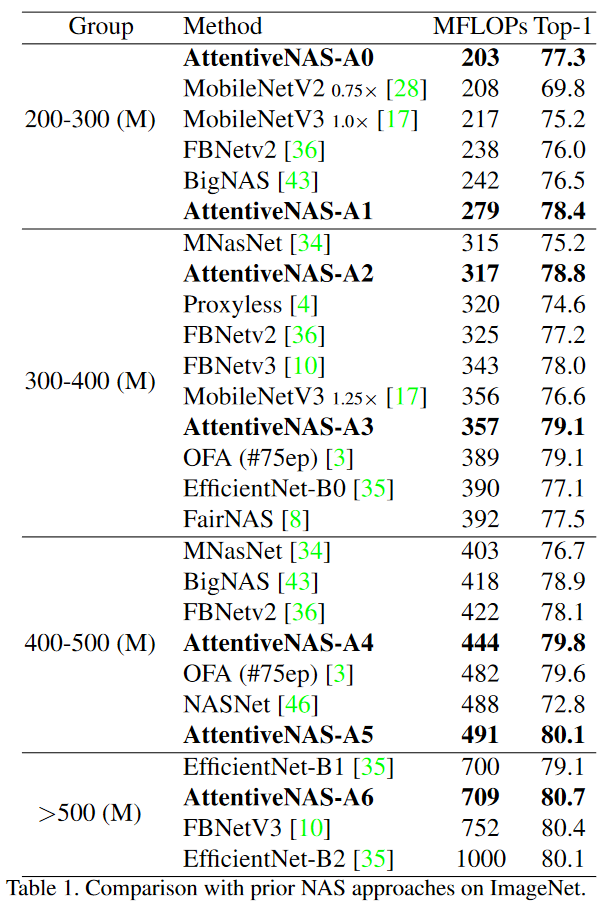
最终在ImageNet上的结果如下表所示



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
2020-04-26 【GAMES101-现代计算机图形学课程笔记】Lecture 05 Rasterization 2 (Antialiasing and Z-Buffering)
2020-04-26 【GAMES101-现代计算机图形学课程笔记】Lecture 05 Rasterization 1 (Triangles)