通过损失函数优化提高训练速度、准确性和数据利用率
论文: Improved Training Speed, Accuracy, and Data Utilization Through Loss Function Optimization
简介
该论文的主要贡献是提出了Genetic Loss-function Optimization (GLO) 框架来搜索新的损失函数。该框架可以分成层两个如下图示的两个阶段:
- 搜索loss函数的形式:比如
- 优化loss函数的系数:即优化上面例子中的
这三个系数,其中
分别表示真实和预测值。
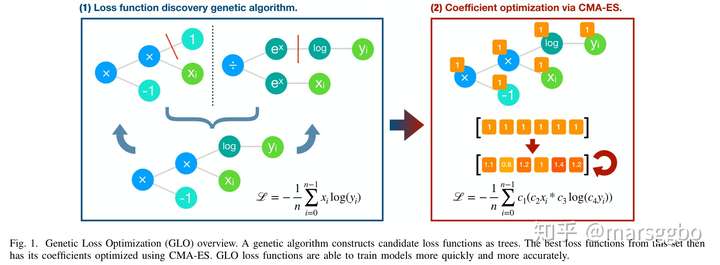
搜索损失函数
GLO使用population-based的进化搜索策略,损失函数被编码成树结构。树节点上的操作从如下的搜索空间总进行搜索:
- Unary operators:
- Binary operators:
- Leaf nodes:
, 其中
分别表示真实和预测值。
这三类操作的权重比例是: Unary : Binary : leaf= 3 : 2 : 1
搜索过程中出现如下情况的树,其fitness会被赋值为0
- 一颗树中不同时包含至少有一个x和y
- 模型训练过程中出现NaN
Crossover
树结构的crossover的方式是对于给定的两个parent trees, 分别随机选择一个节点作为crossover point。那么以crossover point作为根节点可以得到两个subtrees。那么crossover其实就是按照一定概率交换这两个subtrees, 论文中给出的概率是80%。
如下图示,上面两个是parent trees,红色直线截取位置的节点即为crossover point,在crossover之后即可得到下面的树结构。

Mutation
Mutation操作如下:

优化损失函数系数
搜索到损失函数表达式后,每个节点的系数都默认为1,如下图示。很显然需要优化系数数等于节点数,但是其实通过表达式简化可以减少需要优化的系数数,比如 ,原本需要优化3个系数,现在只需要优化一个了。具体的优化算法采用的是 协方差矩阵自适应进化算法(CMA-ES) [1],论文里对这个算法没有细节的介绍,建议看看这个博文,写的浅显易懂。
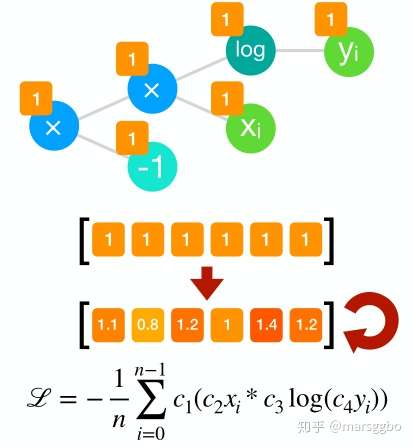
实验评估
论文中采用了MNIST和CIFAR-10作为测试数据集,并且将搜索到的损失函数命名为 Baikal,意思是贝加尔湖,文中的解释是因为它的形状像贝加尔湖hhh,函数表达式如下:
使用CMA-ES算法搜索到的系数如下:
其中
在MNIST数据集上的平均实验结果(10个模型)如下:
- Testing accuracy
| Loss function | Accuracy |
|---|---|
| Crossentropy | 0.9899 |
| Baikal | 0.9933 |
| BaikalCMA | 0.9947 |
- Training speed

- Training data requirements
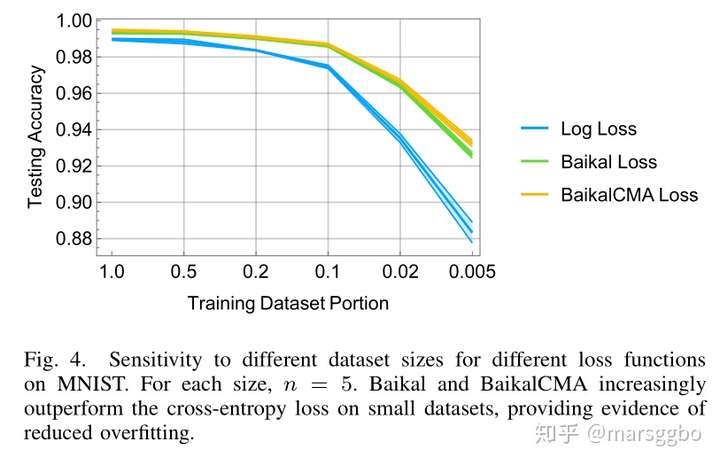
- 迁移至CIFAR-10的结果
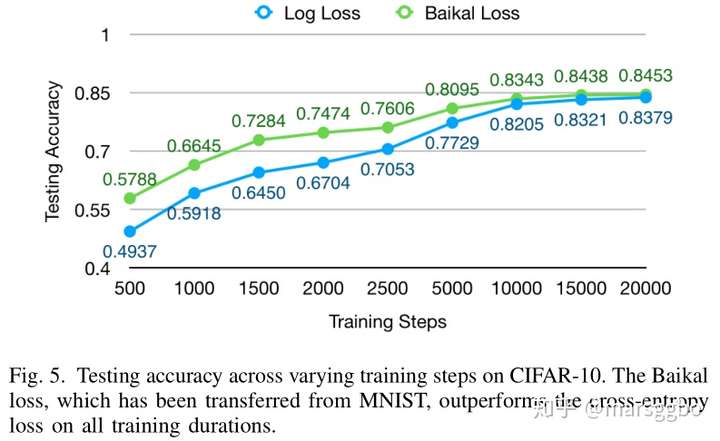
分析:为什么Baikal损失函数更优?
为了方便分析为什么Baikal损失函数效果更好,这里以二分类为例进行介绍
下图展示了时Baikal损失函数2D可视化,可以看到当预测值趋近于真实值(即1)的时候,交叉熵损失单调递减;而对于Baikal函数,当预测值非常接近于真实值的时候,loss值反而会上升,这可能有点反直觉,但是这样的好处时可以避免模型对自己的预测太过于自信,因此也可以理解成一种正则化。

参考文献
- [1] N. Hansen and A. Ostermeier, “Adapting arbitrary normal mutation distributions in evolution strategies: The covariance matrix adaptation,” in Proceedings of IEEE international conference on evolutionary computation.IEEE, 1996, pp. 312–317.
微信公众号:AutoML机器学习

MARSGGBO♥原创
如有意合作或学术讨论欢迎私戳联系~
邮箱:marsggbo@foxmail.com
2020-11-18 09:03:50


