【GAMES101-现代计算机图形学课程笔记】Lecture 10 Geometry 1 (介绍)
之前的课程里介绍了
- Shading 1 & 2
- Blinn-Phong reflectance model
- Shading models / frequencies
- Graphics Pipeline
- Texture mapping
- Shading 3
- Barycentric coordinates
- Texture antialiasing (MIPMAP)
- Applications of textures(本节会补充介绍)
(补充 1)Shading - applications of textures
因为上一节还有一丢丢纹理相关的内容没讲完,所以在这一节补充。
在介绍纹理的应用之前,首先还是给纹理做一个大致的概述:
- 在现代GPU中, texture=memory + range query (Filtering),即纹理其实就是存储在GPU上的一块内存上的数据,然后我们可以对这块内存做区域查询(例如MipMap)。
常用的纹理应用有如下:
- Environment lighting (环境光)
- Store microgeometry
- Procedural textures
- Solid modeling
- Volume rendering
1.1 如何表示环境光
如下图示,通常一个光滑的表面(比如水晶球)会反射环境光,因此我们可以看到球面上会被映射出其他物体。那么计算机中如何表示这个呢?

一种方法是Spherical Environment Map,即先把环境光信息记录在球面上,其中还包括了球面与二维平面之间的映射关系。

但是上面这种方法会有一个问题,即映射到二维平面后会导致扭曲,如下图示:

既然球面会导致扭曲,那么一种改进的思路如下,即我们不再把信息记录在球上,而是记录在一个立方体的表面上,这个立方体会包住原来的球体。
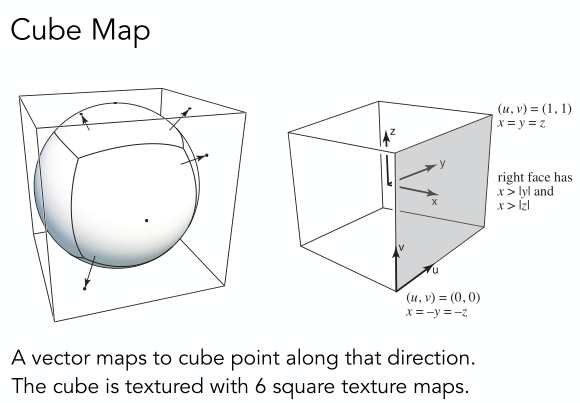
1.2 凹凸贴图(法线贴图)
我们可以看到下图的橘子会有坑坑洼洼的感觉,那这种效果如何实现呢?-- 一种方式是构造出一种复杂的形状来显示出凹凸感,但是这样实现起来会比较复杂;
- 另一种方式就是通过法线贴图来实现,这种方法的一个大致的思路是比如纹理全部是橘色的,只不过在映射到二维平面时,我们会调整每个纹理的法向。前面我们有介绍过法线方向的改变会导致光的亮度等变换,这样就等同于像素之间有了明暗变化,所以就有了凹凸感。

上面提到的法线贴图方法并不需要改变任何几何信息,即不需要增加二维平面划分成更多的三角形。那具体是怎么实现的呢?这需要用到Bump Mapping技术。
总结起来,Bump Mapping其实就是对每个像素的平面法向做了扰动。如下图示,黑色曲线表示真实的物体光滑表面,而黄色曲线则是扰动后的效果。我们可以看到原来的P点的法向经过扰动后发生了改变,这样就可以实现法线贴图。那么扰动后的法向如何计算呢?
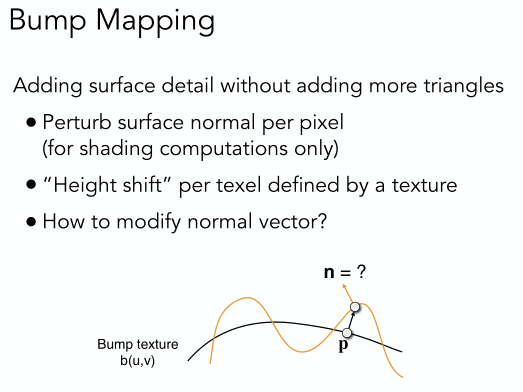
1.2.1 flatland case
首先看一下在一维情况(flatland case)下如何计算,假设下图中的点为P点。
- P点原始的法线方向是朝上的,即\(n(p)=(0,1)\)。
- 下图中的蓝色曲线表示法线贴图,那么P点横向移动一个单位后,向上则会移动\(\mathrm{dp}\),(假设P点会朝着切线方向运动)。切线方向即为该点的梯度,由梯度计算公式可知\(\mathrm{dp}=\mathrm{c}^{\star}[\mathrm{h}(\mathrm{p}+1)-\mathrm{h}(\mathrm{p})]\),其中\(c\)为一个常量,所以切线可表示为\((1,\mathrm{dp})\)。
- 既然知道了切线方向,那么法线方向就很容易计算出来了,即切线方向逆时针旋转90°即可,所以扰动后的法线方向为\(n(p)=(-dp,1).\text{normalized()}\)

1.2.2 3D case
同理在3D情况下则有两个方向的变换,即u,v方向。
需要注意的是flatland和3D这两种情况下我们都假设某点的法向是朝上的,所以说这个假设的法线方向其实是基于一个局部的坐标构建的,但是显然实际情况不是这样的。

1.2.4 Displacement mapping (位移贴图)
上述方法其实是通过对法线方向扰动实现凹凸效果,还有一种方法是位移贴图。
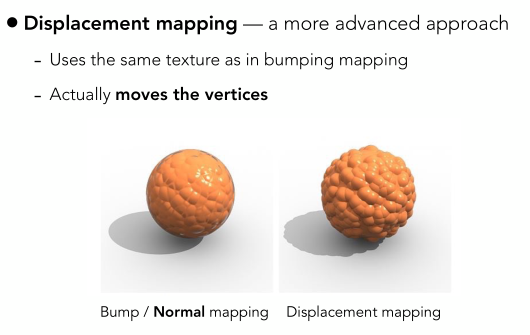
位移贴图和法线贴图使用的纹理是一样的,只不过位移贴图不再变换法线方向,而是真实地对每个三角形的顶点做一定的位移。上图中可以看出两种方法的区别(虽然右边看起来有点恶心。。):
- 左边的是法线贴图,可以看到它并没有改变物体形状(还是圆形),另外影子投影结果也是一个光滑球体的投影,所以这种方法其实是一种假象,欺骗了人的眼睛。
- 右边是位移贴图,可以看到凹凸感很明显,而且投影也体现出了这种凹凸感,比如凸起部位的投影也都显示出来了。
上面的对比可以看出位移贴图虽然效果更好,因为他需要对把物体划分成更多的三角形,即物体需要被划分的更加细致,这样才能更准确地描述出凹凸特点,但是它的计算量也是更大的。
所以一种权衡的方式就是将二者结合起来,即首先用法线贴图构建出一个比较粗糙的效果,然后基于这个粗糙结果,将每个三角形划分的更加小。这个在windows的DirectX库中有提供。
1.3 三维纹理
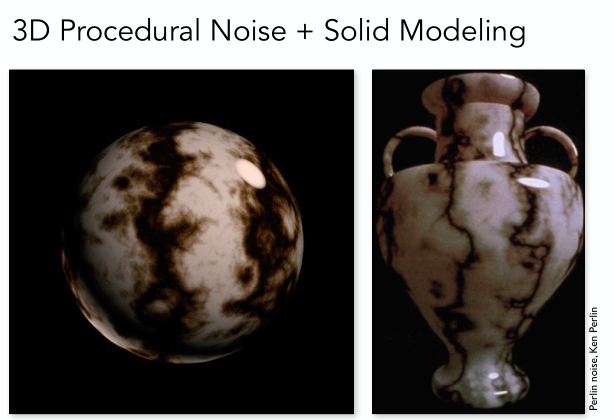
上面介绍的纹理应用都是应用在二维平面的,那么很自然就有三维的纹理应用。三维纹理的意思就是除了物体表面有纹理,物体内部也是有纹理的,而内部的纹理通常是通过生成某种三维噪声然后再做处理得到的。比如下图示展示的Perlin noise(柏林噪声),就可以得到一种大理石纹理的效果。
还有一种三维纹理的应用时医学上的应用,即volume rendering(体渲染)

2. Introduction of geometry
下面正式开始介绍几何,首先看几个例子(右下角是亮点哈哈哈):

下图给出了许多种表示几何的方式,大体上分为显式和隐式两种方法。
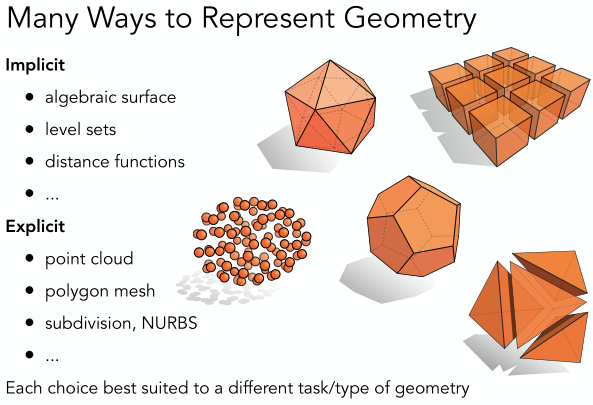
2.1 Implicit representations of geometry
我们首先看一下什么是隐式表示。隐式表示的意思是我不会告诉你具体某个部位长什么样子,相反我只会告诉你这个部位的点之间服从某种的关系,因此我们可以可以通过这种关系来构建几何。
举例来说,我们知道3D中一个球的表面上任意点坐标都满足\(x^{2}+y^{2}+z^{2}=1\)。
更通用地表达式是\(f(x,y,z)=0\),只要满足这个公式则表示该点在这个隐式定义的物体表面上,这也是隐式表示的一个优点。

当然,隐式表示也有一个很明显的缺点,即我们根据表达式不能直观地知道具体表示什么形状。比如下面的隐式表达式,如果只看式子我们根本不可能知道对应的物体的几何形状是什么。

- 其他有趣的式子:

- 隐式的还有一种常用的方法是constructive solid geometry(CSG),即对3D物体几何做布尔操作,看下面的例子:

- 符号距离函数(Signed Distance Function, SDF)
还有一种隐式表示的方式是符号距离函数,这部分内容看视频看了三遍,查了资料才明白什么意思,主要是感觉老师举的例子并不好帮助理解,泪奔~~o(>_<)o ~~。。。
首先介绍一下这个距离函数的“距离”是什么意思,我就是被这个搞的云里雾里的。
距离函数的意思是会返回当前点与任意物体表面的最短距离,如果返回的距离是负数,说明这个点在物体内部;如果为正,则在物体外部。以下图为例,蓝色圆圈表示以当前点离任意表面的最短距离作为半径得到的圆。可以看到每次求得一个半径后,会朝着指定方向移动这个半径的距离,进而计算下一次的半径,这样可以减少距离比较的次数。

知道是什么“距离”后我们就可以利用距离函数来构造各种几何形状了。如下图示(从左往右看),最开始是由两个球,我们知道每个球都对应了一个距离函数,假设为\(d_1,d_2\)。你可能对这个距离函数还是不太理解,我们再进一步解释,以\(d_1\)为例,假设最左边上面那个球的中心坐标是\((x_1,y_1,z_1)\),半径为\(r\),那么\(d_1=(x-x_1)^2+(x-x_1)^2+(x-x_1)^2-r^2=0\)。
那么我们只要将两个距离函数做一个融合(blending),随着融合程度的调整,我们可以得到右边一系列的几何图形,给人一种两个水滴合在一起的感觉。
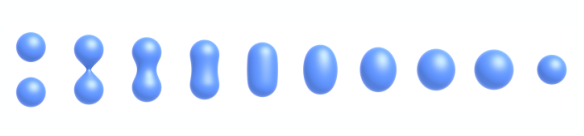
- level set methods
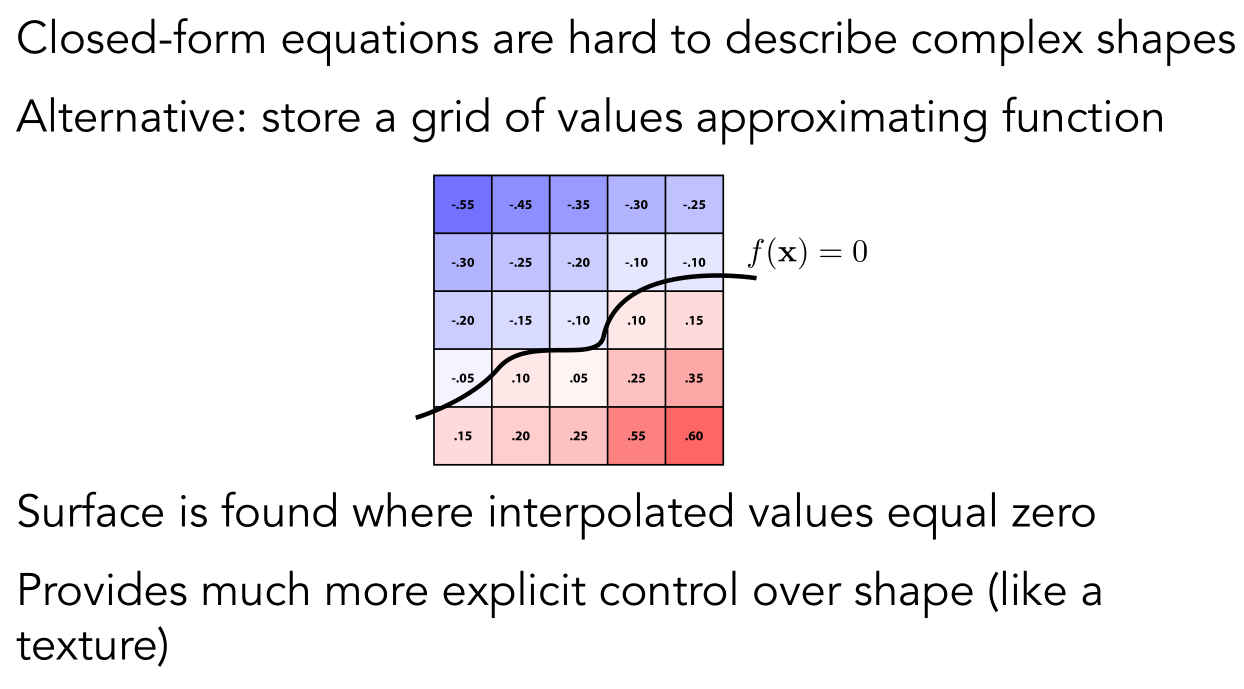
上面的距离函数需要定义出一个解析表达式,但是有时候我们不一定能够求出这个解析式。那么针对这种情况我们可以用level set(水平集)来表示几何形状。
我们看下面的例子来解释什么是level set。其实就是我们给每个格子设定一个值,然后找出值为的地方连起来就得到了level set,连接起来也就形成物体表面。
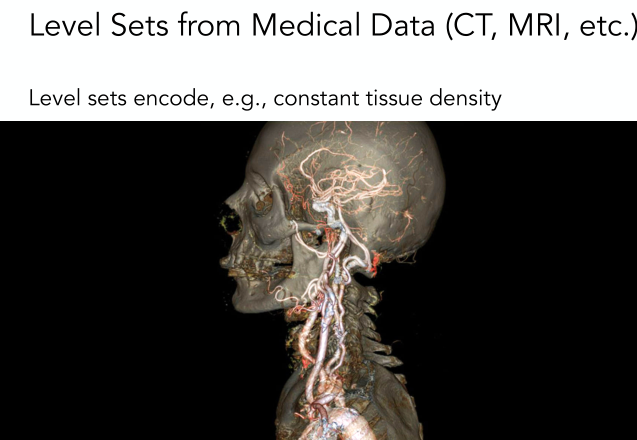
上面例子是在2D平面的levelset,我们也可以在3D上生成level set,这在医学数据上用的比较多。此时的一个大致思路是我们给三维定义出一个密度level set,因为不同器官组织的密度是不一样的,那么我们通过选取不同的levelset,也就得到了不同的器官或组织的表面形状了。
- fractals(分形)
还有一种表示方式是分形,现实生活中像雪花就是一种分形。比如它整体看起来是个六边形,然后我们细看每条边又是一个六边形。其他例子如下图示:

2.2 Explicit representations of geometry
另外一种表示方式则是显式表示。如下图示,我们会构建一个映射函数,这个函数会将左边的二维的平面图的每个点都映射到右边的三维几何图上。

还是用上面的例子来解释显式表示,可以看到这里的映射函数是
这里和上面的\(f(x,y,z)=0\)不一样,因为这里我们是直接将二维uv坐边上的某个点的左边通过某种映射关系直接映射到三维某个具体的坐标点了,所以这是显示的。我们只需要对二维平面上所有点遍历一遍即可得到映射后的几何形状,而前面介绍的隐式方法则需要我们根据等式来判断而为上的某个点是否在映射后的几何物体表面。这个区别需要区分开来。
很自然地,显式的缺点对应着隐式的优点,即判断一个点在物体表面内部或者外部就变得麻烦一些了。

2.3 表示方式总结
| 方法 | 优点 | 缺点 |
|---|---|---|
| 显式表示 | 很容易计算出每个点映射位置,直接得到映射物体的几何形状 | 不能直接判断某个点是在映射物体的内部还是外部 |
| 隐式表示 | 无法直接知道映射后的物体的几何形状 | 很容易判断二维某个点在映射后是在物体的内部还是外部 |
由上表可以知道目前还没有一种最优的表示方式,只能依靠需求来选择合适的方法。

