【GAMES101-现代计算机图形学课程笔记】Lecture 07 Shading 1 (Illumination, Shading and Graphics Pipeline)

本节内容摘要

• Visibility / occlusion （遮挡问题）
  • Z-buffering
• Shading （着色问题）
  • Illumination & Shading
  • Graphics Pipeline

1. 可见性问题

1.1 画家算法

真实世界中的物体之间相对于相机是有远近关系的，那么在2D平面上如何反应物体的先后关系呢？一个常用的方法是Painter's Algorithm (画家算法)，即先画远处的物体，然后把近处的物体画在远处物体的前面，如下图所示。

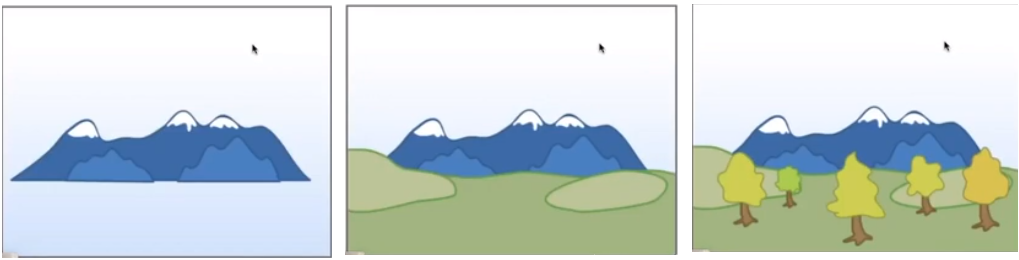
画家算法需要根据距离远近对不同物体进行排序，例如用快排的话，时间复杂度是\(O(nlogn)\)。这里的排序是植物体之间的远近关系比较好判断的情况，如果是下面这种情况，你说那个三角形在最前面呢？

所以一种常用的解决可见性问题的算法是Z-Buffer。

1.2 Z-Buffer

1.2.1 算法介绍

Z-Buffer的想法是不再对物体做远近排序，而是对每个像素做排序。

简单来说就是2D屏幕上的每个像素都记录两个缓存值，即最前面那张图的左下角为例（即地面）：

• 1）该像素所对应的3D物体的最小的Z轴坐标值，即对应地面的Z轴坐标。这个也叫做depth buffer 深度缓存，即存储每个像素点对应的深度信息。
• 2）对应Z轴坐标的3D物体的颜色信息，即地面的绿颜色。这个也叫作frame buffer，即存储每个像素点对应的颜色信息,这个buffer其实就是最后生成的图片。

之前的内容，我们始终假设相机位于原点，且朝着Z轴负方向，所以离相机越近，Z轴坐标绝对值越小，反之越大。这里为了方便起见（仅讨论深度问题），所以假设Z值永远是正数，即Z越小，表示越近；反之越远。

1.2.2 例子

下图给出了Z-Buffer的例子。可以看到离我们（相机）越近则表Z值越小，所以对应到右边的深度图，颜色也就越深。（0为黑色）

1.2.3 伪代码示例

Z-Buffer算法伪代码示例如下：

Initialize depth buffer to ∞
During rasterization:
	for (each triangle T)
		for (each sample (x,y,z) in T)
			if (z < zbuffer[x,y])  // closest sample so far
				framebuffer[x,y] = rgb; // update color
				zbuffer[x,y] = z;   // update depth
			else
				;  // do nothing, this sample is occluded

有一个问题需要注意，就是由于在计算机里，深度值一般都是由浮点数表示的，所以理论上来说3D物体的深度值是不会相等的 。但是当对深度值做近似处理的时候，比如取整，这个时候两个像素的深度值就一样了，那这个时候颜色信息选哪个像素点的呢？这是个好问题，不过闫老师说这个在后面的内容再介绍~

1.2.4 复杂度

Z-Buffer的复杂度是\(O(n)\)，注意这里只是找到最小值即可，所以只需遍历所有像素点。而前面提到的画家算法需要对不同物体做排序，所以即使用快排也得是\(O(nlogn)\)。

2. Shading （着色）

2.1 回顾

在介绍着色方法之前，先回顾一下前面学的内容。

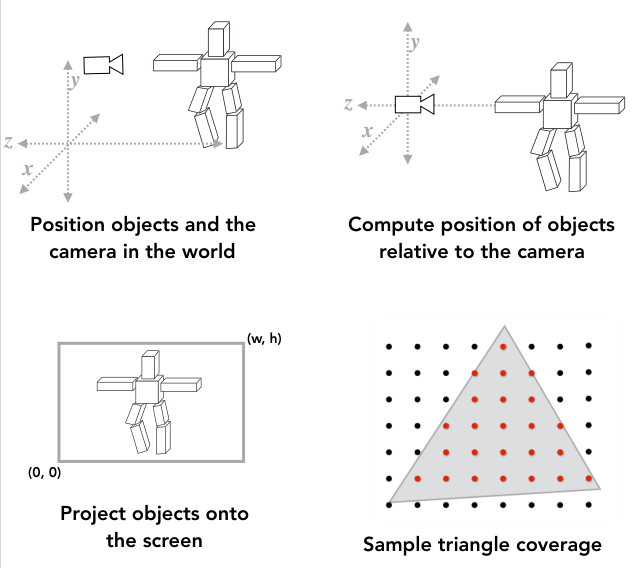
如下图示（顺序：从左到右，从上到下）

1. 模型变换（Model Transformation）：即咱们先把机器人摆成我们要的某种pose，摄像机也放在真实世界某个位置。
2. 视图变换 （View Transformation）：把相机始终放在(0,0,0)位置，然后计算物体相对于相机的坐标位置。（其实相机拍的是机器人正面，为了方便理解才没有把机器人侧着画）
3. 3D位置信息确定好了之后，我们就需要做投影变换，即把3D映射到2D。
4. 得到2D位置信息后，我们需要做光栅化，即确定具体的像素位置。

上面介绍了如何解决可见性（遮挡）问题，比如用Z-Buffer确定了每个像素点的深度和颜色信息，但是是不是单纯把颜色复制到每个像素上就完事了呢？我们先看一下下面两个图片：可以看到右图明显要真实一些，而左图就emm。。。所以为了让图片更真实，下一步我们还需要给物体着色

2.2 定义

在真正开始介绍着色方法之前，先看看shading的定义：

• Merriam-Webster Dictionary

Shading：The darkening or coloring of an illustration or
diagram with parallel lines or a block of color.

• 本节课的定义:

The process of applying a material (材质) to an object.

注意shading(着色)≠shadow（阴影） 。

2.3 Blinn-Phong Reflectance Model

Blinn-Phong Reflectance Model (BPRM) 是一个比较简单的着色模型。 Blinn和Phong是两个人的名字。

下图给出了一个示例：

可以看到光源应该在右上角，图片有如下几个特点：

• Specular highlights：镜面高光。即当光打在一个表面光滑的物体上时，就会产生镜面反射。
• Diffuse reflection：漫反射。像墙这一类表面粗糙的物体，光打在它们身上是会朝四面八方反射。
• Ambient lighting：环境光。我们知道人之所以看得见物体是因为物体把光反射到了我们的眼睛。那为什么我们能看到最下面的那个绿色杯子的背面呢？按理说右上角的光应该照不到那块啊。我们之所以能看到，其实就是因为环境光的原因，简单理解就是，右上角的光源打在墙上，然后通过漫反射又把光打在了桌子和绿色杯子的背面，所以我们就看得见了。简单理解环境光就是二次光。

2.3.1

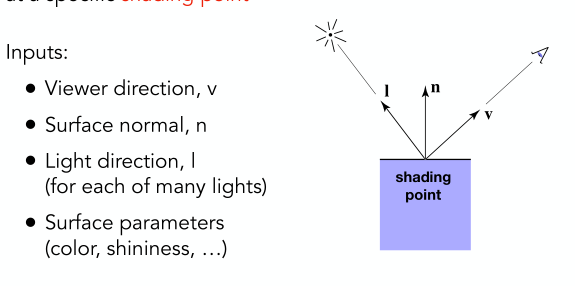
为方便理解，我们现在来看看一个局部点的着色问题（非常小的一个局部可以近似成直线）。可以看到定义了如下几个东西：

• 观测方向（view direction）:着色点到相机的方向，即\(\vec{v}\)
• 表面法向（surface normal）：垂直着色点的反向，即\(\vec{n}\)
• 光的方向（light direction）：着色点到光源的方向，即\(\vec{l}\)。注意起点也是着色点，而不是光源，这是一种约定俗成的规定，也是对编程模型的预约定，这样可以不引入光源数据结构，只从着色点出发做处理，这样会简便很多。
• 表面参数（surface parameters）: color，shininess（比如光的亮度）

(上面定义的向量都为单位向量)

下图给出了着色的一个示例图，可以看到物体的明暗都画出来了，但是因为前面提到的，光的方向被定义成从着色点到光源，所以一些应该有阴影的区域没有被画出来，所以我们需要把着色和阴影区分开来。

2.3.2 漫反射

漫反射理论上是指光达到某一点后朝着四面八方均匀的反射出去，如下图示。

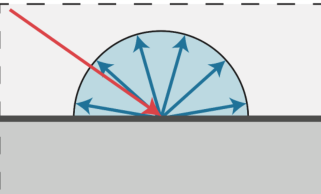
另外我们如何判断物体表面光的亮度呢？看下面的图（Lamber's cosine law）。

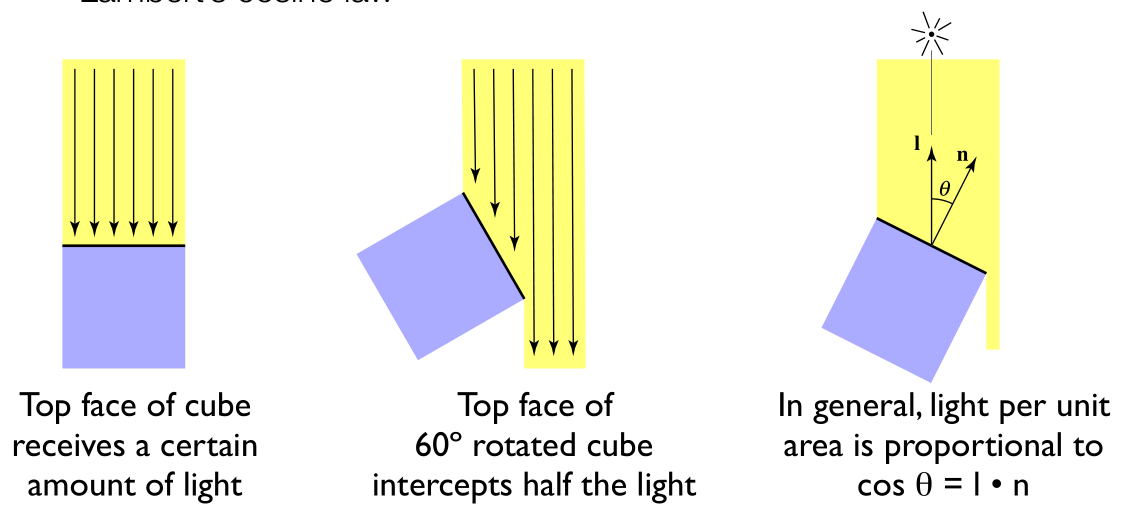
首先为了方便理解，我们假设光是离散分布的，比如左图，对于平放的物体，一共有6条光线打在上面。而我们把物体旋转之后(中间)，此时该表面只接受了三条光线，所以该物体表面肯定要暗一些。仔细观察可以知道，物体表面的亮度应该与一个夹脚有关系，即法线\(\vec{n}\)和光线\(\vec{l}\)夹角。有\(\cos \theta=\vec{l} \cdot \vec{n}\)

我们也可以从另一个角度来理解下图：假设下左图表面是一个边长为1的正方形，那么此时由于光线垂直该表面，所以单位面积接收到的能量是最多的，而旋转一定角度后，很显然单位面积接收到的光线能量就变小了，所以对应地，旋转后的表面的亮度就会暗一些。

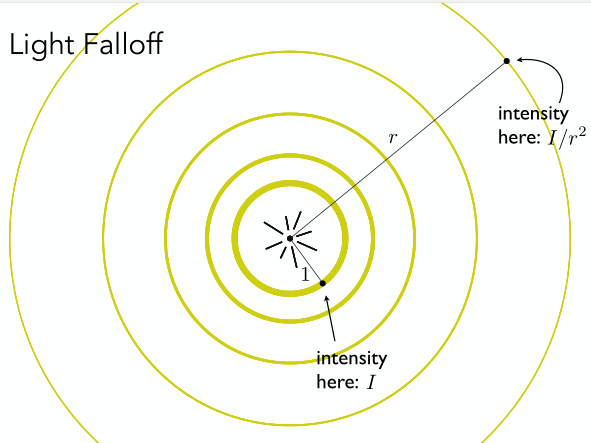
下面介绍了光衰减的原理。中心点是光源，我们假设光在传播过程中能量没有损失，也就是说以该光源为球心的整个球面都是一样的。什么意思呢？

我们假设半径为\(r\)的球面的能量是\(E\)。由于我们假设光在传播过程总能量没有损失，所以\(r\)无论取什么值，其所对应的球面的能量都为\(E\)，这个应该很好理解。

我们再具体分析某一个点，我们假设半径为1的球面上的某一个点的能量是\(I\),那么就由\(E=4\pi \times 1^2 \times I=4\pi I\)。同理，对于半径为\(r\)的球面上的某一个点，该点的能量应为\(E/(4\pi r^2)=I/r^2\)。由此我们可以知道，所有球面的能量虽然是相等的，但是每个点的能量确实不同的，具体来说是衰减的，这也叫做light falloff

结合前面提到的Lamber's cosine law和light falloff，我们可以知道每个着色点的光亮程度计算公式如下：

\[L_{d}=k_{d}\left(I / r^{2}\right) \max (0, n \cdot l) \]

• \(k_d\)指漫反射系数（diffuse coefficient），也叫Diffusivity，代表了颜色信息。什么意思呢？我们知道物体之所以有颜色，是因为它吸收了部分光，反射了剩余的光。比如黑色就是把所有光的吸收了，没有光被反射，因此是黑色。又比光照在橘子上，橘子吸收了除橙色以外的光，因此最后橙色的光反射到人眼，所以橘子看起来就是橙色的了。很显然，吸收的光越多，那么能量就越大，不同能量也就对应了不同颜色的光，所以说这个系数也可以指代颜色。具体来说，如果\(k_d\)是一个标量，那就应该表示明暗（黑白）程度，如果是一个三通道的向量，那么就可以表示具体的颜色了。 从微观角度看，再平直的表面都存在凹凸不平，因此就存在光向四周漫射的现象。向四周漫射的光通量与总的反射光通量之比称为：漫射系数或漫反射系数。这个与物体材质有关。
• \(\max (0,n \cdot l)\)：为什么这里要取最大值呢？因为前面提到了，单位面积接受到光的能量与 法向和光线夹角有关，而我们一般认为，如果夹角的绝对值大于90°时没有意义，就好像下图的光线是从下方打过来的，此时该着色点被其他的点遮住了，故认为该点能量强度为0.

再仔细分析上面的公式可以知道，物体表面的颜色或者明暗程度与观测点（相机）的位置无关，即与\(\vec{v}\)无关，这与现实世界也是相符合的。比如你看月亮，它的表面亮度不会随着你的移动而发生改变，相反它只与太阳光的方向以及法线方向有关。

下图给出了光源处在不同位置时观测到的球面明暗程度的变化。以最右边那个为例，可以知道光源应该是左上方，照射到球面后，左上角球面的法向和光线方向夹角很小，所以看起来明亮一些；而随着夹角\(\theta\)达到90°，甚至超过90°后，基本上就变成黑色了，这个通过上面的公式也可以很清楚的看到。

微信公众号：AutoML机器学习
MARSGGBO♥原创
如有意合作或学术讨论欢迎私戳联系~
邮箱:marsggbo@foxmail.com
2020-04-27 21:36:02