【GAMES101-现代计算机图形学课程笔记】Lecture 05 Rasterization 2 (Antialiasing and Z-Buffering)
1. 回顾和本节摘要
1.1 上一节内容回顾
- Viewing
- View + Projection + Viewport(将cuboid变换到屏幕空间)
- Rasterizing triangles
- Point-in-triangle test
- Aliasing:像素引起的锯齿状失真。
1.2 本节内容概要:
- Antialiasing
- Sampling theory
- Antialiasing in practice
- Visibility / occlusion
- Z-buffering
下图给出了Alias(图像失真)的例子。最左边是计算出的在三角形内的像素中心点,中间是我们想要得到的效果,右边是实际效果。买家秀和卖家秀。。。这个现象的学名就叫aliasing。下面主要介绍如何防止失真走样。

2. Sampling Artifacts (SA)
在图形学里,artifacts指的是Errors / Mistakes / Inaccuracies,泛指一些不准确或者与我们预期不一样的结果。
SA有如下几类:
- Jaggies – sampling in space
- Moire – undersampling images
- Wagon wheel effect – sampling in time
- [Many more] …
主要原因是因为信号变化太快,而采样太慢。
一种反走样(Antialiasing)的方法是对原图先做模糊处理(滤波),然后再采样。效果可以看下面几个示例


但是如果我们先采样,然后再滤波,效果如下图左边,可以看到效果并不好。为什么采样和滤波的顺序这么重要呢?下面从频域角度对这一现象进行介绍和分析。
3. Frequency Domain (频域)
3.1 傅里叶级数
傅里叶级数能将任何周期函数或周期信号分解成一个(可能由无穷个元素组成的)简单振荡函数的集合,即正弦函数和余弦函数(或者,等价地使用复指数)。
傅里叶级数展开示例:

3.2 走样
前面提到走样的原因是信号变化太快,而采样太慢。观看这句话可能不太能理解,但是结合下面的图应该就很好理解了。
可以看到有五条不同的绿色曲线,分别表示不同的信号。黑色的点表示每隔一段时间对信号采样得到的点。可以看到对于\(f_1(x)\),因为他的频率较慢,所以我们通过连接采样得到的黑点其实大致上还是能还原出原信号的。而随着信号频率不断增加,以\(f_5(x)\)为例,此时很显然我们无法还原信号了。

3.3 Filtering(滤波)
滤波表示去除某种特定的频率(如高频、低频)信息。
下图是原图:

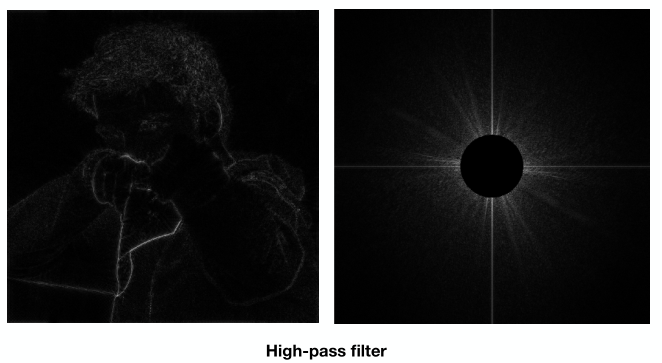
- high-pass filter 高通滤波
下图展示了高通滤波的效果。高通即只有高频信息留下,而滤掉低频信息。那什么是高、低频信息呢?
简单理解就是颜色变化剧烈的就是高频信息,比如上面右图中心基本上都是白色的,这就是低频信息,所以使用高通滤波后中间的光亮就被去掉了。同理,对于左图而言,高频信息指的就是那些边界,因为边界的颜色或者光亮变化更强烈,可以看到最后剩下的是人的轮廓。
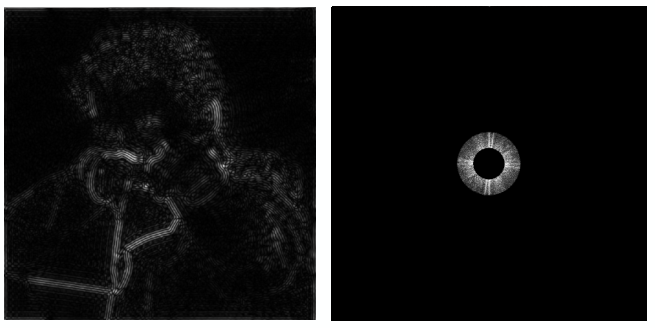
- low-pass filter 低通滤波

- band-pass filter 带通滤波
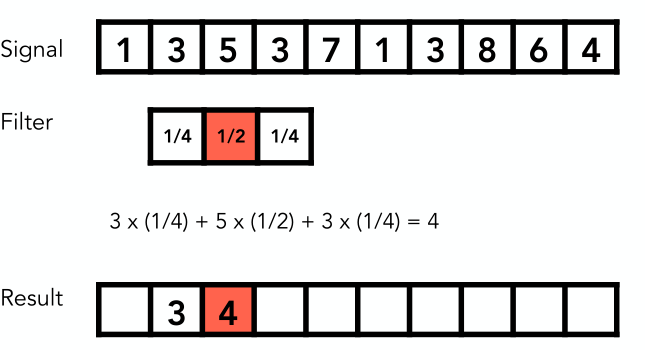
3.4 卷积(convolution)
通过上面的分析可以知道一张图可以看作是由低频、高频、和其他频段的信号组成的。如果我们想要得到高频信号,那么就等价于给高频信号权重为1,其他频段信号权重为0。换言之,滤波其实就是加权求和,也就是卷积,即
Filtering = Convolution = Average
卷积定理
时域(spatial domain)上的卷积等价于频域(frequency domain)上的乘积;
时域上的乘积等价于频域上的卷积;
比如我对一张图片做卷积操作,等价于我们先把图片和卷积核通过傅里叶变换转化到频域上,然后在频域上将两者相乘(可以理解成乘了一个mask),最后将相乘的结果做逆傅里叶变换即可。
现在我们思考这么一件事情:时域上卷积核的大小和频域上是什么关系? 比如是正相关还是负相关?
答案是负相关。为了方便理解,我们举几个极端的情况。
假设在时域上,卷积核大小是整张图的大小,那么简单理解就是把图片上所有像素的值做平均,这样得到的值肯定和原来像素值差别很大,最后得到的图片应该是非常模糊的,换句话说图片里很多信息都丢掉了。而前面说了,时域上的卷积等价于频域上的乘积,而这个乘积进一步可以简单理解成就是乘了一个mask,因为图片信息丢掉了很多,那不就代表这个mask的非零值很少吗。总结来说就时域上卷积核越大,那么对应地频域上的卷积核就越小。
(下面给出了两种情况的卷积核示意图,可以看到左边的卷积核小一些,对应到频域上大一些。)

3.5 采样(sampling)
采样等价于重复频率信息。
Sampling = Repeating Frequency Contents
下图左侧(a,c,e)表示时域上的操作,右侧(b,d,f)表示频域上的操作。其中(a)表示时域信号,(b)表示信号在频域上的样子(这里画成三角形是为了好理解,什么样子其实无所谓,不影响理解)。
(c)表示冲激采样,即每隔一段时间就采样一次,它在频率上的其实也和冲激信号长得一样(d)。
在时域上的采样(e)其实就是信号和冲激采样相乘\(x_a(t)\times p_\delta(t)\),那么对应到频域就是二者做卷积(f)。
得到的效果可以看到在频域上其实就是对原频域信号不断的重复。

当然上面给出的是一种比较理想的情况,如果采样间隔较长(或者说采样较慢)的话则会导致下面sparse sampling的情况,即频域信号之间在重复时发生了混叠,及导致了aliasing现象。

(注意:上图表示的是频域上的信号表示,横轴表示频率,纵轴表示幅度,即信号强度)
3.6 反走样(Antialiasing)
上面介绍了走样发生的原因,那么如何反走样呢?
一种本质的方法是提高采样速率。但是很多情况下这不现实,我总不能随便改变一个手机或者电视的刷新频率吧?
那么另外一种替代的方法就是我对信号做截断处理,如下图示。可以看到通过截断高频信号(注意横轴表示频率),这样我们就可以避免了走样现象发生,即实现了反走样。

到此为止,也就解释了我们最前面给的例子,即先对三角形做滤波(模糊操作),然后再采样。

那么对三角形模糊处理具体是怎么做的呢?其实就是在频域上使用低通滤波将器乘以这个三角形的频域信号即可,也就是模糊操作(高通滤波的效果是保留轮廓),那对应到时域上我们可以使用一个像素大小的卷积核对单个像素做卷积操作,什么意思呢?
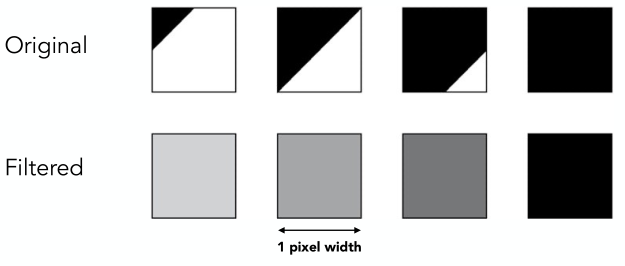
下图给出了单个像素内被三角形覆盖面积的不同情况:
以最左边的像素为例,黑色表示三角形覆盖的面积,可以看到大约是覆盖了1/8的面积,那么做平均之后这个像素对应的亮度值就是纯白色的7/8。
4. Antialiasing By Supersampling (MSAA)
上面对每个像素内部做平均计算不太好计算,所以一种改进的算法MSAA诞生了。
MSAA的大致思路是从逻辑上把一个像素点再细分,比如把一个像素点划分成4个child-points (a→b)。
然后通过child-point覆盖的数量来计算对应的颜色(c,d)
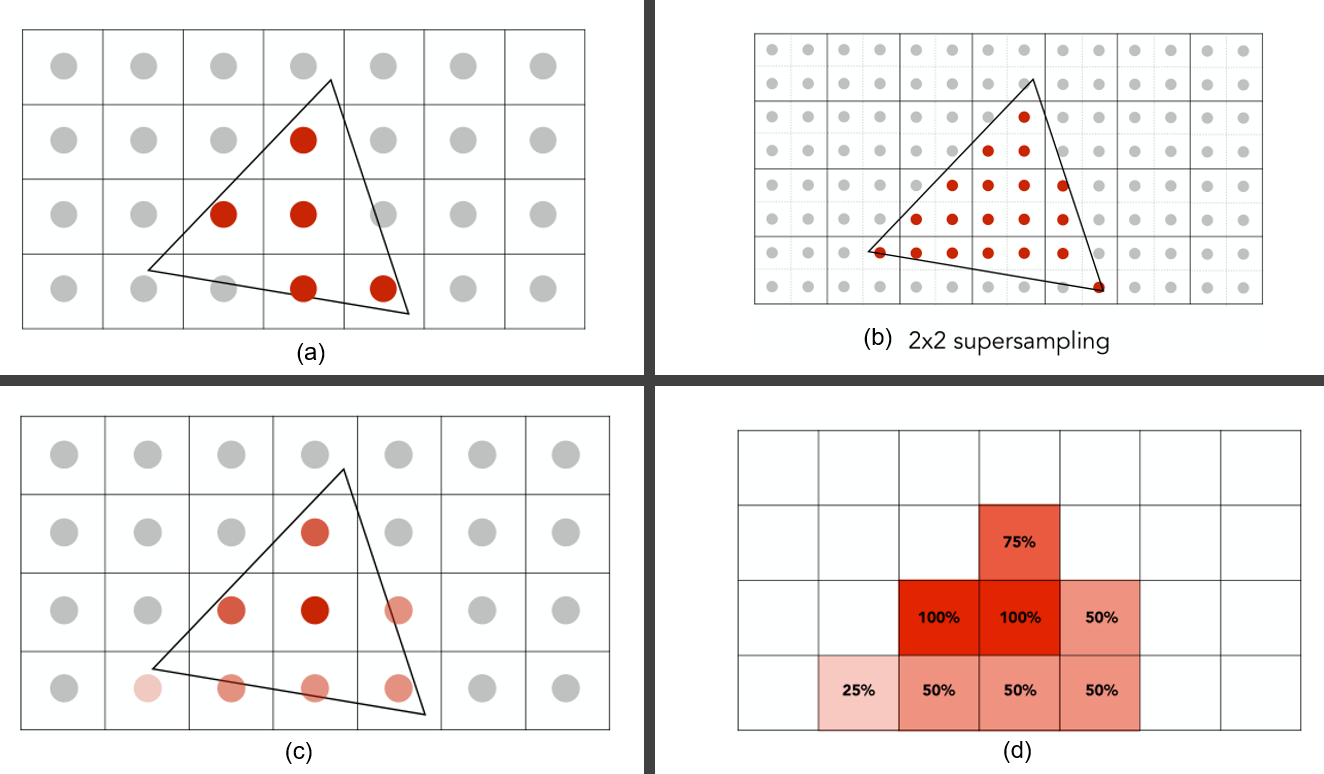
但是MSAA一个很明显的缺点就是计算量增加了4倍。。。
后续又不好改进算法,这里不做详细介绍了:
- FXAA (Fast Approximate AA)
- TAA (Temporal AA)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号