【GAMES101-现代计算机图形学课程笔记】Lecture 04 Transformation Cont.

1. 3D Transformations

这里再上一节内容的基础上对3D 变换做个补充说明

3D下点和向量表示如下：

• 3D point \(=(x, y, z, 1)^{\top}\)

• 3D vector \(=(x, y, z, 0)^{\top}\)

• Scale

\[\mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• Translation

\[\mathbf{T}\left(t_{x}, t_{y}, t_{z}\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• Rotation

• 绕x轴旋转

\[\mathbf{R}_{x}(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• 绕z轴旋转

\[\mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• 绕y轴旋转(需要注意此时sinα的符号和前面两种情况略有不同)

\[\mathbf{R}_{y}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

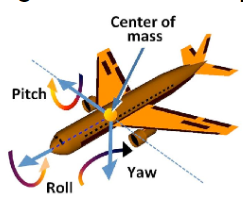
那么总的旋转可表示如下（称作Euler angles）：

\[\mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_{x}(\alpha) \mathbf{R}_{y}(\beta) \mathbf{R}_{z}(\gamma) \]

Euler angles常用在飞机的旋转，即旋转划分成roll,pitch,yaw三个操作。

Rodrigues’ Rotation Formula
\(n,\alpha\)分别表示旋转轴向量和角度

\[\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathrm{N}}\]

2. Viewing (观测) transformation

2.1 View (视图) / Camera transformation

什么是视图变换呢？

下面以拍照为例进行介绍

• Find a good place and arrange people (model transformation)
• Find a good “angle” to put the camera (view transformation)
• Cheese! (projection transformation)

2.1.1 相机的定义

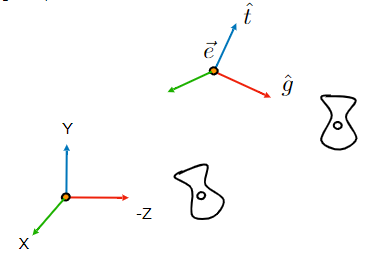
那么相机需要定义如下几个向量：

• position \(\vec{e}\): 即我的相机摆在什么位置
• look-at / gaze direction \(\hat{g}\): 即相机的朝向
• up direction \(\hat{t}\): 表示相机镜头摆放方向，比如我们可以把相机横着拍，也可以正着拍。（自动脑补一下有时候摄像师为了拍摄好看的照片各种骚姿势）

一般来说我们希望相机始终位于原点，而且相机是正摆放的(Y轴正方向)，拍摄方向是朝着正前方拍的(Z轴负方向)。

假设摄像机的初始状态如右上角坐标所示，我们首先需要将其变换到左下角的坐标上去。

2.1.2 矩阵变换

那么矩阵形式如何表示呢？前面内容讲过，我们可以先把相机平移到原点，然后再做线性变化，表示如下：

\[M_{\text {view}}=R_{\text {view}} T_{\text {view}} \]

• 平移到原点

\[T_{v i e w}=\left[\begin{array}{cccc} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{array}\right]\]

• 旋转

将 \(\hat{g}\) 旋转到 \(-Z\), \(\hat{t}\) 旋转到 \(Y\), \(\hat{g}\times \hat{t}\) 旋转到 \(X\)。但是直接求这个旋转变换有点困难，所以一个讨巧的办法是我们求逆变换，即我们先求\(Z\) 旋转到 \(\hat{-g}\)，\(Y\) 旋转到 \(\hat{t}\)，\(X\) 旋转到\(\hat{g}\times \hat{t}\) ，此时逆旋转变换矩阵如下：

\[R_{v i e w}^{-1}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0 \\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0 \\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\]

上一节中有介绍旋转矩阵是正交矩阵，而正交矩阵的性质是\(A^T=A^{-1}\)，那么要求的的旋转变换矩阵，我们只需要对逆变换矩阵做转置即可求得：

\[R_{v i e w}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\]

注意上面的\(x_{\hat{g} \times \hat{t}} , y_{\hat{g} \times \hat{t}} , z_{\hat{g} \times \hat{t}},x_t\)等是view坐标系下的坐标值，而不是在世界坐标系(\(XYZ\))。

总结： 介绍了这么多，我们为什么要大费周折的做这些变化呢？模型中的有很多顶点，这些顶点坐标是模型空间下的，而我们通常做变化都是以世界坐标为基准的，所以我们需要做模型变换。

2.2 Projection (投影) transformation

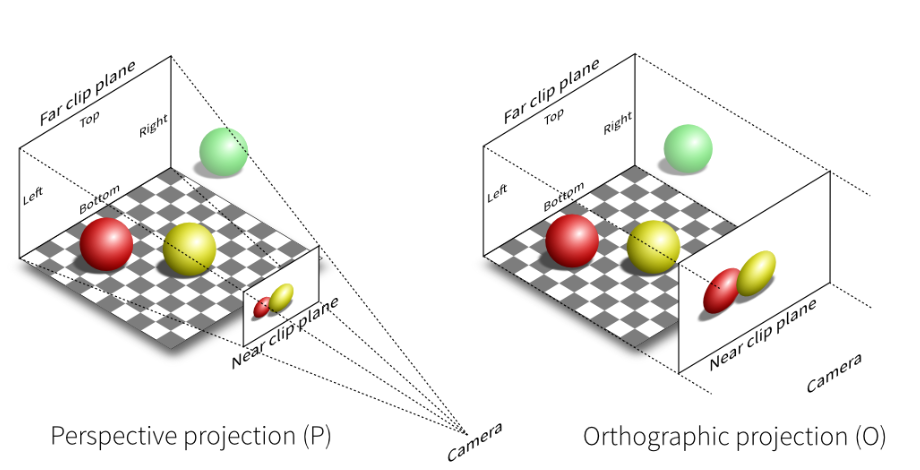
投影变化有两种实现方法，分别是正交投影和透视投影，示意图如下：

2.2.1 Orthographic (正交) projection

• 一个简单的理解方式

对于正交投影而言，结合下图来理解，相机位置放在原点，朝着\(-Z\)方向拍摄，相机正向摆放，即沿着\(Y\)方向，那么投影之后得到的东西在X-Y平面上，换句话说就是把Z轴丢掉了。不过有一点需要注意的是，投影之后一般还会把投影图像缩放成一个边长为2的正方形，即\([-1,1]^2\),这种做法是约定俗成的，另外也是方便后面的操作。

你可能会想问，这样做不是会把物体做了拉伸了吗？没错是拉伸了，所以一般在后面的操作中还会再做一次拉伸来还原的。

• General 操作步骤

我们有一个长方体(cuboid),表示为 \([l,r] \times [b,t] \times [f,n]\)，其中\(l,r\)表示在X轴上的左(left)右(right)顶点坐标值，同理\(b,t\)表示Y轴上的下(bottom)上(top)坐标,而\(f,n\)表示Z轴上远(far)近(near),这个需要注意的是因为我们默认相近朝着Z轴负方向，所以Z轴坐标值越大，表示越近，反之越远。

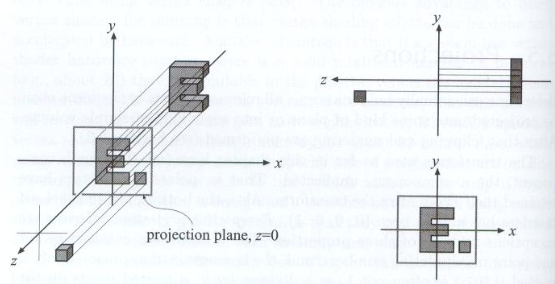
确定了长方体的表示后，我们需要做如下处理（同上面一样），即将长方体映射为canonical cube(正则、规范、标准正方体)，表示为\([-1,1]^3\)。

具体实现方法则是将长方体中心先平移到原点，然后再做缩放变换即可，用矩阵表示如下（下式中的\(r,l\)等表示坐标值，不是向量。）：

\[M_{\text {ortho}}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]\]

OpenGL 采用的是左手系，所以上面式子中的负号可能相反但不影响理解。

2.2.2 Perspective (透视) projection

在介绍透视投影之前，需要介绍如下齐次坐标的一个性质：

对于3D齐次坐标内的一个点\((x,y,z,1)\)，我们任意乘以一个非零常数\(k\),得到的点\((kx,ky,kz,k)\)仍然表示同一个点。比如\([1,0,0,1]\)和\([2,0,0,2]\)表示的是同一个点\((1,0,0)\)。

下图给出了透视投影(frustum,平截头体)和正交投影的投影例子(Cuboid)。

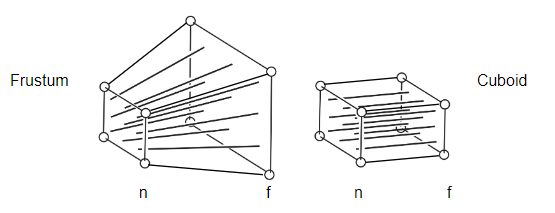
可以看到透视投影其实就是将右边平面(即(\(f\))远平面)的东西投影到左边平面（即近(\(n\))平面），所有投影的线最后都相交于一个点，即视点。而正交投影的投影线互相之间是平行的。

很多教材在介绍透视投影时都是硬生生地给出远平面投射到近平面的公式，这样非常不利于理解。为了方便理解，我们可以把这个投影拆成两步：

1. 我们先将远平面以及中间的那些平面做挤压（squish）（可以想象成把平面的四个顶点往平面的中心点靠拢，使得边长和近平面长度相等）；注意挤压是对所有平面所做的操作。

2. 之后我们再对挤压后的平面再做正交投影即可。

上面第一步骤中的挤压需要满足如下几个条件

• 近平面上任何一个点永远不变。
• 远平面挤压前后的Z值都保持为\(f\)不变
• 远平面的中心点X,Y,Z坐标保持不变

注意远近平面之间的点在做变换之后的Z轴坐标可能是会变的！！！只有远近平面上的点的Z坐标才保持不变（原因在下一讲介绍），这个特别重要，后面计算会用到。

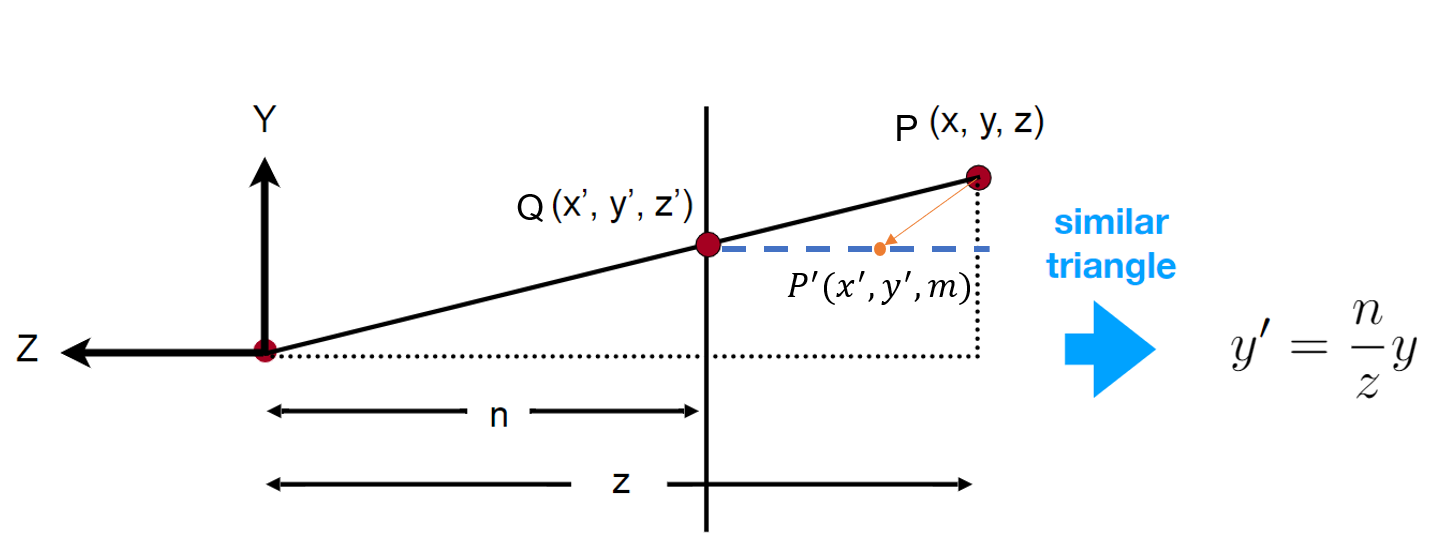
下面我们从侧面来观察远近平面投影特点（看视频的时候我一直以为Q点是P点挤压后得到的点，其实P'才是，Q是P'在近平面上的投影点）：

original point坐标为\(P=(x,y,z)\),transformed point（即挤压之后的点）坐标为\(P'=(x',y', m)\),而\(Q\)是\(P'\)在近平面上的投影点，即二者的X、Y坐标值相等，Z轴坐标不相等。近平面Z轴坐标为\(n\)，远平面为\(f\)。

注意下图中的\(P\)表示远近平面上以及之间的任意点，挤压后的\(P'\)的Z轴坐标可能与原坐标并不相等，即\(m\)不一定等于\(z\)！！！

但是我们根据相似三角形可以得到挤压后的点Y轴坐标等于\(Q\)点的Y轴坐标，即\(y^{\prime}=\frac{n}{z} y\)，同理在X轴上的坐标为\(x^{\prime}=\frac{n}{z} x\),而坐标\(m\)暂不可知。

根据上面的分析可以得到在齐次坐标系下原坐标的变换过程如下(下面最右边的等价是由点的定义得到的，即点坐标乘以一个常数后仍然表示原来的点。)：

\[\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right) \Rightarrow\left(\begin{array}{c} n x / z \\ n y / z \\ m \\ 1 \end{array}\right) \begin{array}{c} \text { mult. } \\ \text { by z } \\ == \end{array}\left(\begin{array}{c} n x \\ n y \\ zm \\ z \end{array}\right) \]

对点坐标的挤压其实等价于左乘一个变换矩阵，等式如下

\[M_{p e r s p \rightarrow o r t h o}^{(4 \times 4)}\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ zm \\ z \end{array}\right) \]

至此可以求得左边矩阵的值为

\[M_{p e r s p \rightarrow o r t h o}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ A & B & C & D \\ 0 & 0 & 1 & 0 \end{array}\right)\]

由于挤压后的点的Z坐标\(m\)并不知道，所以上面矩阵的第三行的值都不能确定，所以用变量\(A,B,C,D\)表示。而要求解第三行的值则需要用到最开始提到的几个需要满足的条件：

1. 近平面上的点保持不变，即挤压前后Z坐标值\(z=m=n\),即有

\[M_{p e r s p \rightarrow o r t h o}^{(4 \times 4)}\left(\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ zm \\ z \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ n^2 \\ n \end{array}\right)\]

进一步求解可得：

\[\begin{aligned} &A x+B y+C z+D=m z\\ &\stackrel{m=z=n}{\longrightarrow} A x+B y+C n+D=n^{2} \\ &\Rightarrow\left\{\begin{array}{l} A=B=0 \\ C n+D=n^{2} \end{array}\right. \end{aligned}\]

此时仍然求解不出来，所以我们还需要用到前面的条件

2. 远平面的点的Z坐标保持不变，即\(z=m=f\),同理可求得等式：

\[\begin{aligned} \left\{\begin{array}{l} A=B=0 \\ C f+D=f^{2} \end{array}\right. \end{aligned} \]

现在只需要求解方程组即可，

\[\left\{\begin{array}{l} C n+D=n^{2} \\ C f+D=f^{2} \end{array} \rightarrow\left\{\begin{array}{l} C=n+f \\ D=-n f \end{array}\right.\right.\]

至此我们就完成了第一步骤求解出了挤压矩阵，

\[M_{p e r s p \rightarrow o r t h o}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right)\]

通过上面的挤压矩阵，我们把原来的frustum挤压成了一长方体，那么很自然地第二步骤其实就是使用正交投影即可，而正交投影矩阵前面已经介绍了，所以最终的透视投影矩阵求解公式如下：

\[M_{p e r s p}=M_{o r t h o} M_{p e r s p \rightarrow o r t h o} \]

微信公众号：AutoML机器学习
MARSGGBO♥原创
如有意合作或学术讨论欢迎私戳联系~
邮箱:marsggbo@foxmail.com 2020-04-25 11:01:24