【GAMES101-现代计算机图形学课程笔记】Lecture 03 Transformation

1. Why study transformation

1.1 Modeling

• translation (平移)
• rotation（旋转）
• scaling （缩放）
• projection （投影）

2. 2D transformations: rotation, scale, shear

我们在求解变换矩阵的时候其实只需要去满足一些特殊点即可算出变换矩阵了，而不需要死记硬背一些公式。具体可以看看旋转矩阵的推导示例。

2.1 Scale (缩放变换)

假设原坐标为\(\left[\begin{array}{l}x \\ y\end{array}\right]\)

• Scale Matrix (缩放矩阵)

通过左乘一个Scale Matrix可以事先缩放变换，例如下式表示x,y坐标都缩放s倍。

\[\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}s & 0 \\ 0 & s\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] \]

• Reflection Matrix (反射矩阵)

Horizontal reflection

\[\left[\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right]=\left[\begin{array}{ll}-1 & 0 \\ 0 & s\end{array}\right]\left[\begin{array}{l}x \\ y\end{array}\right] \]

• Shear Matrix (剪切矩阵)

剪切变换(shear transformation)是空间线性变换之一，是仿射变换的一种原始变换。它指的是类似于四边形不稳定性那种性质，方形变平行四边形，任意一边都可以被拉长的过程。

\[\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} 1 & a \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]\]

• Rotation Matrix (旋转矩阵)

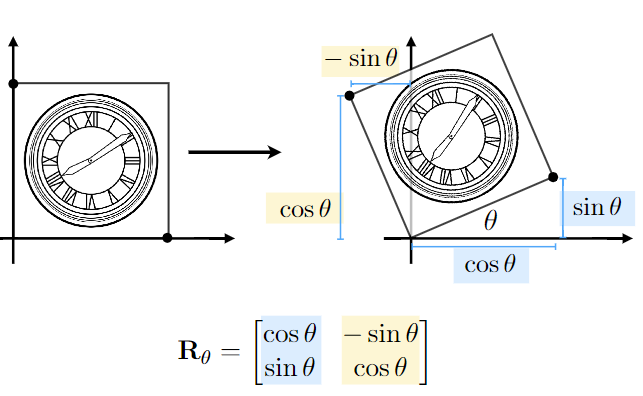
下面以右下角顶点为例进行旋转矩阵计算，计算方法如下(其实就是求解方程组)：

假设原坐标为(x,y),变换后的坐标为(x',y')，则有

\[\left(\begin{array}{c} x^\prime \\ y^\prime \end{array}\right)=\left(\begin{array}{ll} A & B \\ C & D \end{array}\right)\left(\begin{array}{l} 1 \\ 0 \end{array}\right)\]

为方便表示，假设为正方形边长为1，那么可以得到如下等式

\[\left(\begin{array}{c} \cos \theta \\ \sin \theta \end{array}\right)=\left(\begin{array}{ll} A & B \\ C & D \end{array}\right)\left(\begin{array}{l} 1 \\ 0 \end{array}\right)\]

求解可得\(A=\cos \theta, C=\sin \theta\)

同理将左上角坐标变换代入计算即可求出B,D。

另外旋转矩阵具有一些比较有意思的性质，这些性质在下一节会用到

• 旋转θ角度
  \(R_{\theta}=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right)\)
• 旋转-θ角度
  \(R_{-\theta}=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right)\)

很显然有\(R_{-\theta}=R_\theta^T\),而又由定义可知\(R_{-\theta}=R_\theta^{-1}\),因为这两个操作是互逆的嘛。

也就是说\(R_{-\theta}=R_\theta^T=R_\theta^{-1}\)，而在数学上如果一个矩阵的逆等于它的转置，那么就称这个矩阵为正交矩阵(Orthogonal Matrix)，即旋转矩阵是正交矩阵。

3. Homogeneous coordinates (齐次坐标)

3.1 为什么需要引入齐次坐标呢？

首先看一下平移操作

\[\begin{aligned} &x^{\prime}=x+t_{x}\\ &y^{\prime}=y+t_{y} \end{aligned}\]

转化成矩阵形式如下：

\[\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]+\left[\begin{array}{l} t_{x} \\ t_{y} \end{array}\right]\]

显然上述操作并不能用矩阵乘法来表示，因此平移变换不能像前面的变换操作一样可以直接用矩阵乘法表示，所以为了让平移变换也可以以一种优雅的矩阵乘法形式表示，所以需要引入齐次坐标。

3.2 如何使用齐次坐标

以二维坐标为例，我们可以通过额外加入一个坐标来使用齐次坐标。因此：

• 一个2D的点，可以表示为\((x, y, 1)^{\top}\)
• 一个2D向量，可以表示为\((x, y, 0)^{\top}\)

3D情况同理，表示如下：

• 3D point \(=(x, y, z, 1)^{\top}\)
• 3D vector \(=(x, y, z, 0)^{\top}\)

那为什么点和向量最后一项一个是1，而另一个是0呢？仔细想想这样设计是非常smart的操作，因为它满足了如下性质：

• vector + vector = vector (第三维仍然是0，所以表示向量)
• point - point = vector (这符合我们学习向量时所给出的定义，即某点指向另一个点，那不就表示向量了吗，而且相减之后第三维恰巧就是0)
• point + vector = point (这个很好理解，不再赘述)
• point + point = ?point
  最后一个我们用一个例子来说明，假设两个点分别为\(a=(0, 1, 1)^{\top},b=(0, 3, 1)^{\top}\),那么\(c=a+b=(0, 4, 2)^{\top}\)，因为第三维只能是0或者1，所以我们可以对每一维除以2，那么就可以得到\(c=(0, 2, 1)^{\top}\)，这不就是a，b的中点吗！！！是不是感觉很奇妙！

3.3 Affine Transformations (仿射变换)

为了将上述变换统一起来，所以提出了仿射变换，即

Affine map = linear map + translation
(仿射变换 = 线性变换 + 平移变换)

用齐次坐标可以将仿射变换计算公式表示如下：

\[\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{lll} a & b & t_{x} \\ c & d & t_{y} \\ 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right)\]

2D的线性变化在齐次坐标下的表示形式总结如下：

Scale，Rotation，Translation分别表示如下

\[\begin{aligned} &\mathbf{S}\left(s_{x}, s_{y}\right)=\left(\begin{array}{ccc} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{array}\right)\\ &\mathbf{R}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array}\right)\\ &\mathbf{T}\left(t_{x}, t_{y}\right)=\left(\begin{array}{lll} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array}\right) \end{aligned}\]

4. Composing transforms

上述变换可以组合起来实现各种各样的效果，但是需要注意的是各个变换的顺序是非常重要的，因为矩阵乘法不满足交换律。

因为本课程默认向量表示形式为列向量，所以矩阵变换应该是对向量做成矩阵，比如先对向量旋转45°，然后沿X轴平移一个单位，则可以表示如下：

\[T_{(1,0)} \cdot R_{45}\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos 45^{\circ} & -\sin 45^{\circ} & 0 \\ \sin 45^{\circ} & \cos 45^{\circ} & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]\]

注意：\(R_{45} \cdot T_{(1,0)} \neq T_{(1,0)} \cdot R_{45}\)

推广开来，若干个变换可以表示如下：

\[A_{n}\left(\ldots A_{2}\left(A_{1}(\mathrm{x})\right)\right)=\mathrm{A}_{n} \cdots \mathrm{A}_{2} \cdot \mathrm{A}_{1} \cdot\left(\begin{array}{l} x \\ y \\ 1 \end{array}\right)\]

仔细观察可以知道左边一系列的矩阵相乘其实就等价于一个3x3的矩阵，换句话说一个3x3矩阵可以对2D向量做超级多的变换。

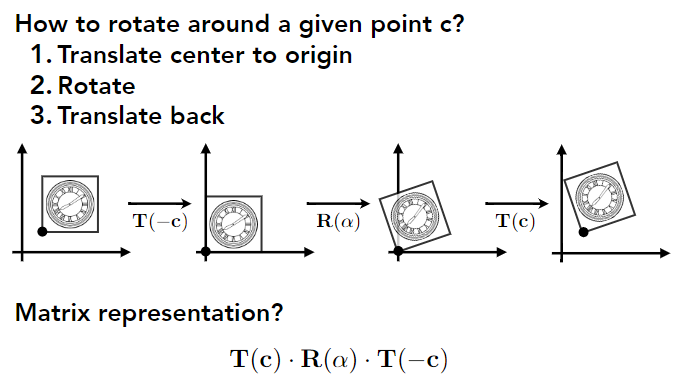
如果一个变化比较复杂该怎么弄呢？很简单我们可以通过对复杂变化做分解来简化，例如如果我们想以下图中（最左边）的正方形左下角为中心进行旋转该怎么做呢？

很简单我们可以先将左下角顶点通过平移变换移动到原点，然后再做旋转，最后将左下角顶点平移回原处即可。

微信公众号：AutoML机器学习
MARSGGBO♥原创
如有意合作或学术讨论欢迎私戳联系~
邮箱:marsggbo@foxmail.com


2020-04-25 09:43:30