【GAMES101-现代计算机图形学课程笔记】Lecture 02 Review of Linear Algebra
1. Vector (向量 / 矢量)
1.1 基础回顾
- 向量表示方式为 \(\vec{a}\) 或者 \(\boldsymbol{a}\)
- 向量长度 \(\|\vec{a}\|\)
- 单位向量表示方式为:\(\hat{a}=\vec{a} /\|\vec{a}\|\)
- 向量表示采用笛卡尔坐标(Cartesian Coordinates),例如
\(\mathbf{A}=\left(\begin{array}{l}x \\ y\end{array}\right) \quad \mathbf{A}^{T}=(x, y) \quad\|\mathbf{A}\|=\sqrt{x^{2}+y^{2}}\)
注意,一般默认向量为列向量。
1.2 向量相乘
1.2.1 点乘
- 定义:
\(\vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta\)
\(\cos \theta=\frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|}\)
- 性质
\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)
\(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\)
\((k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b})\)
- 计算示例
\(\vec{a} \cdot \vec{b}=\left(\begin{array}{l}x_{a} \\ y_{a}\end{array}\right) \cdot\left(\begin{array}{l}x_{b} \\ y_{b}\end{array}\right)=x_{a} x_{b}+y_{a} y_{b}\)
- 用途
1) 计算投影

2) 判断两个向量是否同向
点乘结果>0就表示基本同向,=1表示方向完全一致。
1.2.2 叉乘
- 定义
\(a \times b=-b \times a\)
\(\|a \times b\|=\|a\|\|b\| \sin \phi\)
使用右手法则。
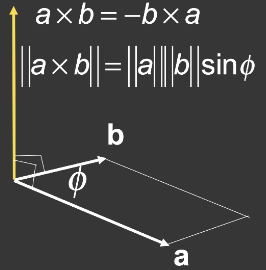
叉乘不满足交换律。
- 用途
1)生成坐标轴
\(\vec{x} \times \vec{y}=+\vec{z}\)
\(\vec{y} \times \vec{x}=-\vec{z}\)
\(\vec{y} \times \vec{z}=+\vec{x}\)
\(\vec{z} \times \vec{y}=-\vec{x}\)
\(\vec{z} \times \vec{x}=+\vec{y}\)
\(\vec{x} \times \vec{z}=-\vec{y}\)
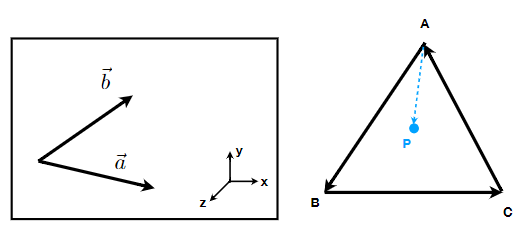
2)判定左 / 右 或者 内 / 外
比如一直坐标系由XYZ组成,然后现在想判断向量b是在a的左边还是右边,之需要求出\(\vec{x} \times \vec{y}\)可以知道与\(\vec{z}\)同向,所以b在a左边。
\(\vec{AP}\)始终在三条有向边\(\vec{AB},\vec{BC},\vec{CA}\)的同一侧(左侧),所以p点在三角形内侧。
注意:三角形三条边的向量必须首尾相连,所以如果我们把下面三角形的三条边向量换一个方向,但是因为最后可以算出AP都在三条边的右侧,即同一侧,所以P点在三角形内侧。
2. Matrix (矩阵)
矩阵在图形学里常用于表示变换(Transformations),比如 translation,rotation,shear,scale等。
矩阵相乘运算
\(\left(\begin{array}{ll}1 & 3 \\ 5 & 2 \\ 0 & 4\end{array}\right)\left(\begin{array}{llll}3 & 6 & 9 & 4 \\ 2 & 7 & 8 & 3\end{array}\right)=\left(\begin{array}{cccc}9 & ? & 33 & 13 \\ 19 & 44 & 61 & 26 \\ 8 & 28 & 32 & ?\end{array}\right)\)
以右边那个8为例,可以看到它是第三行第一列,所以直接找到左边矩阵的第三行,即 \([0\,\,4]\),和右边矩阵第一列 \([3\,\,2]^T\),然后做点积即可求得为8.
-
性质
-
\((\mathrm{AB}) \mathrm{C}=\mathrm{A}(\mathrm{BC})\)
-
\(A(B+C)=A B+A C\)
-
\((\mathrm{A}+\mathrm{B}) \mathrm{C}=\mathrm{AC}+\mathrm{BC}\)
-
矩阵转置:\((A B)^{T}=B^{T} A^{T}\)
-
对角矩阵:只有对角线上有非零元素
-
单位矩阵:对角线上全为1的对角矩阵
-
矩阵的逆:
- \(A A^{-1}=A^{-1} A=I\)
- \((A B)^{-1}=B^{-1} A^{-1}\)
矩阵乘法转化成矩阵形式
- 点积
- 叉乘
\(\vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc}0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0\end{array}\right)\left(\begin{array}{l}x_{b} \\ y_{b} \\ z_{b}\end{array}\right)\)
注意 : A*b的*不表示乘法


