概率密度估计介绍
在学概率论时,常常会看到各种稀奇古怪的名字,有的书上只介绍了该如何求解,但是从不介绍为什么这么叫以及有什么用,本文就介绍一下概率密度估计是什么以及是干什么用的,主要参考Jason BrownLee大神的一篇博文进行介绍。
后面部分名词会以英文缩写形式介绍,汇总如下:
- 概率密度 (probability density, PD)
- 概率密度函数 (probability density function, PDF)
- 概率密度估计 (probability density estimation, PDE)
PD&PDF&PDE之间的关系
一句话概括概率密度就是: 概率密度是观测值与其概率之间的关系
一个随机变量的某个结果可能会以很低的概率出现,而其他的结果可能概率会比较高。
概率密度的总体形状被称为概率分布 (probability distribution),常见的概率分布有均匀分布、正态分布、指数分布等名称。对随机变量特定结果的概率计算是通过概率密度函数来完成的,简称为PDF (Probability Dense Function)。
那么概率密度函数有什么用呢?很有用!例如我们可以通过PDF来判断一个样本的可信度高低,进而判断这个样本是否是异常值。另外有时我们的输入数据如果要服从某个分布也需要用到PDF。
但是通常我们是不知道一个随机变量的PDF的,因此我们需要不断去逼近这个PDF,而逼近的这个过程就是概率密度估计。
在对随机变量进行密度估计的过程中,需要执行几个步骤。
第一步是用一个简单的直方图来检查随机样本中观测值的密度。从直方图中,我们可以识别出一个常见的、易于理解的可用概率分布,例如正态分布。如果分布很复杂,我们可能需要拟合一个模型来估计分布。
在接下来的小节中,我们将依次仔细介绍这些步骤。
为了简单起见,我们将重点介绍单变量数据,例如一个随机变量。虽然这些步骤适用于多元数据,但随着变量数量的增加,它们会变得更具挑战性。
密度直方图
直方图是这样一种图,它首先将观察结果分组到各个箱子(bin)中,然后计算每个箱子中的事件数量。每个箱子里的计数或观察频率然后用条形图表示,箱子在x轴上,频率在y轴上。
箱子数量和大小的设置也是有讲究的。比如说观察值的范围是1到100,那么我们可以有如下两种方式的划分:
- 3个箱子 (1-33,34-66,67-100):划分比较粗粒度
- 10个箱子 (1-10,11-20,...,91-100):划分更加细腻度,能更好提取密度信息,但是计算量会更大一些
用python来实现一下正态分布的效果
# example of plotting a histogram of a random sample
from matplotlib import pyplot
from numpy.random import normal
# generate a sample
sample = normal(size=1000)
# plot a histogram of the sample
pyplot.hist(sample, bins=10)
pyplot.show()
pyplot.hist(sample, bins=3)
pyplot.show()
结果如下:(左边为bin=10,右边为bin=3)
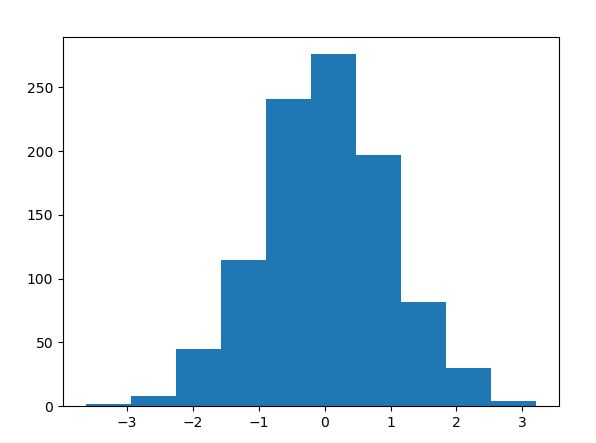
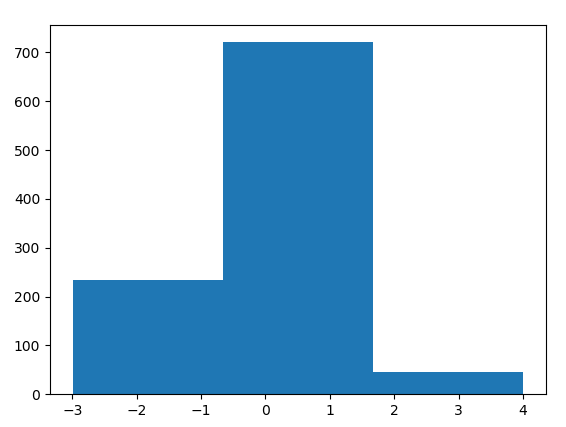
参数密度估计
大多数随机样本的直方图形状都会与一些大家都熟知的概率分布相匹配。因为这些概率分布经常会在在不同的或者是意料之外的场景反复出现。熟悉这些常见的概率分布将帮助我们从直方图中识别对应的分布。一旦我们确认直方图服从某个已知分布,那么我们接下来要做的事情就是去估计这个分布的参数,所以叫做参数密度估计
例如上面的例子中,我们看左边的直方图可以大致猜测其服从正态分布,因此后面只需要求出这个正态分布即可。另外我们知道正态分布只由两个参数决定(假设是单变量情况),即均值和方差,因此我们通过求出观测值的均值和方差,我们便求解出了这个直方图所对应的概率密度函数的估计。
实现代码和效果图如下所示:
# example of parametric probability density estimation
from matplotlib import pyplot
from numpy.random import normal
from numpy import mean
from numpy import std
from scipy.stats import norm
# generate a sample
sample = normal(loc=50, scale=5, size=1000)
# calculate parameters
sample_mean = mean(sample)
sample_std = std(sample)
print('Mean=%.3f, Standard Deviation=%.3f' % (sample_mean, sample_std))
# define the distribution
dist = norm(sample_mean, sample_std)
# sample probabilities for a range of outcomes
values = [value for value in range(30, 70)]
probabilities = [dist.pdf(value) for value in values]
# plot the histogram and pdf
pyplot.hist(sample, bins=10, density=True)
pyplot.plot(values, probabilities)
pyplot.show()
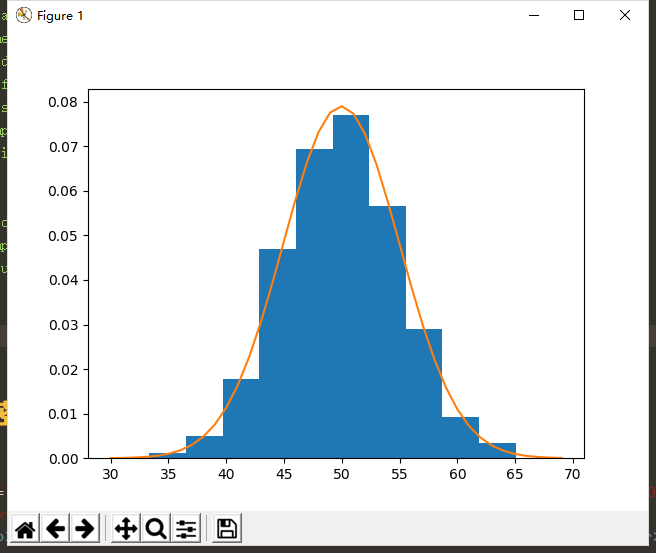
需要注意的是,有的时候我们所观测到的数据并不显示地服从某个已知分布,因此通常我们需要先对数据做一定的变换,之后再来做参数密度估计。
- 比如我们需要先对数据做归一化
- 又或者我们需要先去除一些异常点,因为这些点的存在可能会严重影响后面的密度估计
- 当我们的数据明显左偏(或者右偏)的时候,我们可以对数据取对数或平方根,或者更一般地,使用power转换(如Box-Cox转换)。
参数密度估计的步骤总结如下:
Loop Until Fit of Distribution to Data is Good Enough:
- Estimating distribution parameters
- Reviewing the resulting PDF against the data
- Transforming the data to better fit the distribution
非参数密度估计
在某些情况下,一个数据样本可能不像一个常见的概率分布,或者不容易用某种分布来进行拟合。尤其是当数据有两个峰(双峰分布)或多个峰(多峰分布)时,常常会出现这种情况。这种情况下参数密度估计变得不好使,所以非参数密度估计登场了。
其实非参数密度估计还是有参数的,只不过这个参数和参数密度估计中的参数有所不同。后者的参数是可以直接控制分布情况的,而且参数数量通常是预设好的,例如正态分布的参数就两个:均值和方差。而非参数密度估计其实是使用所有样本来进行密度估计,换句话说每个样本的观测值都被视为参数。常用的估计连续随机变量概率密度函数的非参数方法有核平滑 (kernel smoothing),或核密度估计,简称KDE (Kernel Density Estimation)。
KDE其实就是一个数学函数,它返回随机变量给定值的概率。Kernel(核函数)能够有效地平滑或插值随机变量结果范围内的概率,使得概率和等于1。Kernel根据数据样本的观测值与请求概率的给定查询样本之间的关系或距离,对数据样本中观测值的贡献进行加权。
非参数密度估计有两个重要参数,分别是
-
平滑参数 (smoothing parameter):这个参数有时也叫带宽 (bandwidth)。因为我们每次都是基于多个样本来估计一个新的样本的概率,因此带宽其实指的就是我们根据多少样本来预测新样本的概率,也可以简单理解成滑窗大小。 带宽太大,可能因为损失太多细节而导致粗腻度估计;带宽太小又可能会因为有太多细节使得不够平滑,因此不能足够泛化到其他新的样本。
-
核函数(kernel):用来控制数据集中样本对估计新样本点概率的贡献的函数。
下面也给出一个例子来从直观上来理解非参数密度估计。
下面是当我们设置不同bins值时的两个直方图。可以看到左边有两个峰,右边只有一个。
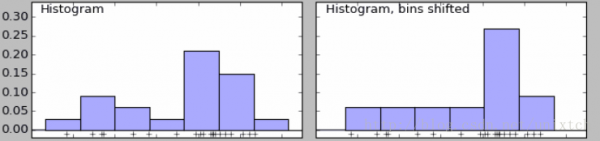
我们也知道当bins增到到样本的最大值时,就能对样本的每一点都会有一个属于自己的概率,但同时会带来其他问题,样本中没出现的值的概率为0,概率密度函数不连续,这同样存在很大的问题。
核密度函数的原理比较简单,在我们知道某一事物的概率分布的情况下,如果某一个数在观察中出现了,我们可以认为这个数的概率密度很大,和这个数比较近的数的概率密度也会比较大,而那些离这个数远的数的概率密度会比较小。
基于这种想法,针对观察中的第一个数,我们可以用K去拟合我们想象中的那个远小近大概率密度。对每一个观察数拟合出的多个概率密度分布函数,取平均。如果某些数是比较重要的,则可以取加权平均。需要说明的一点是,核密度的估计并不是找到真正的分布函数。
Note: 核密度估计其实就是通过核函数(如高斯)将每个数据点的数据+带宽当作核函数的参数,得到N个核函数,再线性叠加就形成了核密度的估计函数,归一化后就是核密度概率密度函数了。
参考:

