矩阵变换小知识

如何将一个任意正方形变换为任意形状的四边形（不知道是否包含凹的啊，这个先不考虑）

仿射变换肯定不行的了，它保持了平行性，即原两条线平行，变换之后还平行
投影变换就可以，因为它仅仅保持了共线性，即只保证一条直线上的点变换之后仍然在一条直线上(参见Multiple View Geometry in computer vision P33)
下面用程序说明一下，具体参见：http://alumni.media.mit.edu/~cwren/interpolator/
先把目标点和对应的点给出来

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
oriD=[(0,0),(0,1),(1,1),(1,0)]
dstD=[(2,1),(3,3),(4,2),(3,0)]
ori=np.array(oriD)
dst=np.array(dstD)
plt.scatter(ori[:,0],ori[:,1],s=30,c=['r','g','b','c'])
plt.scatter(dst[:,0],dst[:,1],s=120,c=['r','g','b','c'])

大点代表变换后的，颜色对应

def getLeft(a,b):
    t1=(a[0],a[1],1,0,0,0,-1*b[0]*a[0],-1*b[0]*a[1])
    t2=(0,0,0,a[0],a[1],1,-1*b[1]*a[0],-1*b[1]*a[1]) 
    dotLeft=t1+t2
    return dotLeft
def getWright(b):    
    return (b[0],b[1])
def getMatrix(x,y):
    A=np.array([getLeft(a,b) for (a,b) in zip(x,y)]).reshape((8,-1))
    B=np.vstack([getWright(b) for b in y]).flatten()
    m=np.linalg.solve(A,B)
    m=np.array(list(m)+[1]).reshape((3,3))
    return m
变换过去：
m=getMatrix(ori,dst)
[m.dot(np.array(list(x)+[1])) for x in oriD]
[array([ 2.,  1.,  1.]),
 array([ 3.,  3.,  1.]),
 array([ 4.,  2.,  1.]),
 array([ 3.,  0.,  1.])]
逆变换也能够变回来：
m_inv=np.linalg.pinv(m)
[m_inv.dot(np.array(list(x)+[1])) for x in dstD]
[array([  3.33066907e-16,   2.22044605e-16,   1.00000000e+00]),
 array([  5.55111512e-16,   1.00000000e+00,   1.00000000e+00]),
 array([ 1.,  1.,  1.]),
 array([  1.00000000e+00,   2.22044605e-16,   1.00000000e+00])]

注：投影变换应使用齐次坐标来理解，变换矩阵又叫齐次矩阵，对于齐次变换，由于矩阵元素的比才是重要的，因此齐次矩阵其实只有8个自由度，计算的时候，将齐次矩阵的[3,3]元素，即角落里那个设为1，源和目标坐标的齐次坐标也设为1

行列式和线性变换

本文源自：http://mathinsight.org/determinant_linear_transformation
T:Rn→Rm 是一个从n维到m维空间的映射，对应一个m*n的矩阵

One-dimensional linear transformations

T(x)=ax
a 看作a 1×1 matrix，行列式就是a

一维变换的行列式对应‘长度’
例如T(x)=3x,将长度拉长为原来的3倍，方向不变

还有 T(x)=−1/2，行列式为负，将朝向改变，实际是就是‘镜像’了

Two-dimensional linear transformations

T:R2→R2
\({T}(x,y) = (ax+by,cx+dy) = \left[\begin{array}{cc}a &b\\ c &d\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right],\)

更简洁一点
\(\{T}(\vc{x}) = A\vc{x},\)
We will view T as mapping objects from the xy-plane onto an x′y′-plane: (x′,y′)=T(x,y).

\(\vc{T}(x,y) = \left[\begin{array}{cc}-2 &0\\ 0 &-2\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right].\)
行列式为4，不改变朝向，即顺时针旋转过来，各个颜色还能对应上

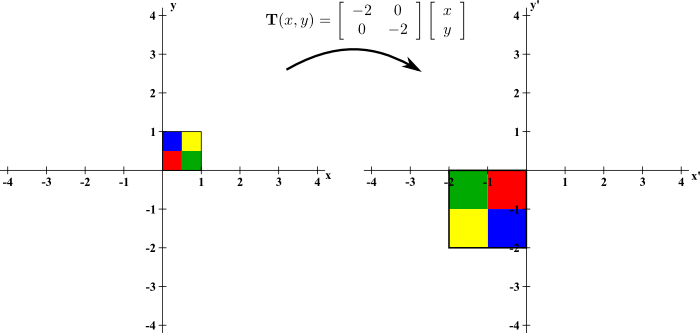
下面这个就不同了，顺时针旋转过来，各个颜色对应不上了

Three-dimensional linear transformations

T:R3→R3改变的是体积和朝向