交叉熵相关

1.交叉熵与最大似然估计之间的联系
结论：交叉熵最小即似然值最大，让模型输出的分布尽量能接近训练数据的分布。
参考链接：
https://www.zhihu.com/question/65288314/answer/849294209

比如说现在有一个真实分布为 P（x）的随机变量，我们对它进行了N次独立同分布实验，对于每个可能的结果x观察到的次数为N（x），利用乘法公式，每次实验的概率乘起来，合并相同的项写成幂的形式。那么它的似然值就可以写成

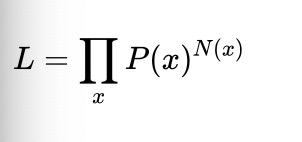
取对数值如下：

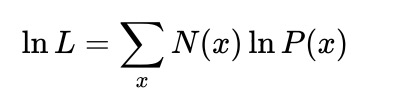
为了避免负数以及避免与样本数之间的直接关系，对上式取负值并除总样本数进行归一化，可得如下：

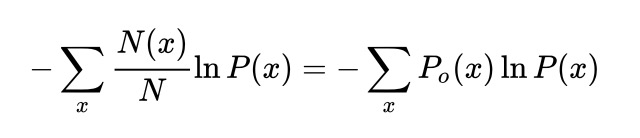
利用拉格朗日乘子法，在给定 Po的情况下，使交叉熵最小的分布P一定有 P=Po，

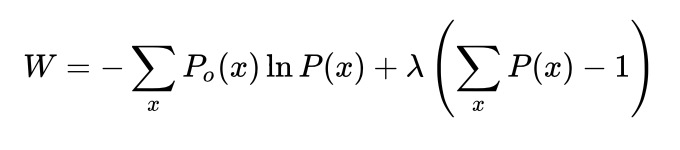
对P（x）求偏导可得

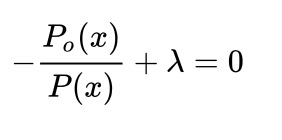
再根据归一化条件得到P=Po。

2.交叉熵损失函数与平方损失函数之间的异同

结论：MSE是高斯分布的最大似然（我们假设： 观察值本身存在的随机性，我们假设这一随机性符合高斯分布。）；CE是多项式分布的最大似然；（标签服从伯努利分布（推广到多分类单标签问题，标签服从多项式分布））分类的问题中，最好检验准确度的模型就是这个预测对还是不对，对为1，不对为0。而MSE是计算你的预测离真实值远不远，因此不适于分类问题。（交叉熵损失函数只和分类正确的预测结果有关。而平方损失函数还和错误的分类有关，平方损失函数除了让正确分类尽量变大，还会让错误分类都变得更加平均。但是对于回归问题这样的考虑就显得重要了，因而回归问题上使用交叉熵并不适合。）同时，MSE作为二元分类的损失函数会有梯度消失。

理论解释如下：

3.LR为什么采用sigmoid函数

1）. 线性模型的输出都是在[−∞,+∞]之间的，而Sigmoid能够把它映射到[0,1]之间。正好这个是概率的范围。
2）. Sigmoid是连续光滑的。
3）. 根据Sigmoid函数，最后推导下来逻辑回归其实就是最大熵模型，根据最大似然估计得到的模型的损失函数就是logloss。这让整个逻辑回归都有理可据。
4）. Sigmoid也让逻辑回归的损失函数成为凸函数，这也是很好的性质。
5）. 逻辑回归的损失函数是二元分类的良好代理函数，这个也是Sigmoid的功劳。