我的俄语物理笔记
这是我的俄语物理笔记。在这里共享给大家。
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
转载请注明出处。
上次更新：2021年05月31日。
更新Log：
2021.05.31：明天考物理了，不会再更了。祝我能顺利通过。
2021.05.04：新增电学。终于到了熟悉的领域。
2021.04.17：新增热力学。真难，同学说这是工热，这是我一个机电本科生应该学的内容吗？
基本 Элементарный
关于物理
-
Что такое физика? Физика – это наука о природе.
-
Что изучает физика? Физика изучает явления природы, свойства веществ и тел, строение молекул и атомов.
单位
注意单位也符合1为原型，234为2格，5以上为复2格。
长度
| 符号 | 俄文 | 数值 | 中文 |
|---|---|---|---|
| м | метр | 1 | 米 |
| см | сантиметр | \(10^{-2}\) | 厘米 |
| мм | миллиметр | \(10^{-3}\) | 毫米 |
| мкм | микрометр | \(10^{-6}\) | 微米 |
| нм | нанометр | \(10^{-9}\) | 纳米 |
| пм | пикометр | \(10^{-12}\) | 皮米 |
| км | километр | \(10^{3}\) | 千米 |
时间
| 符号 | 俄文 | 中文 |
|---|---|---|
| с | секунда | 秒 |
| мин | минута | 分 |
| ч | час | 小时 |
| сут | сутки | 天 |
| неделя | 星期 | |
| месяц | 月 | |
| год | 年 |
速度
| 符号 | 俄文 | 中文 |
|---|---|---|
| м/с | метр в секунду | 米/秒 |
| км/ч | километр в час | 千米/小时 |
体积
| 符号 | 俄文 | 中文 |
|---|---|---|
| л | литр | 升 |
基本物理量
| 俄文 | 中文 | 符号 | СИ单位 (Единицы измерения) |
单位的俄文 | 其他 |
|---|---|---|---|---|---|
| время | 时间 | t | с 秒 | секунда | |
| температура | 温度 | t° | К 开 | кельвин 开尔文 | градусов Цельсия 摄氏度 |
| плотность | 密度 | ρ | кг/м³ | г/см\(^3\) 读作 грамм на сантиметр в кубе. | |
| масса | 质量 | m | кг 千克 | килограмм | |
| энергия | 能量 | E | Дж 焦 | джоуль 焦耳 | |
| длина | 长度 | l | м 米 | метр | |
| площадь | 面积 | S | м² | квадратный метр | |
| скорость | 速度 | \(\vec{V}\) | м/с | метр в секунду | |
| сила | 力 | \(\vec{F}\) | Н 牛 | ньютон 牛顿 | |
| ускорение | 加速度 | \(\vec{a}\) | м/с² |
s=[м] 表示路程的单位为米。
一些术语（有的不属于物理范围。记录了做题时碰到的生词）
| 俄文 | 中文 | 举例 |
|---|---|---|
| как функции... | 用以...为自变量的函数表示 | |
| полный | 总（后面可加机械能，速度等词） | |
| размер | 尺寸 | |
| размерность | 维度 | |
| явление | 现象 | |
| величина | 数值 | |
| частица | 微元 | |
| описание | 描述 | |
| определять | 确定，测定 | |
| кривизна | 曲率 | |
| соответственно | 分别地 | |
| проекция | 投影 | |
| колесо | 车轮 | обод колеса 轮圈 |
| стержень | 杆 | |
| основа | 原则 | |
| многочисленный | 大量的 | |
| сформировать | 形成 | |
| определяться | 由……完全确定 | |
| часовой стрелки | 顺时针 | |
| против часовой стрелки | 逆时针 | |
| превращение | 转化 | |
| достаточный | 足够的 | |
| измерение | 测量 | |
| считаться | 被认为是 | |
| случай | 情况 | |
| сосуд | 容器 | |
| уровень | 水平面 | |
| рассмотрение | 研究 | |
| пружина | 弹簧 | |
| пол | 地面 | |
| потолок | 天花板 | |
| подниматься | 上升 | |
| опускаться, снижаться | 下降 | |
| падать | 下落 | |
| подъем | 上升 | |
| снижение | 下落 | |
| болт | 螺栓 | |
| снаряд | 弹丸 | |
| ствол | 炮管 | |
| пуль | 子弹 | |
| попасть + в + 4 | 打中 | попаду, попадёшь, попадут, попал |
| летать - лететь | 飞 | 前面加вы表示飞出 |
| однородный | 均质的 | |
| сплошной | 实心的 | |
| полый, пустотелый | 空心的 | |
| осторожно | 小心地 | 比如 осторожно положили на горизонтальную поверхность 小心地放在水平面上 |
| окажется +5 | 是 | 原型:оказаться |
| шероховатый | 粗糙的 | |
| гладкий | 光滑的 | |
| катушка | 线圈 | |
| нитка | 线 | |
| собственный | 自身的 | 比如 собственная ось 自身的轴 |
| проекция | 投影 | |
| скольжение | 滑动 | |
| относительная доля | 比例 | |
| первоначальный | 初始的 | |
| приращение | 增量 | |
| ...скомпенсированы | 被抵消 |
解题术语
| 俄文 | 中文 | 举例 |
|---|---|---|
| по закону 或 так | 根据如下规则 | Твердое тело вращается вокруг неподвижной оси z по закону \(\phi =at-\beta t^{3}\), где \(a=6,0\) рад/с, \(\beta = 2,0\) рад/с3. |
| зависит от +2 | 取决于 | угол \(\phi\) его поворота зависит от времени как \(\phi = \beta t^{2}\) |
| утверждать | 断言 | |
| из Н.У. (начальное условие) | 根据初始条件 | |
| с учётом | 考虑到 | |
| свяжем неподвижную систему отсчета с шахтой лифта | 在电梯上建立参考坐标系 | |
| как функции...(+2) | 用以...为自变量的函数表示 | 题干中。被坑过一次。 |
力学 механика
Кинематика 运动学 объясняет, как движется тело.
Динамика 动力学 объясняет причины движения тел.
| 俄文 | 中文 | 定义 |
|---|---|---|
| механика | 力学 | |
| движение | 运动 | изменение положения тела в пространстве. |
| он движется | 他在运动 | |
| он не движется或 он находится в покое | 他静止 | |
| движение и покой относительны | 运动和静止是相对的 | |
| остановка | 停止 | 比如время его вращения до остановки t 他旋转直到停止的时间t。 |
| тело отсчёта | 参照物 | тело, относительно которого мы изучаем движение. |
| относительно чего тело [движется/находится в покое] | 相对于xx，xx运动或禁止 | |
| виды движения | 运动形式（如下） | |
| движение по прямой | 直线运动 | |
| по кривой | 曲线运动 | |
| по окружности | 圆周运动 | |
| по эллипсу | 椭圆运动 | |
| по траектории | 沿轨迹运动 |
运动学 Кинематика
| 俄文 | 中文 | 定义 |
|---|---|---|
| кинематика | 运动学 | |
| материальная точка (МТ) | 质点 | Если размерами и формой тела в условиях данной задачи можно пренебречь, то это тело можно рассматривать как материальную точку (МТ). |
| Твёрдое тело 或 абсолютно твёрдое тело | 刚体 | |
| тело (или точка) отсчёта | 参照物（参照点） | |
| система отсчёта | 参考系 | |
| инерциальная система отсчёта (ИСО) | 惯性参考系 | |
| неподвижный | 静止的 | |
| положение | 位置 | \(\vec{r}(t)\) 表示方法：векторный; координатный и естественный |
| перемещение | 位移 | |
| путь | 路程 | \(s(t)\) ；Путь \(s=s(t)\)- расстояние, пройденное точкой вдоль траектории за время \(t\). 过一段时间 \(\tau\) 通过的路程可表达为：путь s, проходимый точкой за время \(\tau\) |
| уравнение траектории | 轨迹的方程 | |
| скорость | 速度 | \(\vec{v}(t)\) со скоростью v=200м/с 以200米每秒的速度 |
| ускорение | 加速度 | \(\vec{a}(t)\) |
| модуль скорости | 速度的模 | \(v(t)\) |
| средняя скорость | 平均速度 | \(<\vec r>\) |
| мгновенная скорость | 瞬时速度 | |
| направление | 方向 | |
| начальный момент времени | t=0时 | |
| основные виды движения твёрдого тела | 基本的运动形式 | поступательное движение 平动 вращательное движение 转动 |
| поступательное | 平动 | |
| вращательное | 旋动 | |
| вращение | 旋转 | Вращение твердого тела относительно неподвижной оси z. 其中，旋转角为\(\phi\) . 旋转的角速度为\(\omega\) ，旋转的角加速度为\(\beta\) |
| вращается | 旋转 | твёрдое тело вращается вокруг оси z с угловой скоростью \(\omega\) |
| угловое перемещение | 角距离 | |
| угловая скорость | 角速度 | \(\omega\) |
| равномерный | 匀速的 | |
| равнопеременный | 匀变速的 | |
| равноускоренный | 匀加速的 | |
| равнозамедленный | 匀减速的 |
描述物体运动有两种方法，矢量法(векторный)和坐标法(координатный)，其中坐标法相当于把矢量描述拆解成i、j、k向量描述，比如\(\vec{r}(t)=r_{x}(t)\vec{i}+r_{y}(t)\vec{j}+r_{z}(t)\vec{k}\)
对于曲线运动，有 \(\vec{a}=\vec{a_{n}}+\vec{a_{\tau}}\) ,
其中 \(a_{n}=\frac{v^2}{R}\)被称为нормальное ускорение 法向加速度，
\(a_{\tau}=\frac{dv}{dt}\) 被称为 тангенциальное ускорение 切向加速度。
动力学 Динамика
| 俄文 | 中文 | 备注 |
|---|---|---|
| динамика | 动力学 | 运动学研究物体的运动轨迹，动力学研究物体为何运动 |
| сила | 力 | \([\vec{F}]=\) Н 牛顿Ньютон силы действуют на тело 力作用在物体上, уравновешивают друг друга 互相平衡 |
| давление | 压强 | |
| масса | 质量 | |
| Ⅰ закон Ньютона 可简写为 Ⅰ-й з-н Ньютона | 牛顿第一定律 | \(\sum\limits_{i=1}^{n}\vec{F_{i}}=0 \Rightarrow \frac{dv}{dt}=0\) 一切物体在没有受到外力的作用时，总保持静止状态或匀速直线运动状态。 |
| Ⅱ закон Ньютона | 牛顿第二定律 | \(\frac{d\vec{p}}{dt}=\vec{F}\) |
| Ⅲ закон Ньютона | 牛顿第三定律 | \(\vec{F}_{12}=-\vec{F}_{21}\) |
| импульс частицы | 动量 | mv |
| импульс силы | 冲量 | Ft |
| закон изменения импульса (ЗИИ) | 动量定理 | \(\Delta \vec{p}=\vec{p}_{2}-\vec{p}_{1}=\int_{t_{1}}^{t_{2}}\vec{F}dt\) |
| сила гравитационного взаимодействия | 万有引力 | \(\vec{F}=-\phi \frac{m_{1}m_{2}}{r^{2}} \frac{\vec{r}}{r}\) , где \(\phi =6,67·10^{-11} Н·М^{2}/кг^{2}\) |
| гравитационная постоянная | 万有引力常数 | \(\phi =6,67·10^{-11} Н·М^{2}/кг^{2}\) |
| гравитация | 重力 | |
| упругая сила | 弹力 | \(F_{x}=-k\Delta x\) |
| коэффициент упругости тела | 弹性系数 | k |
| удлинение пружины (стержня) | 弹簧（杆）的伸长量 | \(\Delta x\) |
| упругое напряжение | 应力 | \(\sigma=E \varepsilon=\frac{F}{S}\) |
| модуль Юнга | 杨氏模量 | \(E\) |
| сила трения | 摩擦力 | $F_{тр}=\mu N $ |
| коэффициент трения | 摩擦系数 | \(\mu\) |
| сила трения скольжения | 滑动摩擦力 | |
| статическое трение | 静摩擦力 | |
| сила нормальной реакции опоры | 支持力 | \(N\) |
| сила сопротивления | 阻力 | |
| сила сопротивления среды | 流体阻力 | \(\vec{F}=-r\vec{v}\) |
| 俄文 | 中文 | 备注 |
|---|---|---|
| механическая система (МС) | 力学系统 | |
| центр масс (ЦМ) | 质心 | |
| внешние силы | 外力 | |
| внутренние силы | 内力 | |
| замкнутая (изолированная) | МС замкнута, если на её тела не действуют внешние силы. | |
| закон сохранения импульса (ЗСИ) | 动量守恒定律 | Если \(\sum \limits_{i=1}^{n} \vec{F}_{i}^{(e)}=0\) то \(\frac{d\vec{p}_{c}}{dt}=0\) |
| момент силы | 力矩 | 与 относительно точки A 连用。 \(\vec{M}=[\vec{r},\vec{F}]\) |
| момент импульса | 角动量 | \(\vec{L}=[\vec{r},\vec{p}]\), \(\frac{d\vec{L}}{dt}=\vec{M}\) |
| момент инерций | 转动惯量 | \(J_{z}=\sum\limits_{i=1}^{n}m_{i}r_{i}^{2}\) ，\(J_{z}\varepsilon_{z}=M_{z}\) , \(L_{z}=\omega J_{z}\) |
| закон сохранения момента импульса (ЗСМИ) | 角动量守恒 | |
| Теорема Штейнера | 平行轴定理 | \(I = I_{c} + md^{2}\) |
常见物体的转动惯量
| Твёрдое тело 刚体 | расположение оси c 旋转轴的位置 | \(J_{c}\) |
|---|---|---|
| тонкий стержень длины l 长度为l的细杆 | \(\bot\)стержню 垂直于杆 | \(ml^{2}/12\) |
| сплошной цилиндр радиуса R 半径为R的实心圆柱体 | совпадает с осью цилиндра 与圆柱的轴重合 | \(mR^{2}/2\) |
| тонкий диск радиуса R 半径为R的薄盘 | совпадает с диаметром диска 与盘的直径重合 | \(mR^{2}/4\) |
| шар радиуса R 半径为R的球 | проходит через центр шара 穿过球的中心 | \(2mR^{2}/5\) |
能量与功
| 俄文 | 中文 | 备注 |
|---|---|---|
| работа | 功 | В СИ A=[Дж] 单位为焦耳 |
| энергия | 能量 | |
| элементарная работа | 功的微元 | \(\delta A = (\vec{F},d \vec{r})\) |
| мощность | 功率 | P. В СИ P=[Вт] 单位为瓦特 |
| кинетическая энергия | 动能 | \(E_{k}=\frac{mv^{2}}{2}=\frac{p^{2}}{2m}\) |
| консервативная сила | 保守力 | |
| потенциальная энергия | 势能 | \(E_{p}\) |
| неконсервативная сила | 非保守力 | 比如摩擦力等会产生热能耗散的力 |
| потенциальная энергия растянутой пружины | 弹性势能 | |
| гравитационная потенциальная энергия | 重力势能 | |
| закон сохранения полной механической энергии(ЗСМЭ) в ИСО | 机械能守恒 | |
| полная механическая энергия | 总机械能 |
波和振动 Колебание и волна
振动 Колебание
振动有好处也有坏处。 В технике колебания могут играть как положительную роль (маятник, колебательный контур и т.д.), так и отрицательную (вибрации машин и сооружений и т.д.).
| 俄文 | 中文 | |
|---|---|---|
| колебание | 振动 | |
| периодическое колебание | 周期振动 | |
| период колебаний \(T\) | 振动周期 | В СИ T =[с], |
| частота колебаний \(v=\frac{1}{T}\) | 振动频率 | В СИ ν = [Гц], [1 Гц]=[1с–1] |
| гармонические колебания | 简谐运动 | \(x=A\cos(\omega_{0}t+\alpha)\), где A - амплитуда колебаний 振幅，\((\omega_{0}t+\alpha)\) - фаза колебаний相位，\(\alpha\) - начальная фаза 初相位 |
| Дифференциальное уравнение (ДУ) гармонических колебаний | 简谐运动的微分方程 | \(\ddot{x}+\omega_{0}^{2}x=0\) 是 однородное ДУ второго порядка 齐次二阶微分方程。简谐运动的角速度就是\(\omega_{0}\) |
| круговая или циклическая частота гармонических колебаний | 圆频率或角频率 | \(\omega_{0}=\frac{2\pi}{T}=2 \pi v\) В СИ \(\omega_{0}=[c^{-1}]\) |
| когерентные колебания | 相干波 | 相位差恒定的波 это согласованные во времени и пространстве колебания, у которых разность фаз \(\Delta \Phi=\Phi_{2}-\Phi_{1}=const\) , не зависит от времени t. |
| биения | 拍 | колебания с периодически изменяющейся амплитудой. \(x=A\cos(\omega_{01}t)+A\cos(\omega_{02}t)=2A\cos (\omega_{ср}t)\cos(\omega_{мод}t)\) , где \(\omega_{ср}=\frac{\omega_{01}+\omega_{02}}{2}\) - средняя круговая частота, \(\omega_{мод}=\frac{\omega_{01}-\omega_{02}}{2}\) - круговая частота модуляции (частота биений). |
| осциллятор | 振子 | Осциллятор – система, совершающая колебания. |
| фазовая траектория | 动量p-x的轨迹。对简谐运动来说是一个椭圆。 | |
| математический маятник | 数学摆 | 一般指单摆。\(\omega=\sqrt{\frac{g}{l}}\) |
| свободное затухающее колебание | 自由衰减振动 | 微分方程为\(x''+2\beta x'+\omega_{0}^{2} x=0\), 存在阻力 сила сопротивления \(\vec{F^{c}}=-r\vec{v}\) \(x=A_{0}e^{-\beta t}\cos(\omega t+\alpha)\), где \(\omega=\sqrt{\omega_{0}^{2}-\beta^{2}}\) \(\omega_{0}=\sqrt{\frac{k}{m}}\) - собственная частота осциллятора, \(\beta=\frac{r}{2m}\) - ампкоэффициент затухания системы. литуда затухающих колебаний \(A(t)=A_{0}e^{-\beta t}\) 如果\(\omega_{0}>\beta\)， 则做Затухающие колебания运动，如果 \(\omega_{0}<\beta\)，则做Процесс релаксации，不会波动。 |
| Декремент затухания | (??) | Декремент затухания характеризует относительное уменьшение амплитуды колебаний за период. \(D=\frac{A(t)}{A(t+T)}=e^{\beta t}\) |
| Логарифмический декремент затухания | \(\lambda_{D}=\ln D\) | |
| время релаксации | \(\tau=1/\beta\) | |
| Число колебаний, совершаемых системой за время релаксации | \(N_{e}=\frac{\tau}{T}=\frac{1}{\beta t}=\frac{1}{\lambda_{D}}\) | |
| Добротность колебательной системы | \(Q=\frac{\pi}{\lambda_{D}}=\pi N_{e}\) | |
| вынужденные колебание | 受迫振动 | |
| резонанс | 共振 | |
| резонансная частота | 谐振频率 |
波 Волна
| 俄文 | 中文 | 注释 |
|---|---|---|
| волна - волны | 波 | |
| волновая поверхность | 波面 | |
| волновая поле | 波场 | |
| волновой фронт | 波前 | |
| механическая волна | 机械波 | |
| одномерная волна | 一维波 | |
| поверхностная волна | 二维波 | |
| пространственная волна | 三维波 | |
| продольная волна | 纵波 | |
| поперечная | 横波 | |
| волновое уравнение | 波函数 | \(\xi (x,t)\) |
| упругая волна | 弹性波 | |
| гармоническая волна | 简谐波 | \(\varepsilon=A\cos(t-\frac{x}{v})\) |
| обратная волна | 反向传播的波 | \(\varepsilon'=A\cos(t+\frac{x}{v})\) |
| фазовая скорость | 波速 | \(v\) 英文字母 \(v=\frac{dx}{dt}=\frac{\omega}{k}\) |
| длина волны | 波长 | \(\lambda=\frac{v}{\nu}=v T\) |
| волновое число | 波数 | \(k=\frac{2\pi}{\lambda}\) |
| 频率 | \(\nu\) 希腊字母，读作ню \(\nu=\frac{\omega}{2\pi}\) |
|
| монохроматическая волна | 单色波 | |
| объёмная плотность энергии | 能量密度 | \(w=\frac{dE}{dV}=\rho A^{2} \omega^{2} \sin^{2}(\omega t - k x)\) |
| вектор Умова | 乌莫夫矢量 | \(j=\frac{dE}{dS_{\perp}dt}\), \([j]=\frac{Дж}{М^{2}с}\) \(\vec{j}=w\vec{v}\) |
| поток энергии \(\Phi\) через производную поверхность S | 能量的流量(??) | \(\Phi=\int\limits_{S}\vec{j}d\vec{S}\) |
| когерентные волны | 相干波 | |
| интерференция волн | 波的干涉 | |
| стоячая волна | 驻波 | |
| пучность | 波腹 | |
| узел - узлы | 波节 |
狭义相对论 Специальная теория относительности (СТО)
| 俄文 | 中文 | 注释 |
|---|---|---|
| преобразование Галилея | 伽利略变换 | |
| постулаты Эйнштейна | 爱因斯坦假设 | 1. Постулат относительность 2. Постулат инвариантности скорости светв 光速不变假设 |
| преобразование Лоренца | 洛伦兹变换 | \(x'=\frac{x-ut}{\sqrt{1-(u/c)^{2}}}\), \(y'=y\), \(z'=z\) \(t'=\frac{t-(ux/c^{2})}{\sqrt{1-(u/c)^{2}}}\) |
| событие | 事件 | |
| интервал | 间隔 | \(s_{12}=c^{2}t_{12}^{2}-l_{12}^{2}=inv\) |
| типы интервалов | 间隔的类型 | 1. пространственноподобный 类空: \(l_{12}>ct_{12}\) 2. времениподобный 类时: \(l_{12}<ct_{12}\) 3. светоподобный 类光: \(l_{12}=ct_{12}\) |
| причинно-связаны | 因果关系 | |
| энергия покоя | 静能 | \(\varepsilon_{0}=m_{0}c^{2}\) |
| полная энергия частицы | 总能 | \(\varepsilon=\varepsilon_{0}+E_{k}\) |
\(m=\frac{m_{0}}{\sqrt{1-v^{2}/c^{2}}}=\gamma m_{0}\)
\(L=L_{0}\sqrt{1-v^{2}/c^{2}}\)
\(m^{2}(1-v^{2}/c^{2})=m_{0}^{2}c^{2}\)
Закон взаимосвязи массы и энергии质能关系：
\(\varepsilon^{2}-p^{2}c^{2}=m_{0}^{2}c^{4}=\varepsilon_{0}^{2}\)
то \(pc=\sqrt{E_{k}(E_{k}+2m_{0}c^{2})}\)
热力学 Термодинамика
| 俄文 | 中文 | 注释 |
|---|---|---|
| Термодинамика | 热力学 | Термодинамика — раздел физики, изучающий наиболее общие свойства макроскопических систем и способы передачи и превращения энергии в таких системах. |
| замкнутая | 封闭的 | 与环境没有热交换 |
| макросистема | 宏观系统？？ | |
| микросистема | 微观系统？？ | |
| статистическая физика | ||
| самопроизвольно | 自发地 | |
| внутренняя энергия | 内能 | U |
| передача | 传输 | |
| перенос | 转移 | |
| теплопередача | 热传导 | |
| термодинамическое равновесие | 热力学平衡 | |
| тройная точка воды | 水的三相点 | \(T_{тр}=273,16K\) |
| шкала Кельвина | 开氏温标 | |
| шкала Цельсия | 摄氏温标 | |
| 水的冰点 | \(T_{пл}=273,15K=0℃\) | |
| 水的沸点 | \(T_{к}=373,15K\) | |
| абсолютный нуль | 绝对零度 | |
| теплота | 热能 | |
| количество теплоты | 热量 | Q |
| теплообмен | 热交换 | |
| энтропия | 熵 | S |
| закон возрастания энтропии | 熵增原理 | |
| гипотезая тепловая смерть Вселенной | 宇宙热寂说 | |
| энтальпия | 焓 | H |
热力学三大定律 Начали термодинамики
-
Первое начало термодинамики: \(Q=\Delta U + A\) 热量 = 内能变化 + 对外做功。气体对外做功时，A>0
-
Второе начало термодинамики: \(dS \ge \frac{\delta Q}{T}\)
-
Третье начало термодинамики: \(\lim \limits_{T\to 0} S = 0\) 后果：绝对零度无法达到
理想气体 Идеальный газ
| 俄文 | 中文 | 注释 |
|---|---|---|
| идеальный газ | 理想气体 | |
| уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) | 理想气体状态方程 | \(pV=\frac{m}{\mu}RT=\nu RT\) \(\nu\) - количество вещества 物质的量 \(\mu\) - молярная масса газа 气体的摩尔质量 R=8,314 Дж/(моль·К) 为универсальная газовая постоянная |
| молярная масса | 摩尔质量 | 国内记作M，俄罗斯为\(\mu\) |
| количество вещества | 物质的量 | 国内记作n，俄罗斯为\(\nu\) |
| моль-моли | 摩尔 | |
| постоянная Авогадро | 阿伏伽德罗常数 | \(N_{A}=6,022\cdot 10^{23}\) моль\(^{-1}\) |
| изотермический процесс | 等温过程 | 此时有 закон Бойля-Мариотта: \(pV=const\) изотерма 等温线 |
| изобарический(изобарный) процесс | 等压过程 | 此时有 закон Гей-Люссака: \(\frac{V}{T}=const\) изобара 等压线？ |
| изохорический(изохорный) | 等体过程 | 此时有 закон Шарля: \(\frac{P}{T}=const\) изохора 等容线？ |
| теплоёмкость тела | 热容 | \(C_{T}=\frac{\delta Q}{dT}\) |
| удельная теплоёмкость | 比热容 | \(c=\frac{C_{T}}{m}\) |
| молярная теплоёмкость | 摩尔热容 | \(C=\frac{\mu}{m}=\frac{1}{\nu}\frac{\delta Q}{dT}=\frac{C_{T}}{\nu}\) |
| 定压比热容 | \(p=const: C_{p}=\frac{\delta Q}{dT}=\frac{dU}{dT}+\frac{\delta A}{dT}=\frac{i}{2}R+p\frac{dV}{dT}=\frac{i+2}{2}R\) при \(\nu=1\) \(C_{p}=\frac{i+2}{2}R\) |
|
| 定容比热容 | \(V=const: C_{V}=\frac{i}{2}R\) | |
| уравнение Майера | \(C_{p}=C_{V}+R\) | |
| адиабатический процесс | 绝热过程 | |
| уравнение Пуассона | 绝热过程中： \(pV^{\gamma}=const\) , где \(\gamma=\frac{C_p}{C_V}=\frac{i+2}{i}\) - показатель адиабаты 能推出： \(TV^{\gamma-1}=const\) |
|
| политропический(политропный) процесс | 多变过程 |  [1] |
| показатель политропы | 多变指数 | \(pV^{n}=const\) \(n=\frac{C-C_{p}}{C-C_{v}}\) \(\Rightarrow C=\frac{nC_{V}-C_{p}}{n-1}\) 中文书上这样写，做题也是这样：\(C=C_{V}-\frac{R}{n-1}\) n=0: 等压过程; n=1: 等温过程; n=\(\infin\): 等体过程; 求做功： \(A=\int \limits_{V_{1}}^{V_{2}} p\ dV = \int \limits_{V_{1}}^{V_{2}} \frac{p_{1}V_{1}^{n}}{V^{n}} dV\) |
| газ Ван-дер-Ваальса | 范德瓦尔斯气体 | \((p+\frac{a\nu^{2}}{V^{2}})(V-b\nu)=\nu RT\) |
理想气体的分子动力学理论 молекулярно-кинетической теории (МКТ) идеального газа
Основное уравнение МКТ: \(p=\frac{2}{3}n\varepsilon_{пост}=nkT\) , где \(k=1,38\cdot 10^{-23}\) Дж/К - потоянная Болбцмана 玻尔兹曼常数. \(\varepsilon_{пост}=\frac{m_{0}v_{кв}^{2}}{2}=\frac{3}{2}kT\) - средняя энергия поступательного движения молекулы.分子平移运动的平均能量
实际上\(\varepsilon = \frac{ikT}{2}\)
每个自由度的能量为\(\frac{kT}{2}\)
\(i=i_{пост.} + i_{вр.} + 2i_{кол.}\) 平移，旋转和振动的自由度
分子：
单原子одноатомной: i = 3
双原子двухатомной: i = 5
三原子 трёхатомной: i = 6
Внутренняя энергия идеального газа 理想气体的内能 $U=\nu \frac{i}{2}RT $
卡诺循环 Цикл Карно
| 俄文 | 中文 | 注释 |
|---|---|---|
| квазистатический процесс | 准静态过程 | |
| обратимый | 可逆的 | |
| необратимый | 不可逆的 | |
| цикл | 循环 | |
| поглощенное тепло - \(Q_{1}\) | 吸热 | |
| отдаваемое рабочим теплом холодильнику тепло - \(Q_{2}\) | 放热 | |
| работа за цикл | \(A=Q_{1}-Q_{2}'\) | |
| коэффициент полезного действия (КПД) | 效率 | \(\eta=\frac{A}{Q_{1}}=\frac{Q_{1}-Q_{2}'}{Q_{1}}\) Значение \(\eta=1\) запрещено вторым началом термодинамики. 对于理想气体，在卡诺循环下：\(\eta=1-\frac{T_{2}}{T_{1}}\) |
| холодильный коэффициент | 制冷系数 | \(\varepsilon=\frac{Q_{2}}{A'}=\frac{Q_{2}}{Q_{1}'-Q_{2}}\) |
| первая теорема Карно | \(\eta=1-\frac{T_{2}}{T_{1}}\) | |
| вторая теорема Карно | \(\eta_{H}<\eta_{O}\) 不可逆循环的效率比可逆循环的效率低 | |
| неравенство Клаузиуса | 克劳修斯不等式 | \(\oint \frac{\delta Q}{T}\le 0\) 可逆过程中，等号成立 |
| энтропия | 熵 | \(dS=\frac{\delta Q}{T}\) |
麦克斯韦关系 Соотношения Максвелла
| 从\(TdS=dU+PdV\)开始…… | |||
|---|---|---|---|
| \(V,S\) | \(P,S\) | \(V,T\) | \(P,T\) |
| \(dU=TdS-PdV\) | \(TdS=dU+PdV\) | \(dU-TdS=-PdV\) | \(dU-TdS+PdV=0\) |
| 转化为热力学势 | |||
| внутренняя энергия 内能 \(U=U(V,S)\) |
энтальпия 焓 \(H(P,S)=U+PV\) |
термодинамический потенциал Гельмгольца 或 свободная энергия 亥姆霍兹自由能 \(\Psi(V,T)=U-TS\) |
энергия Гиббса 吉布斯自由能 \(G(P,T)=U-TS+PV\) |
| \(T=(\frac{\part U}{\part S})_{V}\) | \(T=(\frac{\part H}{\part S})_{P}\) | \(S=-(\frac{\part \Psi}{\part T})_{V}\) | \(S=-(\frac{\part G}{\part T})_{P}\) |
| \(P=-(\frac{\part U}{\part V})_{S}\) | \(V=(\frac{\part H}{\part P})_{S}\) | \(P=-(\frac{\part \Psi}{\part V})_{T}\) | \(V=(\frac{\part G}{\part P})_{T}\) |
| 俄文 | 中文 | 注释 |
|---|---|---|
| функция состояния | 状态函数 | |
| термодинамический потенциал | 热力学势 | |
| внутренняя энергия | 内能 | \(U=U(V,S)\) |
| энтальпия | 焓 | \(H(P,S)=U+PV\) |
| термодинамический потенциал Гельмгольца 或 свободная энергия | 亥姆霍兹自由能（国内用A表示） | \(\Psi(V,T)=U-TS\) |
| энергия Гиббса | 吉布斯自由能 | \(G(P,T)=U-TS+PV\) |
| химический потенциал | 化学势 | \(\mu_{x}(P,T)=\frac{G(P,T)}{N}\) |
| удельный термодинамический потенциал | \(\varphi(P,T)=\frac{G(P,T)}{m}\) | |
| 占点位置，不然这个格子的宽度不够。 |
焦耳-汤姆生效应 Эффект Джоуля-Томпсона
（翻完了PPT截图也不知道这么多公式讲的啥）
принцип Ле Шателье - Брауна 勒夏特列原理：在一个已经达到平衡的反应中，如果改变影响平衡的条件之一（如温度、压强，以及参加反应的化学物质的浓度），平衡将向着能够减弱这种改变的方向移动。
统计物理学 Статистическая физика
| 俄文 | 中文 | 注释 |
|---|---|---|
| микрочастиц | 微粒 | 包括原子和分子 |
| барометрическая формула | 重力场中等温气压公式 | \(p=p_{0}e^{-\frac{m_{0}gz}{kT}}=p_{0}e^{-\frac{E_{p}}{kT}}\) |
| концентрация | 浓度 | \(n(x,y,z)=N_{0}f(x,y,z)\) , где \(N_{0}\) - полное число микрочастиц в объеме системы. |
| распределение Больцмана | 玻尔兹曼分布 | \(n(x,y,z)=n_{0}e^{-\frac{E_{p}(x,y,z)}{kT}}\) , где \(n_{0}\) концентрация газа в точке, соответствующей началу координат, при \(E_{p}(x,y,z)\vert _{x=y=z=0} = 0\) |
| функция распределения Максвелла | 麦克斯韦速度分布律 | \(f(v)=(\frac{m_{0}}{2\pi kT})^{\frac{3}{2}}e^{-\frac{m_{0}v^{2}}{2kT}}\) |
迁移现象 Явления переноса
气体的迁移现象 Явления переноса в газах：
-
диффузию - при переносе m, 扩散现象
-
вязкое трение в движущемся газе (вязкость газа) - при переносе p 粘滞现象
-
теплопроводность - при переносе ε. 热传导现象
общее уравнение переноса：
\(j_{G}=-\frac{1}{3}<v>n\lambda \frac{\part G}{\part x}\)
Внутреннее трение или вязкость 粘度
\(f=η\vert \frac{\part u}{\part x}\vert\)
η - коэффициент вязкости (вязкость) 粘度系数
Теплопроводность 热导率，又称导热系数
\(j_{Q}=-\frac{1}{3}<v>\rho c_{V}\frac{\part T}{\part x}\)
коэффициент теплопроводности (теплопроводность) 传热系数
\(\aleph=\frac{1}{3}<v>\lambda \rho c_{V}\)
电磁学
缩写
| 缩写 | 俄文 | 中文 |
|---|---|---|
| эл. | электрический | 电 |
| э/м. | электромагнитный | 电磁 |
| э/ст. | электростатический | 静电。比如静电场 |
电场 Электрическое поле
| 俄文 | 中文 | 注释 |
|---|---|---|
| электрический заряд(q) | 电荷 | [Кл] (кулон), 1 Кл = 1 A·c |
| элементарный электрический заряд | 单位电荷 | \(e=1,602\cdot 10^{-19}\) Кл |
| 研究带电体的两种方法： | ||
| микроскопическая теория | 微观 | \(q=\pm Ne, N=1,2,3...\) |
| макроскопическая теория | 宏观 | 把物体视为由很多粒子构成，根据电荷密度来计算 |
| линейная плотность электрического(эл.) заряда | 电荷线密度 | \(\lambda=\frac{dq}{dl}\) |
| поверхностная плотность эл. заряда | 电荷面密度 | \(\sigma=\frac{dq}{dS}\) |
| объёмная плотность эл. заряда | 电荷体密度 | \(\rho=\frac{dq}{dV}\) |
| точечный электрический заряд | 点电荷 | |
| в вакууме | 真空中 | |
| закон Кулона | 库伦定律 | \(\vec{F_{2}}=k\frac{q_{1}q_{2}}{r_{12}^{2}}\vec{e_{12}}\) , где \(k=\frac{1}{4\pi \varepsilon_{0}}=9\cdot 10 ^{9} м/\Phi,\ \vec{e_{12}}=\vec{r_{12}}/r_{12}\), где \(\varepsilon_{0}=8,85\cdot 10^{-12} \Phi / м\) |
| электрическая постоянная | 介电常数 | |
| Электрически изолированная система | система заряженных тел, которые располагаются в некотором объеме пространства, ограниченном замкнутой поверхностью, которую не пересекают заряженные частицы. | |
| Закон сохранения электрического заряда | 电荷守恒定律 | Алгебраическая сумма электрических зарядов (полный заряд) в электрически изолированной системе всегда сохраняется, т.е. не изменяется со временем. |
| пробный заряд | 试验电荷 | |
| напряженность электрического поля | 电场强度 | \(\vec{E}=\frac{\vec{F}}{q_{пр}}\) , В СИ \(\vert \vec{E} \vert = [В/м]\) \(div\ \vec{E}=\rho/\varepsilon_{0}\) \(\vec{E}=-grad \varphi = -\nabla \varphi\) |
| уравнение Пауссона | $div(grad\varphi)=\nabla^{2}\varphi=\Delta\varphi=-\frac{\rho(M)}{\varepsilon_{0}} $ | |
| элементарный поток вектора э/ст поля | 电通量 | \(\Phi_{E}=\int \limits_{S}\vec{E}d\vec{S}\) |
| потенциал | 电势 | \(\varphi\) |
| потенциал точеного заряда q | 点电荷的电势 | \(\varphi = \frac{1}{4\pi \varepsilon_{0}}\frac{q}{r}\) |
| напряжение | 电压 | U |
| электрический диполь | 电偶极子 | 电场中的电偶极子可以这样表示：\(M=[\vec{p},\vec{E}]\) 其中\(\vec{p}=q\vec{l}\) |
| заряженный | 充满电荷的 |
电介质中的电场
| 俄文 | 中文 | 注释 |
|---|---|---|
| диэлектрик | 电介质 | |
| поляризованность | 极化强度 | Для изотропного диэлектрика 对于各向同性电介质：\(\vec{P}=\kappa \varepsilon_{0}\vec{E}\), 其中\(\kappa\) 为 диэлектрическая восприимчивость 电极化率，для неполярных диэлектриков?? \(\kappa = n \beta\), n - концентрация молекул |
| вектор электрического смещения | 电位移矢量 | \(\vec{D}=\varepsilon_{0}\vec{E}+\vec{P}=\varepsilon\varepsilon_{0}\vec{E}\) B CN \(\vec{D}=[Кл/м^{2}]\) |
| теорема Гаусса | 高斯定理 | \(\oint \limits_{S} \vec{D}d\vec{S}=q\) 另一种表示方法: \(\nabla\cdot \vec{D}=\rho\) |
介质之间的电场，有\(D_{2n}=D_{1n}, E_{2\tau}=E_{1\tau}\)
电容 Ёмкость
| 俄文 | 中文 | 注释 |
|---|---|---|
| ёмкость | 电容 | В СИ С = [Ф] (фарада) 单位为法拉。 1Φ =1Кл/В. Используются: мФ, мкФ, пФ и др. |
| конденсатор | 电容器 | \(C=\frac{q}{U}\) , \(U=\vert \varphi_{1}-\varphi_{2} \vert\) |
| плоский конденсатор | 平行板电容器 | \(C=\frac{q}{U}=\frac{\varepsilon \varepsilon_{0}S}{h}\) |
| цилиндрический конденсатор | 圆柱形电容器 | \(C=\frac{2\pi \varepsilon \varepsilon_{0} h}{\ln{\frac{b}{a}}}\) |
| сферический конденсатор | 球形电容器 | \(C=\frac{4 \pi \varepsilon \varepsilon_{0}}{\frac{1}{a}-\frac{1}{b}}\) |
| система параллельно соединенных конденсаторов | 电容器并联 | \(C=\sum C_{i}\) |
| система последовательно соединенных конденсаторов | 电容器串联 | \(\frac{1}{C}=\sum \frac{1}{C_{i}}\) |
| энергия системы неподвижных зарядов | 静电荷系统的能量 | \(W_{p\ ik}=\frac{1}{4\pi \varepsilon_{0}}\frac{q_{i}q_{k}}{r_{ik}}\) |
| энергия конденсатора | 电容的能量 | \(W_{p}=\frac{CU^{2}}{2}\) |
磁场 Магнитное поле
| 俄文 | 中文 | 注释 |
|---|---|---|
| магнитное поле | 磁场 | |
| вектор магнитной индукции | 磁感应强度 | \(\vec{B}\), в си B = [Тл] (тесла) 单位为特斯拉 有\(\vec{B}=\mu_{0}\vec{H}\) , где \(\mu_{0}=1,257\cdot 10^{-6}\) Гн/м |
| вектор напряженности магнитного поля в вакууме | 真空中磁场强度 | \(\vec{H}\), В СИ H=[А/м] |
| магнитная проницаемость | 磁导率 | |
| закон Био-Савара | 毕奥-萨伐尔定律 | \(d\vec{H}=\frac{1}{4\pi}\frac{I[d\vec{l},\vec{r}]}{r^{3}}\) 方括号框住表示叉乘 |
| магнитное поле прямого тока | 无限长直导线的磁场 | \(H=\frac{I}{2\pi b}\) |
| Магнитное поле кругового тока | 环形电流的磁场 | \(H=\frac{IR^{2}}{2(R^{2}+L^{2})^{3/2}}\) |
| теорема о циркуляции вектора индукции магнитного поля | 真空中的磁场的环路定理 | \(\oint \limits_{L} \vec{B}d\vec{l}=\mu_{0}\sum I_{i}\) \(\oint \limits_{L} \vec{H}d\vec{l}=\sum I_{i}\) |
| 磁场的高斯定理 | 磁场中通过任意封闭曲面的磁通量为零。\(\oint \vec{B}\ d\vec{S}=0\) |
物质中的磁场
| 俄文 | 中文 | 注释 |
|---|---|---|
| магнетик | 磁性 | Магнетики можно разделить на слабомагнитные 弱磁 (парамагнетики и диамагнетики) и силъномагнитные强磁 (ферромагнетики). |
| намагничивание | 磁化 | Намагничивание — приобретение веществом (его атомами и молекулами) магнитного момента. |
| магнитный момент | 磁偶极矩 | \(P_{m}=i'_{пов}\Delta S = i'\Delta l \Delta S = i'\Delta V=\sum \limits_{\Delta V}\vec{p_{m}}=J\Delta V\) 其中 \(i'_{пов}\) 为表面电流强度 |
| намагниченность | 磁极化强度 | \(J=\frac{P_{m}}{\Delta V}=i'\) \(B'=\mu_{0}i'=\mu_{0}J\) |
| 磁介质中的环路定理 | \(\oint \limits_{L} \vec{H}d\vec{l}=\sum I_{i}\) | |
| диамагнетик | 抗磁质 | 磁导率 \(\mu=\mu_{0}\mu_{r}<1\) : медь(Cu), ртуть(Hg) 等一小部分物质 \(\vec{J}=0\) при \(\vec{B_{0}}=0\) при \(\vec{B_{0}}\ne 0\) , \(\vec{p_{m}} \uparrow \downarrow \vec{B_{0}}\) 平行且方向相反 |
| парамагнетик | 顺磁质 | \(\mu>1\): калий(K), натрий(Na) 等许多物质 \(\vec{B_{0}}=0 \rightarrow \vec{p_{m}}=\sum \limits_{1}^{z} \vec{p_{o}}+\sum \limits_{1}^{z} \vec{p_{s}} \ne 0\) 在没有外部磁场的情况下，其原子（分子）有一个磁矩，但由于磁矩方向混乱，所以\(\vec{J}=0\) при \(\vec{B_{0}}\ne 0\) , \(\vec{p_{m}} \uparrow \uparrow {B_{0}}\) 平行且方向相同 |
在两个磁介质的界面上， 由高斯定理和环路定理，有 \(B_{1n}=B_{2n}\)，\(H_{1\tau}=H_{2\tau}\)
铁磁质 Ферромагнетик
J随H增长而非线性增长，直到饱和，饱和时的\(J_{нас}\) 被称为намагниченность насыщения.
\(B=\mu_{0}(H+J)\)
| 俄文 | 中文 | 注释 |
|---|---|---|
| ферромагнетик | 铁磁质 | железо (Fe), кобальт (Со), никель (Ni) |
| домен | 磁畴 | |
| гистерезис | 磁滞 | |
| остаточная индукцмя | 剩磁感应强度或剩磁 | |
| Точка Кюри (температура Кюри) | 居里点（居里温度） | 铁磁体的磁性消失的温度 |
磁场中的导体
| 俄文 | 中文 | 注释 |
|---|---|---|
| закон Ампера | 安培定则 | \(d\vec{F}=Id\vec{l} \times \vec{B}\) |
| ток | 电流 | |
| сонаправленные токи притягиваются | 同向电流相互吸引 | |
| противоположно направленные - отталкиваются. | 反向电流相互排斥 | |
| магнитный поток | 磁通量 | \(\Phi\) |
| работа амперовых сил | 安培力做功 | \(A=I\Delta \Phi\) |
带电粒子在电场和磁场中的运动
| 俄文 | 中文 | 注释 |
|---|---|---|
| обобщенная сила Лоренца | 广义洛伦兹力 | 作用在电荷q上的总电磁力 |
| магнитная сила Лоренца | （我们所学的）洛伦兹力 | \(\vec{F_{M}}=q[\vec{v},\vec{B}]\) |
| \(R=\frac{mv}{qB}\) \(T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\) |
||
| циклотрон | 回旋加速器 | Ионы будут ускоряться внешним высокочастотным электрическим полем, если частота его изменения совпадает с частотой обращения частицы (ионов) по окружности.如果外部高频电场的变化频率与粒子（离子）绕行的频率相吻合，则粒子将被外部高频电场加速。即电源周期等于粒子绕行周期：\(T=\frac{2\pi m}{qB}\) |
| 每绕半圈，粒子获得\(qU\)动能。最大速度取决于半径。 |
霍尔效应 Эффект Холла
磁场中的通电导体中的电子，受到磁场的影响，会在导体两侧产生电场。
设电场强度为\(\vec{E_{x}}\)，则\(e<\vec{v}> \times \vec{B}=-e\vec{E_{x}}\)
即 \(\vec{E_{x}}=-<\vec{v}>\times \vec{B}=-R_{x}\cdot \vec{j} \times \vec{B}\), здесь \(\vec{j}=n_{e}e<\vec{v}>\) , \(R_{x}=\frac{1}{en_{e}}\) 其中 \(n_{e}\) концентрация электронов, \(R_{x}\) постоянная Холла
霍尔效应使我们能够确定半导体电荷载体的符号（p/n）:
П/п p-типа (основные носители заряда - дырки).
p型（主要电荷载体是空穴）。
П/п и-типа (основные носители заряда - электроны).
n型（主要电荷载体是电子）。
拉莫尔进动 Ларморова прецессия
\(I=e\nu\) 这里不是v 是希腊字母\(\nu\) ，读作nu。为 частота обращения электрона вокруг ядра，为电子围绕原子核轨道的频率。
Орбитальный магнитный момент электрона电子的轨道磁矩： \(p_{m}=IS=e\nu S=e\nu \pi r^{2}\)
момент импульса и угловая скорость角动量和角速度：
\(L=m\omega r^{2}\), \(\omega = 2\pi \nu\)
гиромагнитное отношение \(\Gamma = \frac{\vec{p_{m}}}{\vec{L}}=-\frac{e}{2m}\)
сила Кориолиса 科里奥利力
Теорема Лармора: действие магнитного поля на движущийся электрон заключается в начожении на первоначальное движение равномерного вращения вокруг направления внешнего магнитного поля.
电磁场的麦克斯韦方程УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Основные положения электромагнитной теории Максвелла
-
Всякое изменение магнитного поля порождает появление в окружающем пространстве вихревого электрического поля.
-
Всякое изменение электрического поля порождает появление в окружающем пространстве магнитного поля.
麦克斯韦电磁理论的基本陈述
-
磁场的任何变化都会在周围空间产生涡流电场。
-
电场的任何变化都会在周围空间产生磁场。
Закон э/м индукции 电磁感应定律
в интегральной форме 积分形式：
\(\oint \vec{E}(\vec{r},t)d\vec{l}=-\int\limits_{s}\frac{\part \vec{B}}{\part t}d\vec{S}\)
в дифференциальной форме 微分形式：
\(rot \vec{E}(\vec{r},t)=-\frac{\part \vec{B}}{\part t}\)
ток смещения 位移电流
ток проводимости 传导电流
考虑给一个电容器充电的过程。交变电场的存在使得闭合回路得以实现。
\(I=\int\limits_{S_{1}} \vec{j}d\vec{S_{1}}\)
\(\vec{j_{см}}=\frac{\part \vec{D}}{\part t}\)
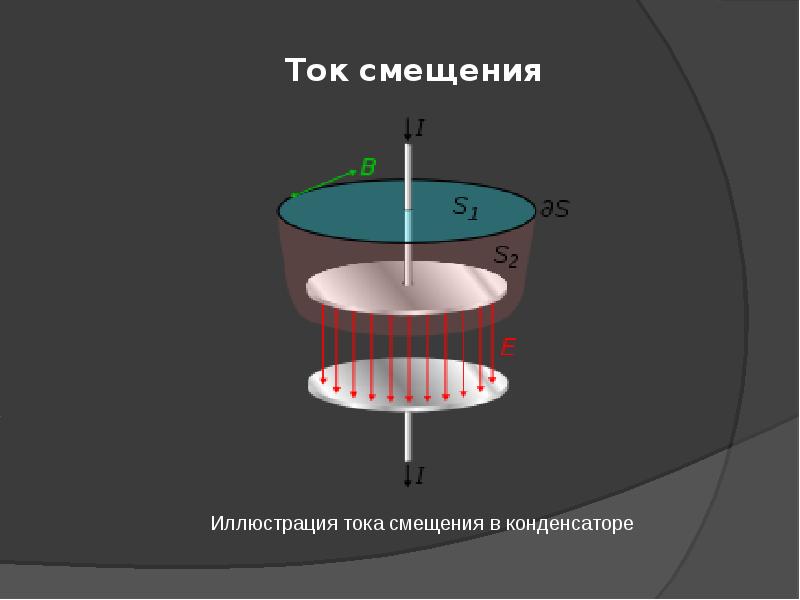
Закон полного тока 全电流定律
\(I_{полн} = I + I _{см}\), где \(I\) - ток проводимости 传导电流, \(I_{см}\) - ток смещения 位移电流
В проводнике 导体中: \(I_{см}\approx 0\) , \(I_{полн}\approx I\)
В диэлектрике 电介质中: \(I\approx 0\) , \(I_{полн}\approx I_{см}\)
в интегральной форме 积分形式：
\(\oint \limits_{\Gamma} \vec{H}d\vec{l}=\int \limits_{S} \vec{j}d\vec{S}+\int\limits_{S}\frac{\part \vec{D}}{\part t} d\vec{S}\)
в дифференциальной форме 微分形式：
\(rot \vec{H}=\vec{j}+\frac{\part \vec{D}}{\part t}\)
Уравнения Максвелла 麦克斯韦方程
в неподвижных средах (система фундаментальных ур-ий электродинамики)
в интегральной форме 积分形式：
\(\oint \limits_{\Gamma}\vec{E}d\vec{l}=-\int \limits_{S} \frac{\part \vec{B}}{\part t}d \vec{S}\)
\(\oint \limits_{S}\vec{D}d\vec{S}=\int \limits_{V} \rho dV\)
\(\oint \limits_{\Gamma} \vec{H}d\vec{l}=\int \limits_{S} \vec{j}d\vec{S}+\int\limits_{S}\frac{\part \vec{D}}{\part t} d\vec{S}\)
\(\oint \limits_{S}\vec{B}d\vec{S}=0\)
对封闭区域的积分中，S是闭合曲面，\(\Gamma\) 是闭合环路。
j是传导电流密度。
в дифференциальной форме 微分形式：
\(rot\ \vec{E}=-\frac{\part \vec{B}}{\part t}\)
\(div\ \vec{D}=\rho\)
\(rot\ \vec{H}=\vec{j}+\frac{\part \vec{D}}{\part t}\)
\(div\ \vec{B}=0\)
微分形式的另一种写法：
\(\begin{cases} \nabla\times\vec{E}=-\frac{\partial\vec{B}}{\partial t}\\ \nabla\times\vec{H}=\vec{J_v}+\frac{\partial\vec{D}}{\partial t}\\ \nabla\cdot\vec{D}=\rho_v\\ \nabla\cdot\vec{B}=0 \end{cases}\quad \begin{cases} \vec{D}=\varepsilon\vec{E}\\ \vec{B}=\mu\vec{H}\\ \vec{J_v}=\sigma\vec{E} \end{cases}\)
\(\sigma\) 是电导率。
电磁波
波动方程 волновое уравнение \(\Delta f = \frac{1}{v} \frac{\part^{2}f}{\part t^{2}}\)
即\(\frac{\part^{2}f}{\part x^{2}}+\frac{\part^{2}f}{\part y^{2}}+\frac{\part^{2}f}{\part z^{2}}= \frac{1}{v} \frac{\part^{2}f}{\part t^{2}}\)
э/м волна переносит энергию. 电磁波携带能量
Скорости э/м волны в вакууме 真空中电磁波的传播速度：
\(v_{0}=\frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}=c\)
Фазовая скорость э/м волны в среде 介质中电磁波的相速度：
\(v=\frac{1}{\sqrt{\varepsilon_{0}\mu_{0}\varepsilon\mu}}=\frac{c}{n}\)
где n - показатель преломления среды 介质的折射率 \(n=\sqrt{\varepsilon\mu}\)
坡印亭矢量 Вектор Пойнтинга (в упругой волне -вектор Умова 在弹性波中被称为乌莫夫矢量 ？？？)
\(\vec{S}=w\vec{v}=\vec{E}\times \vec{H}\)
Объемная плотность энергии э/м волны 电磁波的能量体密度\(w=w_{э}+w_{м}=\frac{\varepsilon_{0}\varepsilon E^{2}}{2}+\frac{\mu_{0}\mu H^{2}}{2}\)
光学оптика
Волновая оптика 波动光学 изучает широкий круг закономерностей, связанных с процессами распространения света в материальных средах с учетом его волновой природы.
К ней относятся: интерференция света, дифракция света, голография, поляризация света, дисперсия света. 其中包括干涉、衍射、全息、偏振和色散
Физическая оптика 物理光学- наука о природе света и световых явлений. 是研究光的性质和光现象的科学。
Геометрическая оптика 几何光学
电磁波的种类
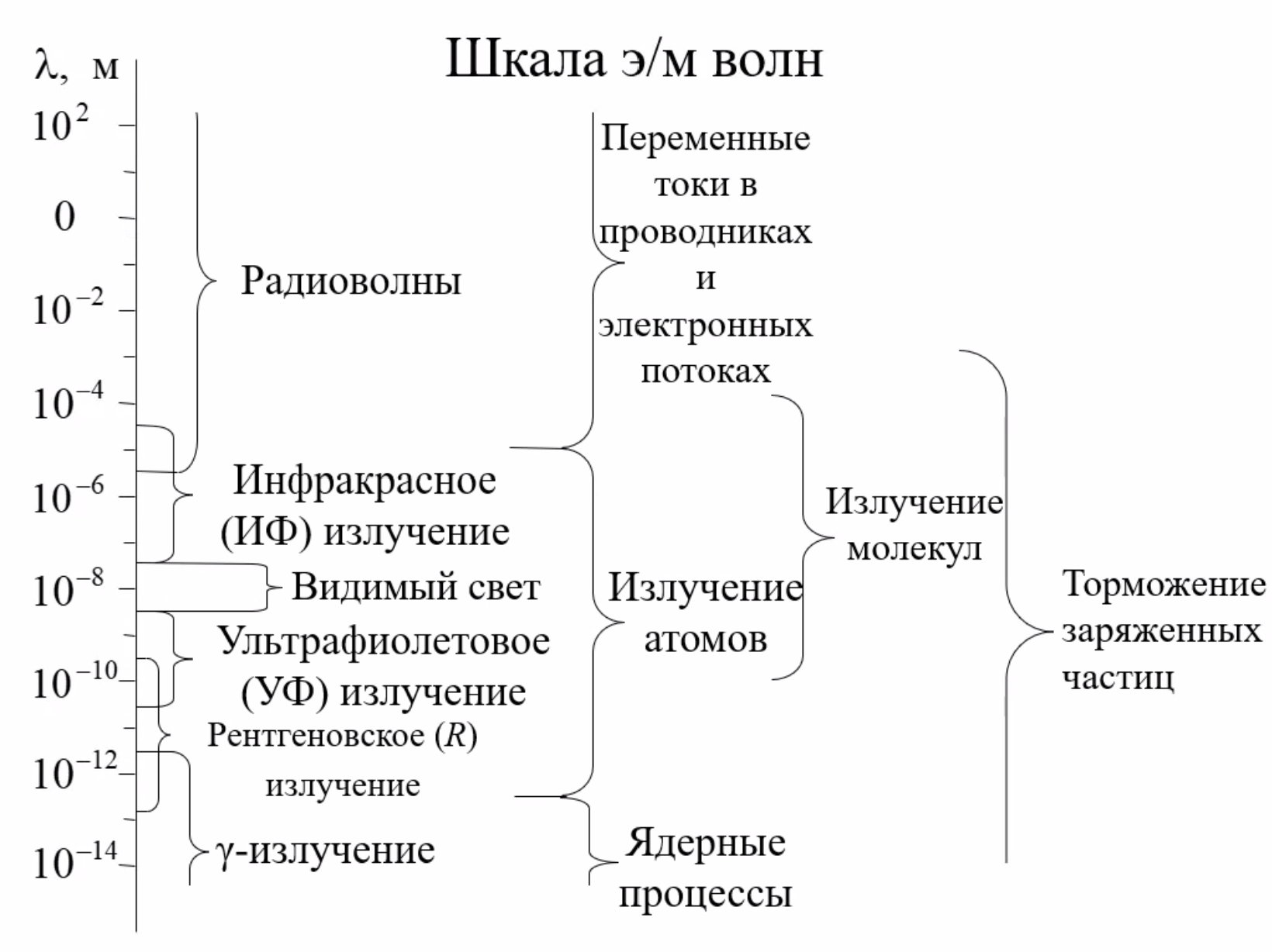
Границы диапазона видимого света определяются способностью среднестатистического человеческого глаза регистрировать э/м излучение в интервале λ = 380 ~ 780 нм. 可见光的波长范围在 λ = 380 ~ 780 纳米之间。
Интенсивность света 光强 - модуль среднего по времени значения ь плотности потока электромагнитной энергии
\(I=\frac{1}{T}\int \limits_{0}^{T} Sdt = <S>\sim E_{m}H_{m}=nE_{m}^{2}=nA^{2}\)
\(E_{m}=A\) - амплитуда светового вектора.
Интерференция электромагнитных волн 电磁波的干涉
Монохроматическая волна имеет определенную частоту. 一个单色波有一个特定的频率。
Когерентный 相干。是指两个波频率相同，相位差恒定。
принцип суперпозиции 叠加原理 \(I = I_{1}+I_{2}+2\sqrt{I_{1}I_{2}}\cos \Delta \alpha\)
参考文献 Список используемой литературы
- https://baike.baidu.com/item/多变过程/5753028
- 老师指定热力学教材：Глаголев К.В., Морозов А.Н. Физическая термодинамика.
本文来自博客园，作者：mariocanfly，转载请注明原文链接：https://www.cnblogs.com/mariocanfly/p/14500325.html
