1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts (M)
Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts (M)
题目
Given a rectangular cake with height h and width w, and two arrays of integers horizontalCuts and verticalCuts where horizontalCuts[i] is the distance from the top of the rectangular cake to the ith horizontal cut and similarly, verticalCuts[j] is the distance from the left of the rectangular cake to the jth vertical cut.
Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a huge number, return this modulo 10^9 + 7.
Example 1:
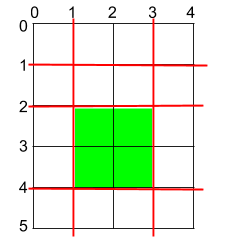
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
Output: 4
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
Example 2:

Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
Output: 6
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
Example 3:
Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
Output: 9
Constraints:
2 <= h, w <= 10^91 <= horizontalCuts.length < min(h, 10^5)1 <= verticalCuts.length < min(w, 10^5)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- It is guaranteed that all elements in
horizontalCutsare distinct. - It is guaranteed that all elements in
verticalCutsare distinct.
题意
在一个矩形上竖着和横着各切若干刀,求能得到的最大面积的小矩形。
思路
分别求出纵向和横向最大的间隔,相乘即是最大面积,注意越界。
代码实现
Java
class Solution {
public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
Arrays.sort(horizontalCuts);
Arrays.sort(verticalCuts);
int height = h - horizontalCuts[horizontalCuts.length - 1];
int width = w - verticalCuts[verticalCuts.length - 1];
int pre = 0;
for (int num : horizontalCuts) {
height = Math.max(height, num - pre);
pre = num;
}
pre = 0;
for (int num : verticalCuts) {
width = Math.max(width, num - pre);
pre = num;
}
return (int)((long) height * width % 1000000007);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号