1463. Cherry Pickup II (H)

Cherry Pickup II (H)

题目

Given a rows x cols matrix grid representing a field of cherries. Each cell in grid represents the number of cherries that you can collect.

You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.

Return the maximum number of cherries collection using both robots by following the rules below:

• From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
• When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
• When both robots stay on the same cell, only one of them takes the cherries.
• Both robots cannot move outside of the grid at any moment.
• Both robots should reach the bottom row in the grid.

Example 1:

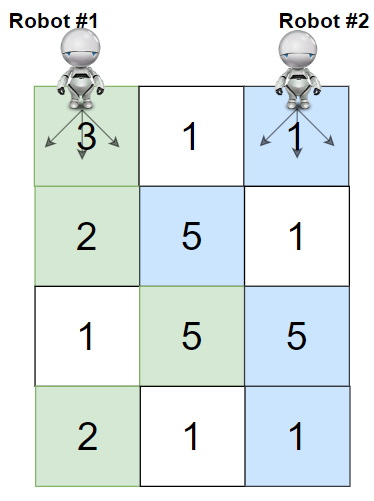
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.

Example 2:

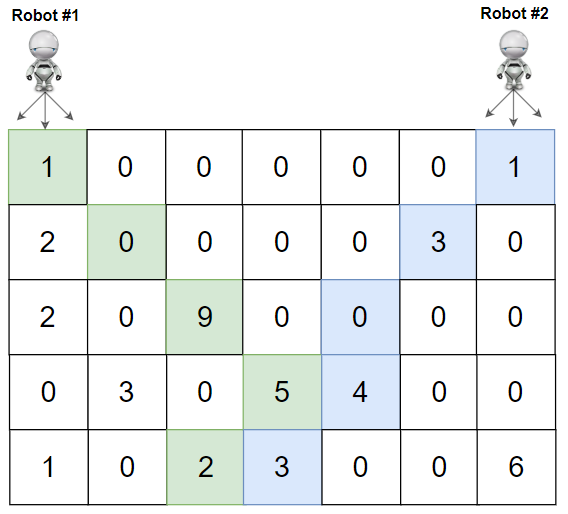
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.

Example 3:

Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
Output: 22

Example 4:

Input: grid = [[1,1],[1,1]]
Output: 4

Constraints:

• rows == grid.length
• cols == grid[i].length
• 2 <= rows, cols <= 70
• 0 <= grid[i][j] <= 100

---

题意

给定一个二维数组，两个机器人分别放在左上角和右上角，每次只能向下走一行，且位置最多只能改变一列，求路径上所有数字之和的最大值(两机器人重合时只计算一次所在数字)。

思路

动态规划。记dp[row][x][y]为在第row行，且两机器人分别在该行x列和y列时得到的最大和。而要走到(row, x, y)这个位置，上一行的位置只会有9个可能：(row - 1, x - 1 ~ x + 1, y - 1 ~ y + 1)。所以只要计算这9个位置中的最大值，再加上当前位置对应的数字，就能得到dp[row][x][y]。递推式:

\[dp[row][x][y]= \begin{cases} \begin{align} &\max_{-1 \le d_x \le 1, -1 \le d_y \le 1}(dp[row-1][x+d_x][y+d_y])\ +\ grid[row][x]\ +\ grid[row][y],&x\ne y\\ &\max_{-1 \le d_x \le 1, -1 \le d_y \le 1}(dp[row-1][x+d_x][y+d_y])\ +\ grid[row][x],&x=y \end{align} \end{cases} \]

可以用滚动数组优化，只需要记录2行的数据。

---

代码实现

Java

public class Solution {
    public int cherryPickup(int[][] grid) {
        int ans = 0;
        int len = grid[0].length;
        Integer[][][] dp = new Integer[2][len][len];		// null即为不可达
        dp[0][0][len - 1] = grid[0][0] + grid[0][len - 1];

        for (int row = 1; row < grid.length; row++) {
            int curRow = row % 2, preRow = (row + 1) % 2;
            for (int x = 0; x < len; x++) {
                for (int y = 0; y < len; y++) {
                    Integer max = null;
                    for (int i = -1; i <=1 ; i++) {
                        for (int j = -1; j <= 1; j++) {
                            if (x + i < len && x + i >= 0 && y + j < len && y + j >= 0 && dp[preRow][x + i][y + j] != null) {
                                max = max == null ? dp[preRow][x + i][y + j] : Math.max(max, dp[preRow][x + i][y + j]);
                            }
                        }
                    }
                  	// 注意当前位置可能是不可达的
                    dp[curRow][x][y] = max == null ? null : max + grid[row][x] + (x == y ? 0 : grid[row][y]);
                    
                    if (dp[curRow][x][y] != null) {
                        ans = Math.max(ans, dp[curRow][x][y]);
                    }
                }
            }
        }

        return ans;
    }
}