0987. Vertical Order Traversal of a Binary Tree (M)

Vertical Order Traversal of a Binary Tree (M)

题目

Given a binary tree, return the vertical order traversal of its nodes values.

For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).

Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).

If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.

Return an list of non-empty reports in order of X coordinate. Every report will have a list of values of nodes.

Example 1:

Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation: 
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).

Example 2:

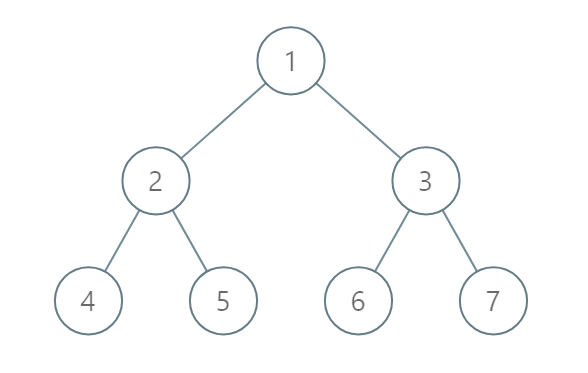
Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation: 
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.

Note:

1. The tree will have between 1 and 1000 nodes.
2. Each node's value will be between 0 and 1000.

---

题意

定义二叉树中一个结点的横坐标为x，纵坐标为y，则其左子结点坐标为(x-1, y-1)，其右子结点坐标为(x+1, y-1)，求该二叉树的纵向遍历，类似于层序遍历，x相同的结点属于同一层，不同层按x升序排列，同一层结点按y降序排列。

思路

层序遍历所有结点，这样可以保证y值是递减的；结点的x轴信息可以用一个与层序遍历同步的队列来记录；最终结果可以用一个(x->List)的map保存。注意同一层x值相同的两个结点需要按照值大小排列，因此每一层可以再开一个map进行处理，再合并到结果map中。

---

代码实现

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        List<List<Integer>> ans = new ArrayList<>();
        Map<Integer, List<Integer>> hash = new TreeMap<>();
        Map<Integer, Set<Integer>> tmp = new HashMap<>();
        Queue<TreeNode> q = new LinkedList<>();
        Queue<Integer> coord = new LinkedList<>();

        if (root != null) {
            q.offer(root);
            coord.offer(0);
        }
      
        while (!q.isEmpty()) {
            int size = q.size();
            tmp.clear();
          
            for (int i = 0; i < size; i++) {
                TreeNode cur = q.poll();
                int x = coord.poll();
                tmp.putIfAbsent(x, new TreeSet<>());
                tmp.get(x).add(cur.val);
              
                if (cur.left != null) {
                    q.offer(cur.left);
                    coord.offer(x - 1);
                }
                if (cur.right != null) {
                    q.offer(cur.right);
                    coord.offer(x + 1);
                }
            }
          
            for (int x : tmp.keySet()) {
                hash.putIfAbsent(x, new ArrayList());
                hash.get(x).addAll(tmp.get(x));
            }
        }
        for (List<Integer> list : hash.values()) {
            ans.add(list);
        }
        return ans;
    }
}

JavaScript

/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var verticalTraversal = function (root) {
  const xList = new Map()
  const q = []
  const x = []
  q.push(root)
  x.push(0)

  while (q.length) {
    const size = q.length
    const tmp = new Map()
    for (let i = 0; i < size; i++) {
      const cur = q.shift()
      const curX = x.shift()
      !tmp.has(curX) && tmp.set(curX, [])
      tmp.get(curX).push(cur.val)

      if (cur.left) {
        q.push(cur.left)
        x.push(curX - 1)
      }
      if (cur.right) {
        q.push(cur.right)
        x.push(curX + 1)
      }
    }

    for (const [key, value] of tmp.entries()) {
      value.sort((a, b) => a - b)
      !xList.has(key) && xList.set(key, [])
      xList.get(key).push(...value)
    }
  }

  return Array.from(xList.keys())
    .sort((a, b) => a - b)
    .map(key => xList.get(key))
}