通用函数

数组的裁剪

# 将调用数组中小于和大于下限和上限的元素替换为下限和上限，返回裁剪后的数组，调
# 用数组保持不变。
ndarray.clip(min=下限, max=上限)

数组的压缩

# 返回由调用数组中满足条件的元素组成的新数组。
ndarray.compress(条件)

数组的累乘

# 返回调用数组中所有元素的乘积——累乘。
ndarray.prod()
# 返回调用数组中所有元素执行累乘的过程数组。
ndarray.cumprod()

 

import numpy as np
a = np.array([10, 20, 30, 40, 50])
print(a)#[10 20 30 40 50]
#数组的裁剪
b = a.clip(min=15, max=45)
print(b)#[15 20 30 40 45]
#数组的压缩
c = a.compress((15 <= a) & (a <= 45))
print(c)#[20 30 40]

加法/乘法通用函数

np.add(a, a)                     # 两数组相加
np.add.reduce(a)                 # a数组元素累加和
np.add.accumulate(a)             # 累加和过程
np.add.outer([10, 20, 30], a)    # 外和
# 返回调用数组中所有元素的乘积——累乘。
ndarray.prod()
# 返回调用数组中所有元素执行累乘的过程数组。
ndarray.cumprod()
np.outer() #外积

案例

#加发,乘法通用函数
import numpy as np
a = np.arange(1,7)
print(a)#[1 2 3 4 5 6]
#两数组相加
print(np.add(a,a))#[ 2  4  6  8 10 12]
#数组元素累加和
print(np.add.reduce(a))#21
#累加和过程
print(np.add.accumulate(a))#[ 1  3  6 10 15 21]
#外和
print(np.add.outer([10,20,30],a))
"""
[[11 12 13 14 15 16]
 [21 22 23 24 25 26]
 [31 32 33 34 35 36]]
"""
#累乘
print(a.prod())#720
#累乘的过程
print(a.cumprod())#[  1   2   6  24 120 720]
#外乘
print(np.outer([10,20,30],a))
"""
[[ 10  20  30  40  50  60]
 [ 20  40  60  80 100 120]
 [ 30  60  90 120 150 180]]
"""

除法通用函数

np.true_divide(a, b)     # a 真除 b  （对应位置相除）
np.divide(a, b)         # a 真除 b
np.floor_divide(a, b)    # a 地板除 b    （真除的结果向下取整）
np.ceil(a / b)         # a 天花板除 b    （真除的结果向上取整）
np.trunc(a / b)            # a 截断除 b    （真除的结果直接干掉小数部分）

案例：

import numpy as np

a = np.array([20, 20, -20, -20])
b = np.array([3, -3, 6, -6])
# 真除
c = np.true_divide(a, b)
c = np.divide(a, b)
c = a / b
print('array:',c)
#array: [ 6.66666667 -6.66666667 -3.33333333  3.33333333]

# 对ndarray做floor操作
d = np.floor(a / b)
print('floor_divide:',d)
#floor_divide: [ 6. -7. -4.  3.]

# 对ndarray做ceil操作
e = np.ceil(a / b)
print('ceil ndarray:',e)
#ceil ndarray: [ 7. -6. -3.  4.]

# 对ndarray做trunc操作
f = np.trunc(a / b)
print('trunc ndarray:',f)
#trunc ndarray: [ 6. -6. -3.  3.]

# 对ndarray做around操作
g = np.around(a / b)
print('around ndarray:',g)
#around ndarray: [ 7. -7. -3.  3.]

三角函数通用函数

numpy.sin()

一个方波由如下参数的正弦波叠加而成：

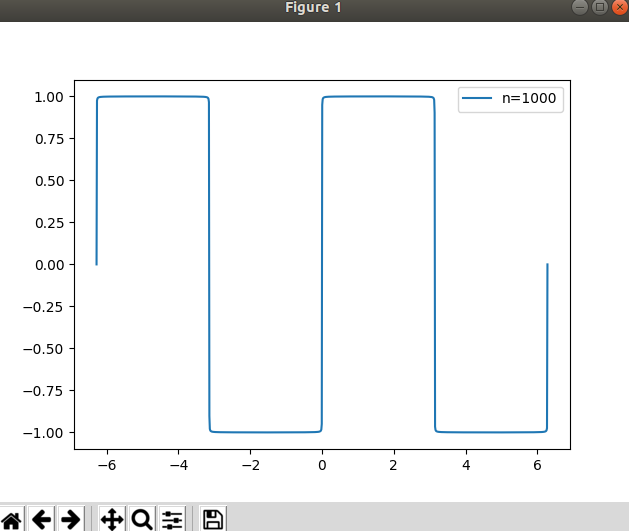
曲线叠加的越多，越接近方波。所以可以设计一个函数，接收曲线的数量n作为参数，返回一个矢量函数，该函数可以接收x坐标数组，返回n个正弦波叠加得到的y坐标数组。

x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y = np.zeros(1000)
n = 1000
for i in range(1， n+1):
    y += 4 / ((2 * i - 1) * np.pi) * np.sin((2 * i - 1) * x)
mp.plot(x, y, label='n=1000')
mp.legend()
mp.show()

 

"""
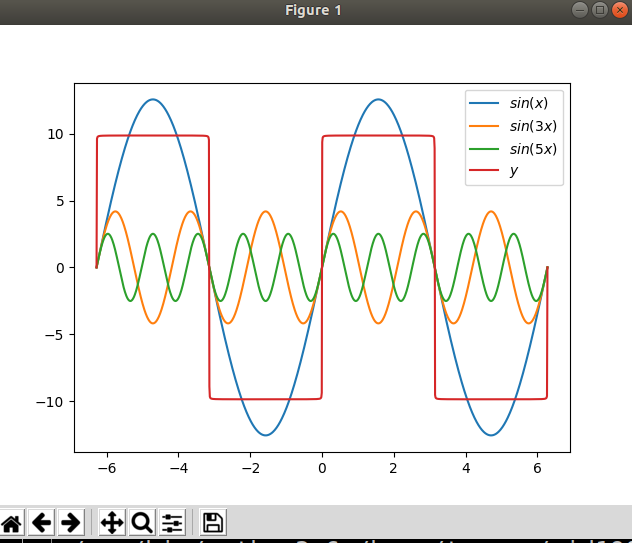
 合成方波
"""
import numpy as np
import matplotlib.pyplot as mp

x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y1 = 4*np.pi * np.sin(x)
y2 = 4*np.pi/3 * np.sin(3*x)
y3 = 4*np.pi/5 * np.sin(5*x)
y = np.zeros(x.size)
for i in range(1, 1000):
    y += 4*np.pi/(2*i-1) * np.sin((2*i-1)*x)

# mp.plot(x, y1, label=r'$sin(x)$')
# mp.plot(x, y2, label=r'$sin(3x)$')
# mp.plot(x, y3, label=r'$sin(5x)$')
mp.plot(x, y, label=r'$y$')
mp.legend()
mp.show()

位运算通用函数

位异或：

c = a ^ b
c = a.__xor__(b)
c = np.bitwise_xor(a, b)

按位异或操作可以很方便的判断两个数据是否同号。

0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0

 

a = np.array([0, -1, 2, -3, 4, -5])
b = np.array([0, 1, 2, 3, 4, 5])
print(a, b)
c = a ^ b
# c = a.__xor__(b)
# c = np.bitwise_xor(a, b)
print(np.where(c < 0)[0])
#[1 3 5]

位与：

e = a & b
e = a.__and__(b)
e = np.bitwise_and(a, b)

 

0 & 0 = 0 
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1

利用位与运算计算某个数字是否是2的幂

#  1 2^0 00001   0 00000
#  2 2^1 00010   1 00001
#  4 2^2 00100   3 00011
#  8 2^3 01000   7 00111
# 16 2^4 10000  15 01111
# ...

d = np.arange(1, 21)
print(d)
e = d & (d - 1)
e = d.__and__(d - 1)
e = np.bitwise_and(d, d - 1)
print(e)

位或：

|
__or__
bitwise_or

0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1

位反：

~
__not__
bitwise_not

~0 = 1

~1 = 0

移位：

<<        __lshift__        left_shift
>>        __rshift__        right_shift

左移1位相当于乘2，右移1位相当于除2。

d = np.arange(1, 21)
print(d)
# f = d << 1
# f = d.__lshift__(1)
f = np.left_shift(d, 1)
print(f)